- Die Originalvariante
- Das Ziegenproblem mit mehr als 3 Türen
- Das Ziegenproblem mit mehreren Moderatoren
3 Das Ziegenproblem 
3.1 Die Originalvariante
Vor einigen Jahren lief im amerikanischen Fernsehen eine Spielshow mit etwa dem folgenden Ablauf:
- Ein Kandidat steht vor drei verschlossenen Türen. Hinter einer Tür steht der vom Kandidaten erstrebte Gewinn, ein Auto, hinter den beiden anderen Türen je eine Ziege. Der Moderator bittet den Kandidaten, eine Tür zu auswählen, was dieser in Erwartung des Preises gerne tut. Die gewählte Tür bleibt aber vorerst geschlossen. Nun zeigt der Moderator, der weiß, hinter welcher Tür sich das Auto befindet, mit den Worten „Ich zeig` Ihnen `mal `was“ auf eine andere Tür und öffnet sie. Dahinter steht eine Ziege. Es gibt nun nur noch zwei verschlossene Türen, die vom Kandidaten gewählte und eine weitere. Dem Kandidaten wird nunmehr die entscheidende Frage gestellt: „Bleiben Sie bei Ihrer Wahl oder möchten Sie doch lieber zur anderen Tür wechseln?“
Die Entscheidungssituation des Kandidaten ist einigermaßen klar: es gibt zwei verschlossene Türen, hinter einer Tür steht eine Ziege, hinter der anderen ein Auto. Offenbar ist die Chance, den Gewinn zu bekommen bei beiden Türen gleich. Warum also wechseln? Dafür scheint es keinen Grund zu geben. Ein Trugschluss! Kandidaten, die wechseln, haben doppelt so hohe Gewinnchancen.
Schauen wie uns die Sache einmal genauer an. Es gibt drei Türen, aber nur einen Gewinn. Die Chance, mit der ersten Auswahl auf die Tür mit dem Auto zu tippen ist daher ![]() . Das ist folglich auch die Gewinnchance des Kandidaten, wenn er bei seiner ursprünglich gewählten Tür bleibt. Dagegen befindet sich der Hauptgewinn mit der Wahrscheinlichkeit
. Das ist folglich auch die Gewinnchance des Kandidaten, wenn er bei seiner ursprünglich gewählten Tür bleibt. Dagegen befindet sich der Hauptgewinn mit der Wahrscheinlichkeit ![]() hinter einer der beiden Türen, die der Kandidat nicht gewählt hat. Der Moderator öffnet nun aber mit Sicherheit eine Tür mit einer Ziege. Deswegen ist das Auto mit der Chance
hinter einer der beiden Türen, die der Kandidat nicht gewählt hat. Der Moderator öffnet nun aber mit Sicherheit eine Tür mit einer Ziege. Deswegen ist das Auto mit der Chance ![]() hinter der anderen Tür. Wechselt daher der Kandidat, so vergrößert er damit seine Gewinnchance von
hinter der anderen Tür. Wechselt daher der Kandidat, so vergrößert er damit seine Gewinnchance von ![]() auf
auf ![]() .
.
Eigentlich ist damit alles gesagt. Indessen, wer mit Wahrscheinlichkeiten nicht täglichen Umgang pflegt, ist erfahrungsgemäß von dieser Argumentation noch nicht überzeugt. In seinem Büchlein „Das Ziegenproblem – Denken in Wahrscheinlichkeiten“ sah sich Gero von Randow, seines Zeichens Journalist und Mitarbeiter DER ZEIT, gar veranlasst, die Beweisführung schier endlos zu variieren. Um die oben dargelegte ebenso kurze wie prägnante Begründung machte er indessen einen weiten Bogen. Vielleicht erschien sie im zu einfach, um wahr zu sein. Zu seiner Ehrenrettung muss man derweil anerkennen, dass sich zu Beginn der neunziger Jahre des letzten Jahrhunderts in der Denksportszene tatsächlich ein teilweise unsachlicher Disput zu dem seither so genannten „Ziegenproblem“ entzündet hatte, der rationaler Beilegung dringend bedurfte.
In diesem Sinne wollen wir daher eine einfachere Argumentationskette aufbauen und dabei möglichst wenig Wissen über Wahrscheinlichkeitsrechnung voraussetzen. Vielfach haben Menschen auch Schwierigkeiten, Symmetrien zu erkennen und Fälle zu verallgemeinern. Daher betrachten wir die Auswahlsituation im Folgenden weitgehend ohne symbolische Bezeichnungen und ohne vorschnelle Symmetrieüberlegungen. Zunächst benötigen wir eine Möglichkeit, die Problemstellung in der Spielshow überhaupt zu beschreiben. Dazu notieren wir einfach AZZ, wenn sich das Auto hinter der linken Tür befindet (und die Ziegen hinter der mittleren und der rechten Tür), ZAZ, wenn das Auto hinter der mittleren Tür steht, sowie ZZA, wenn der Gewinn hinter der rechten Tür ist.
Insgesamt haben wir also die folgenden drei Fälle:
- AZZ
- ZAZ
- ZZA
Mehr Möglichkeiten gibt es zunächst nicht. Nun müssen wir die Erstauswahl des Kandidaten kennzeichnen. Dazu können wir einfach den an der betreffenden Stelle stehenden Buchstaben unterstreichen. Z. B. meint dann die Zeichenfolge ZAZ, dass der Kandidat die linke Tür gewählt hat. Offenbar eine Ziege (von diesem Pech weiß er zu diesem Zeitpunkt aber noch nichts). Die möglichen neun Fälle bis zur Erstauswahl des Kandidaten sind in Tabelle 3‑1 aufgelistet.
| 1 | AZZ |
| 2 | ZAZ |
| 3 | ZZA |
| 4 | AZZ |
| 5 | ZAZ |
| 6 | ZZA |
| 7 | AZZ |
| 8 | ZAZ |
| 9 | ZZA |
Tabelle 3‑1
Alle neun Fälle sind gleichwahrscheinlich. Mit der Wahrscheinlichkeit ![]() wird also genau einer der aufgelisteten neun Verläufe realisiert.
wird also genau einer der aufgelisteten neun Verläufe realisiert.
Die daraufhin vom Moderator geöffnete Tür notieren wir durch einen kleinen Buchstaben an der nämlichen Stelle. Also etwa ZAz, wenn der Moderator die rechte Tür öffnet. Nun sind wir in der Lage, uns einen kompletten Überblick über alle denkbaren Fälle zu verschaffen. Man macht sich leicht klar, dass es bis hierher überhaupt nur die folgenden Ablaufmöglichkeiten in der Spielshow gibt (s. Tabelle 3‑2).
| 1 | AzZ | 1.1 | AzZ | ||
| AZz | 1.2 | AZz | |||
| 2 | ZAz | 2 | ZAz | ||
| 3 | ZzA | 3 | ZzA | ||
| 4 | AZz | 4 | AZz | ||
| 5 | zAZ | 5.1 | zAZ | ||
| ZAz | 5.2 | ZAz | |||
| 6 | zZA | 6 | zZA | ||
| 7 | AzZ | 7 | AzZ | ||
| 8 | zAZ | 8 | zAZ | ||
| 9 | zZA | 9.1 | zZA | ||
| ZzA | 9.2 | ZzA |
Tabelle 3‑2
Wenn die in den Zeilen 1, 5 und 9 notierten Fälle auftreten, hat der Moderator offensichtlich zwei Möglichkeiten zum Öffnen einer Ziegentür, weil in diesen Situationen der Kandidat mit seiner Erstauswahl zufälligerweise auf die Tür mit dem Hauptgewinn getippt hatte. Ändert dies etwas an der Wahrscheinlichkeit für das Eintreten der drei zugrunde liegenden Ereignisse AZZ, ZAZ oder ZZA? Natürlich nicht! Nach wie vor treten diese Situationen genau wie die anderen Ereignisse mit der Chance ![]() ein. Durch den Freiheitsgrad des Moderators spalten sich die genannten drei Fälle vielmehr in zwei untereinander gleichwahrscheinliche Fälle auf. Das heißt, die Spielshow nimmt bis zur Frage des Moderators: „Bleiben Sie bei Ihrer Wahl oder möchten Sie doch lieber zur anderen Tür wechseln?“ mit der Wahrscheinlichkeit von jeweils
ein. Durch den Freiheitsgrad des Moderators spalten sich die genannten drei Fälle vielmehr in zwei untereinander gleichwahrscheinliche Fälle auf. Das heißt, die Spielshow nimmt bis zur Frage des Moderators: „Bleiben Sie bei Ihrer Wahl oder möchten Sie doch lieber zur anderen Tür wechseln?“ mit der Wahrscheinlichkeit von jeweils ![]() genau einen der aufgelisteten sechs Verläufe nach den Zeilen 2, 3, 4, 6, 7, 8 der Tabelle und mit der Wahrscheinlichkeit von jeweils
genau einen der aufgelisteten sechs Verläufe nach den Zeilen 2, 3, 4, 6, 7, 8 der Tabelle und mit der Wahrscheinlichkeit von jeweils ![]() einen der sechs Verläufe nach den Zeilen 1.1, 1.2, 5.1, 5.2, 9.1, 9.2.
einen der sechs Verläufe nach den Zeilen 1.1, 1.2, 5.1, 5.2, 9.1, 9.2.
Was passiert nun, wenn der Kandidat bei seiner ersten Türauswahl bleibt? Er hat doch nur dann die richtige Wahl getroffen, wenn die den Zeilen 1.1, 1.2, 5.1, 5.2, 9.1, 9.2 entsprechenden Fälle vorliegen. Seine Gewinnchance ist daher ![]() (s. Tabelle 3‑3). Machen wir die Gegenprobe. Was geschieht, wenn der Kandidat die Tür wechselt? Tabelle 3‑3 entnimmt man ferner, dass dies für ihn von Vorteil ist, wenn die Situationen gemäß den Zeilen 2, 3, 4, 6, 7, 8 auftreten. Nachdem diesen Fällen jeweils die Realisierungschance
(s. Tabelle 3‑3). Machen wir die Gegenprobe. Was geschieht, wenn der Kandidat die Tür wechselt? Tabelle 3‑3 entnimmt man ferner, dass dies für ihn von Vorteil ist, wenn die Situationen gemäß den Zeilen 2, 3, 4, 6, 7, 8 auftreten. Nachdem diesen Fällen jeweils die Realisierungschance ![]() zukommt, ist seine Gewinnwahrscheinlichkeit bei der Wechselstrategie
zukommt, ist seine Gewinnwahrscheinlichkeit bei der Wechselstrategie ![]() .
.
| 1.1 | AzZ | Der Kandidat gewinnt, wenn er bei seiner Auswahl bleibt. | |
| 1.2 | AZz | Der Kandidat gewinnt, wenn er bei seiner Auswahl bleibt. | |
| 2 | ZAz | Der Kandidat gewinnt, wenn er wechselt. | |
| 3 | ZzA | Der Kandidat gewinnt, wenn er wechselt. | |
| 4 | AZz | Der Kandidat gewinnt, wenn er wechselt. | |
| 5.1 | zAZ | Der Kandidat gewinnt, wenn er bei seiner Auswahl bleibt. | |
| 5.2 | ZAz | Der Kandidat gewinnt, wenn er bei seiner Auswahl bleibt. | |
| 6 | zZA | Der Kandidat gewinnt, wenn er wechselt. | |
| 7 | AzZ | Der Kandidat gewinnt, wenn er wechselt. | |
| 8 | zAZ | Der Kandidat gewinnt, wenn er wechselt. | |
| 9.1 | zZA | Der Kandidat gewinnt, wenn er bei seiner Auswahl bleibt. | |
| 9.2 | ZzA | Der Kandidat gewinnt, wenn er bei seiner Auswahl bleibt. |
Tabelle 3‑3
Damit sind wir mit der denkbar breitesten Beweisführung am Ende. Entscheidend ist Folgendes: nach der Auswahl des Kandidaten öffnet der Moderator mit Sicherheit eine Ziegentür. Er sortiert also eine Niete aus und gibt damit unausgesprochen einen Hinweis auf die Tür, hinter der in zwei von drei Fällen der Hauptgewinn steht: eben die andere, vom Kandidaten ursprünglich nicht gewählte Tür. Viel mehr Zweckdienliches kann man dazu nun wirklich nicht mehr beitragen. Gelegentlich trifft man dennoch auf wunderliche Einwände oder Missverständnisse. Z. B. auf dieses: wenn der Moderator zufällig irgendeine Tür öffnet, dann ist die die Wechselstrategie ebenfalls günstiger. Das ist natürlich Unsinn. Die Wechselstrategie ist doch gerade deswegen von Vorteil, weil der Moderator nicht irgendeine Tür öffnet, sondern garantiert eine Ziegentür aussondert. Die Gewinnchance des Kandidaten ist bei zufälliger Türauswahl durch den Moderator nur ![]() , und zwar unabhängig davon, ob der Kandidat nun bei seiner ersten Türauswahl bleibt oder ob er wechselt, denn in einem Drittel aller Fälle öffnet der Moderator zwangsläufig die Tür mit dem Auto. Für den Kandidaten gibt es daher nur noch in zwei von drei Fällen überhaupt etwas zu gewinnen. Der Gewinn befindet sich nur mit
, und zwar unabhängig davon, ob der Kandidat nun bei seiner ersten Türauswahl bleibt oder ob er wechselt, denn in einem Drittel aller Fälle öffnet der Moderator zwangsläufig die Tür mit dem Auto. Für den Kandidaten gibt es daher nur noch in zwei von drei Fällen überhaupt etwas zu gewinnen. Der Gewinn befindet sich nur mit ![]() Wahrscheinlichkeit hinter den beiden verschlossenen Türen. Die nicht gewählte Tür verbirgt das Auto folglich nur mit der Chance
Wahrscheinlichkeit hinter den beiden verschlossenen Türen. Die nicht gewählte Tür verbirgt das Auto folglich nur mit der Chance ![]() .
.
3.2 Das Ziegenproblem mit mehr als 3 Türen
Im vorstehenden Abschnitt sollte eigentlich alles klar geworden sein. Wenn indessen die Erläuterungen nach einer gewissen Zeit in Vergessenheit geraten sind, mögen wieder Zweifel aufkommen: Ist das wirklich so simpel? Bringt das Wechseln wirklich was? Um diese Zweifel ein für allemal auszuräumen, wollen wir im Folgenden die sozusagen ultimative Klarheit herstellen. Dazu erweitern wir das Spiel in sinngemäßer Weise um weitere 7 Türen, so dass wir nun die folgende Spielsituation vorfinden:
- Ein Kandidat steht vor 10 verschlossenen Türen. Hinter einer Tür befindet sich der vom Kandidaten erstrebte Gewinn, ein Auto, hinter den 9 anderen Türen je eine Ziege. Der Moderator bittet den Kandidaten, eine Tür zu auswählen, was dieser in Erwartung des Preises gerne tut. Die gewählte Tür bleibt aber vorerst geschlossen. Nun zeigt der Moderator, der weiß, hinter welcher Tür sich das Auto befindet, mit den Worten „Ich zeig` Ihnen `mal `was“ auf eine andere Tür und öffnet sie. Dahinter steht eine Ziege. Es gibt nun nur noch 9 verschlossene Türen, die vom Kandidaten gewählte und 8 andere. Dem Kandidaten wird nunmehr die Frage gestellt: „Bleiben Sie bei Ihrer Wahl oder möchten Sie doch lieber zu einer anderen Tür wechseln?“
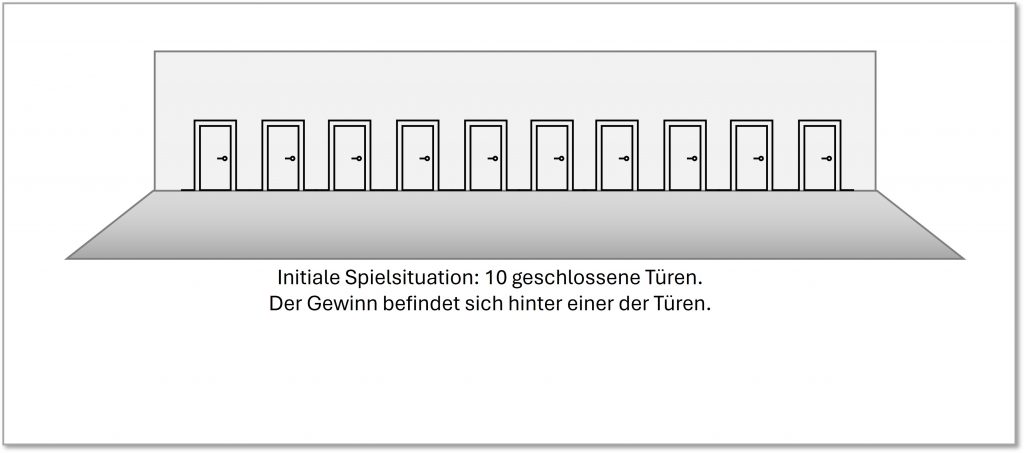
Abbildung 3-1
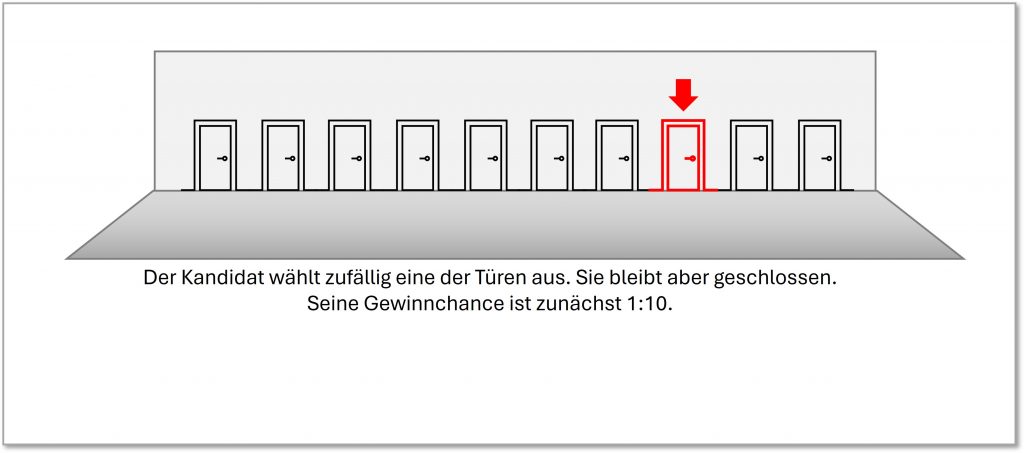
Abbildung 3-2
Na ja, wird man sich jetzt fragen: Worin liegt hier denn die Vereinfachung? Eigentlich ist man jetzt doch nicht klüger als im Originalspiel. Und ob das Wechseln zu einer anderen Tür etwas bringt, ist unklarer als zuvor.
Einen Moment noch, es wird gleich deutlich werden.
Zunächst einmal macht man sich klar, dass der Gewinn unzweifelhaft mit der Wahrscheinlichkeit ![]() hinter der vom Kandidaten gewählten Tür steht. Die anderen 9 anfänglich alle verschlossen gewesenen Türen verbergen den Gewinn, also das Auto, folglich mit der Wahrscheinlichkeit
hinter der vom Kandidaten gewählten Tür steht. Die anderen 9 anfänglich alle verschlossen gewesenen Türen verbergen den Gewinn, also das Auto, folglich mit der Wahrscheinlichkeit ![]() . Sobald nun der Moderator eine Tür öffnet – und er wird dazu, wie im Originalspiel, mit absoluter Sicherheit eine Ziegentür wählen – haben wir über die vom Kandidaten gewählte Tür hinaus nur noch 8 verschlossene Türen. Hinter diesen 8 Türen befindet sich der Gewinn nach wie vor mit
. Sobald nun der Moderator eine Tür öffnet – und er wird dazu, wie im Originalspiel, mit absoluter Sicherheit eine Ziegentür wählen – haben wir über die vom Kandidaten gewählte Tür hinaus nur noch 8 verschlossene Türen. Hinter diesen 8 Türen befindet sich der Gewinn nach wie vor mit ![]() -Wahrscheinlichkeit. Daran hat sich ja nichts geändert. Die Chance, das Auto hinter einer dieser 8 Türen zu finden ist daher
-Wahrscheinlichkeit. Daran hat sich ja nichts geändert. Die Chance, das Auto hinter einer dieser 8 Türen zu finden ist daher
(1) 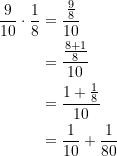
Die Gewinnwahrscheinlichkeit beim Wechseln auf eine dieser 8 verschlossenen Türen ist demnach um den Wert ![]() größer als im Falle der vom Kandidaten zunächst gewählten Tür. Das ist nicht viel, aber es zeigt, dass der Wechsel von Vorteil ist.
größer als im Falle der vom Kandidaten zunächst gewählten Tür. Das ist nicht viel, aber es zeigt, dass der Wechsel von Vorteil ist.
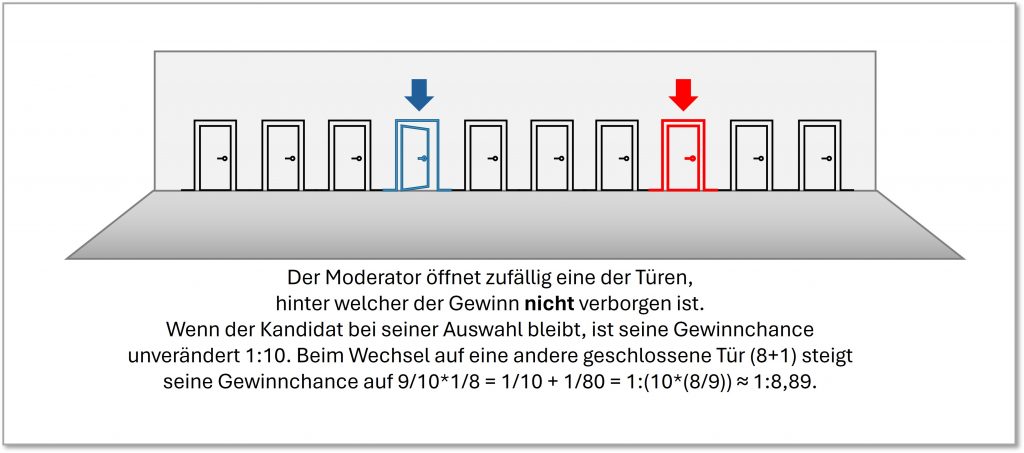
Abbildung 3-3
Immer noch nicht überzeugt? Kein Wunder, der Vorteil ist einfach noch zu gering und daher kaum sichtbar. Er wird aber gleich sehr viel größer werden. Wir setzen das Spiel nämlich fort.
- Der Moderator, der natürlich immer noch weiß, hinter welcher Tür sich das Auto befindet, öffnet mit den Worten „Ich zeig` Ihnen nochmal `was“ auf eine weitere Tür. Dahinter steht wieder eine Ziege. Es gibt nun nur noch 8 verschlossene Türen, die vom Kandidaten gewählte und 7 weitere. Dem Kandidaten wird nunmehr erneut die Frage gestellt: „Bleiben Sie bei Ihrer Wahl oder möchten Sie doch lieber zu einer anderen Tür wechseln?“
Wie stellt sich die Entscheidungssituation nun dar?
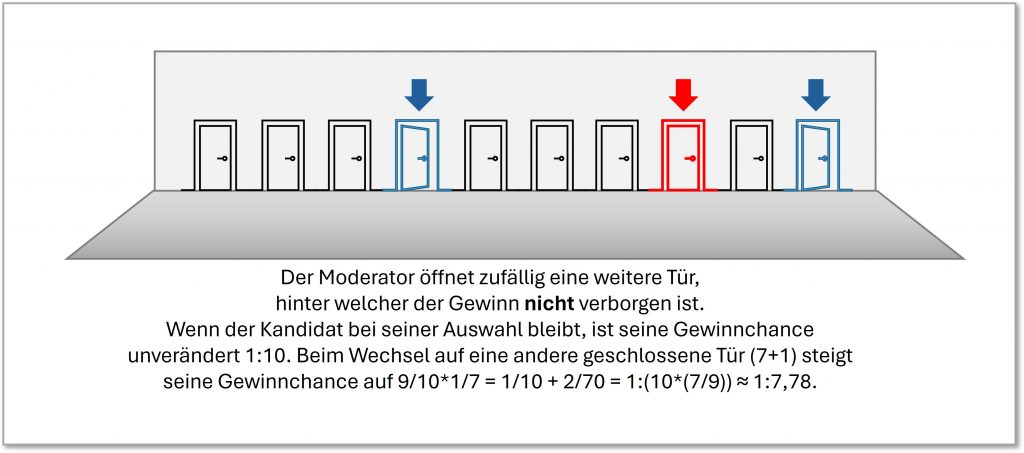
Abbildung 3-4
Immer noch steht das Auto mit der Wahrscheinlichkeit ![]() hinter der vom Kandidaten gewählten Tür steht. Die anderen 7 noch verschlossenen Türen verbergen den Gewinn folglich nach wie vor mit der Wahrscheinlichkeit
hinter der vom Kandidaten gewählten Tür steht. Die anderen 7 noch verschlossenen Türen verbergen den Gewinn folglich nach wie vor mit der Wahrscheinlichkeit ![]() . Daran hat sich nichts geändert. Die Chance, das Auto hinter einer dieser 7 Türen zu finden ist daher
. Daran hat sich nichts geändert. Die Chance, das Auto hinter einer dieser 7 Türen zu finden ist daher
(2) 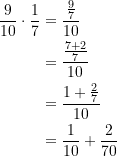
Die Gewinnwahrscheinlichkeit beim Wechseln auf eine dieser 7 verschlossenen Türen ist demnach um den Wert ![]() größer als im Falle der vom Kandidaten zunächst gewählten Tür. Der Wechsel zu einer dieser Türen ist also von Vorteil. Es wird gleich noch viel besser.
größer als im Falle der vom Kandidaten zunächst gewählten Tür. Der Wechsel zu einer dieser Türen ist also von Vorteil. Es wird gleich noch viel besser.
Nun setzen wir das Spiel sinngemäß fort:
- Der Moderator öffnet Schritt für Schritt eine Tür nach der anderen – natürlich nicht die Tür mit dem Auto, sofern sie überhaupt unter den vom Kandidaten nicht gewählten Türen zu finden ist – und stellt dem Kandidaten immer wieder erneut die Frage: „Bleiben Sie bei Ihrer Wahl oder möchten Sie doch lieber zu einer anderen Tür wechseln? – Ach was, warten Sie, ich öffne noch eine weitere Tür“.
In diesem Prozess sind dann also erst 8 (s. Abb. 3-4), dann 7 (s. Abb. 3-5), dann 6, 5, 4, 3 (s. Abb. 3-6), und zuletzt nur noch 2 Türen (s. Abb. 3-7) verschlossen, nämlich die vom Kandidaten gewählte und die vom Moderator final noch nicht geöffnete Tür. Der Kandidat hat dann letztlich die Wahl, ob er bei seiner zuerst gewählten Tür bleibt oder zur anderen noch verschlossenen Tür wechselt. Was soll er tun?
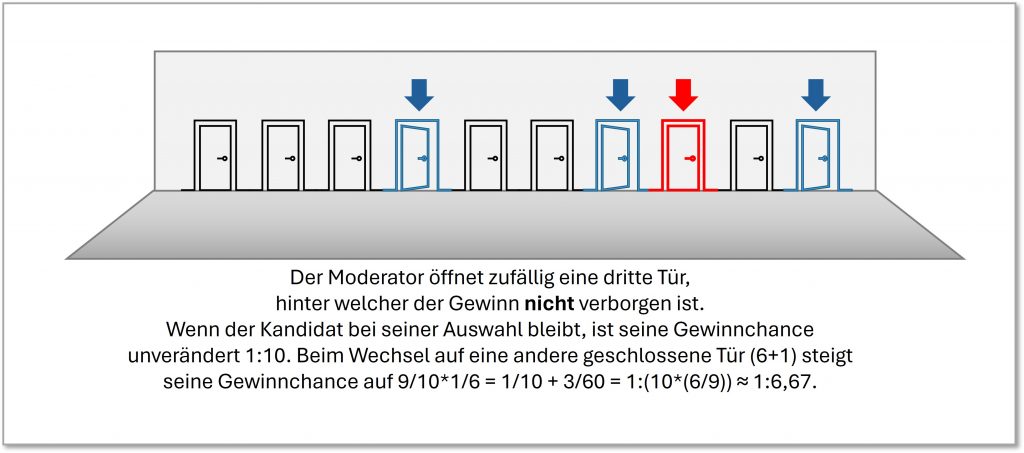
Abbildung 3-5
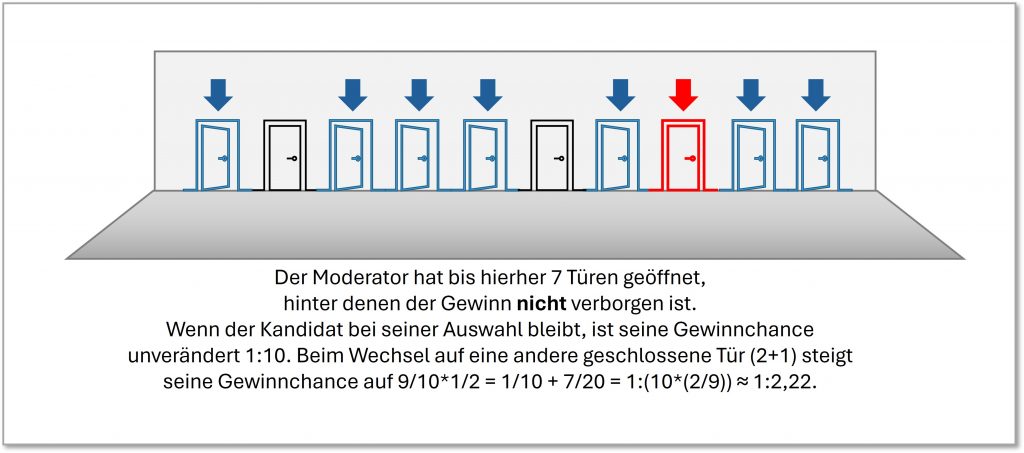
Abbildung 3-6
Das ist seine finale Entscheidungssituation:
- Der Gewinn befindet sich mit der Wahrscheinlichkeit
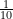 hinter der vom Kandidaten gewählten Tür.
hinter der vom Kandidaten gewählten Tür. - Die andere, noch verschlossene Tür verbirgt den Gewinn mit der Wahrscheinlichkeit
(3) 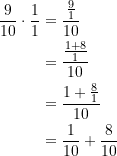
Anmerkung: Der eigentlich triviale Rechengang wird hier nur deswegen im Detail ausgebreitet, um die Analogie zur vorhergehenden Situation mit mehr als 2 geschlossenen Türen aufzuzeigen.
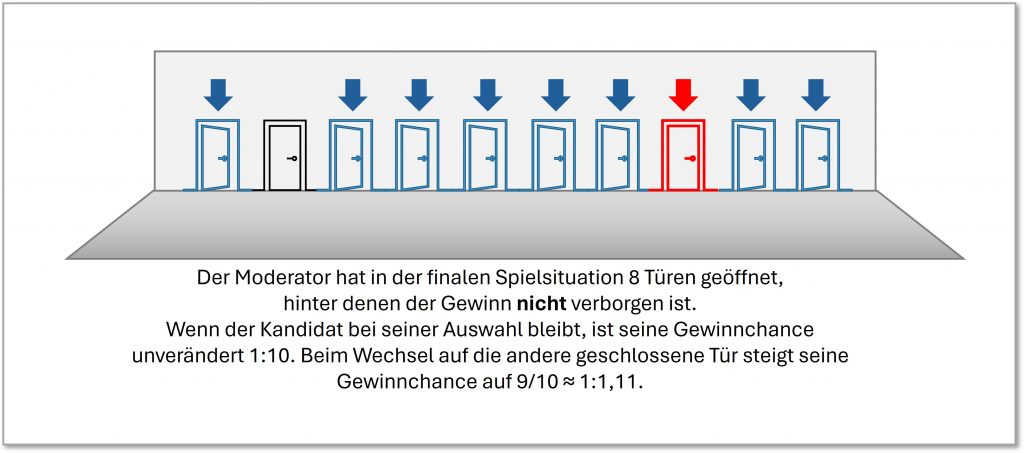
Abbildung 3-7
Damit ist klar, dass der Wechsel auf jeden Fall eine erhebliche Steigerung der Gewinnchance verspricht: Der Kandidat kann durch den Wechsel seine Gewinnchance von ![]() auf
auf ![]() erhöhen.
erhöhen.
Wir haben im Falle der 10 Türen im Prinzip die gleiche Entscheidungssituation, wie im ursprünglichen Spiel mit 3 Türen. Allerdings ist jetzt der Unterschied in der Gewinnwahrscheinlichkeit beim Wechseln sehr viel größer: Bei 3 Türen verdoppelt sich die Gewinnchance, bei 10 Türen haben wir eine Verneunfachung der Gewinnwahrscheinlichkeit.
Wenn man den Ablauf des Spiels Revue passieren lässt, dann sollte die Argumentation für den Wechsel unmittelbar einleuchten: Der Moderator sortiert beim Öffnen einer weiteren Tür jedesmal eine Niete aus. Wie im Originalspiel ist genau das der entscheidende Punkt. Da in 9 von 10 Fällen der Gewinn nicht hinter der vom Kandidaten ursprünglich gewählten Tür verborgen ist, muss das Auto zwangsläufig mit eben dieser Wahrscheinlichkeit von ![]() hinter der anderen, also der vom Moderator bis zuletzt nicht geöffneten Tür stehen.
hinter der anderen, also der vom Moderator bis zuletzt nicht geöffneten Tür stehen.
Und wie stellt sich die Entscheidungssituation dar, wenn nun ein zweiter Kandidat hinzustößt, der nichts von alledem mitbekommen hat und nur die beiden verbliebenen geschlossenen Türen sieht? Hinter einer Tür befindet sich der Gewinn, hinter der anderen steht eine Ziege. Wie soll er sich entscheiden? Ist seine Gewinnchance nicht einfach 50 %? – Es wird wirklich ein wenig paradox: Wenn er vor den beiden Türen steht und sonst keine Informationen hat, dann ist seine Gewinnchance tatsächlich 1:2. Der erste Kandidat kann den Gewinn dagegen mit der Chance 9:10 abräumen (sofern er wechselt). Liegt darin nicht ein Widerspruch? – Keineswegs!
Dem zweiten Kandidaten fehlen jegliche Informationen darüber, hinter welcher Tür sich der Gewinn verbirgt. Seine bestmögliche Ausgangsposition ist daher die Annahme einer Gleichverteilung der Gewinnchance über die beiden Türen. Er hat keine Grundlage für das Präferieren einer der beiden Türen. Folglich wird er mit 50-prozentiger Wahrscheinlichkeit die Tür nehmen, hinter welcher der Gewinn in 9 von 10 Fällen steht (wovon er aber nichts weiß). Ebenfalls mit einer Wahrscheinlichkeit von 50 % wird er die andere Tür wählen, also die Tür hinter der der Gewinn nur in 1 von 10 Fällen steht. Seine finale Gewinnchance ist daher
(4) ![]()
Das gleiche gilt natürlich auch für den ersten Kandidaten, sofern er den Spielverlauf ignoriert und sich auf den Standpunkt stellt, es sei egal, wofür er sich entscheidet. Nehmen wir an, er werfe eine Münze. Wenn Zahl fällt, bleibt er bei seiner Tür, fällt Kopf, wechselt er zur anderen Tür. Im Ergebnis ist seine Gewinnwahrscheinlichkeit ebenso 50 %, wie die des zweiten – unwissenden – Kandidaten.
Der zweite Kandidat verhält sich daher absolut vernünftig im Rahmen seines Kenntnisstands auf Basis der rationalen Annahme eines gleichverteilten Gewinns. Ein besseres Ergebnis kann er im Allgemeinen nicht erzielen. Wenn man ihn indessen über die anfängliche Spielsituation und den Verlauf des Spiels aufklärt, dann wird er seine zunächst nicht unvernünftige Annahme einer Geichverteilung der Gewinnchance über die beiden Türen revidieren. Er kommt derart – genau wie der erste Kandidat – zur Gewinnchancenverteilung ![]() zu
zu ![]() und wird natürlich die Tür wählen, die der Moderator bis zuletzt nicht geöffnet hatte, womit er seine Gewinnchance auf
und wird natürlich die Tür wählen, die der Moderator bis zuletzt nicht geöffnet hatte, womit er seine Gewinnchance auf ![]() steigert.
steigert.
Wenn im allgemeinen Fall die theoretische Gewinnwahrscheinlichkeit ![]() ist, der Kandidat aber die entsprechende Tür nur mit der Wahrscheinlichkeit
ist, der Kandidat aber die entsprechende Tür nur mit der Wahrscheinlichkeit ![]() öffnet, dann realisiert er damit den Gewinn tatsächlich mit der Wahrscheinlichkeit
öffnet, dann realisiert er damit den Gewinn tatsächlich mit der Wahrscheinlichkeit
(5) 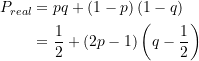
In der ersten Zeile der Formel erkennt man, dass die realisierte Gewinnwahrscheinlichkeit ![]() ist, wenn
ist, wenn ![]() , wenn also der Kandidat mit Sicherheit die spielstrategisch empfohlene Tür öffnet (für die natürlich
, wenn also der Kandidat mit Sicherheit die spielstrategisch empfohlene Tür öffnet (für die natürlich ![]() gilt). Entscheidet er sich für die andere Tür, d.h.
gilt). Entscheidet er sich für die andere Tür, d.h. ![]() , dann ist
, dann ist ![]() . Alle Werte dazwischen sind ebenfalls möglich, sofern der Kandidat eine gemischte Strategie verfolgt und sich mal so, mal so entscheidet. Wenn er eine Münze wirft, womit
. Alle Werte dazwischen sind ebenfalls möglich, sofern der Kandidat eine gemischte Strategie verfolgt und sich mal so, mal so entscheidet. Wenn er eine Münze wirft, womit ![]() zu setzen ist, ergibt sich stets die Gewinnwahrscheinlichkeit
zu setzen ist, ergibt sich stets die Gewinnwahrscheinlichkeit ![]() . Dies kann man unmittelbar der zweiten Zeile der Formel entnehmen.
. Dies kann man unmittelbar der zweiten Zeile der Formel entnehmen.
Daraus ergibt sich folgende, etwas paradoxe Situation: Kandidaten, die in völliger Ignoranz des Spielverlaufs darauf beharren, es sei egal, welche Tür sie letztlich öffneten, weil der Gewinn – ihrer Meinung nach – mit gleicher Wahrscheinlichkeit hinter der einen wie hinter der anderen Tür stehen könnte, werden durch das Ergebnis bestätigt, weil sich ja tatsächlich die realisierte Gewinnwahrscheinlichkeit ![]() einstellt. Und dies ganz unabhängig von der theoretischen Gewinnwahrscheinlichkeit
einstellt. Und dies ganz unabhängig von der theoretischen Gewinnwahrscheinlichkeit ![]() . Natürlich ist das kein Paradoxon, sondern sehr einfach erklärbar (s. obige Formel (5)). Immerhin ist diese Fifty-Fifty-Strategie des Kandidaten im Allgemeinen immer noch besser, als stur auf der Orignialtür zu beharren und dann den Gewinn nur mit
. Natürlich ist das kein Paradoxon, sondern sehr einfach erklärbar (s. obige Formel (5)). Immerhin ist diese Fifty-Fifty-Strategie des Kandidaten im Allgemeinen immer noch besser, als stur auf der Orignialtür zu beharren und dann den Gewinn nur mit ![]() zu realisieren.
zu realisieren.
Zum Grundsätzlichen beim Spiel mit ![]() Türen:
Türen:
Wenn ![]() von
von ![]() Türen geöffnet sind, stellt sich die Entscheidungssituation wie folgt dar:
Türen geöffnet sind, stellt sich die Entscheidungssituation wie folgt dar:
- Hinter der vom Kandidaten gewählten Tür steht das Auto mit der Wahrscheinlichkeit
 .
.
- Jede einzele unter den anderen noch nicht geöffneten Türen verbirgt den Gewinn mit der Wahrscheinlichkeit
(6) 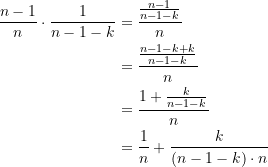
Sobald alle bis auf die letzten 2 Türen geöffnet sind, wenn also ![]() gilt, dann ist somit die Gewinnchance beim Wechseln:
gilt, dann ist somit die Gewinnchance beim Wechseln:
(7) 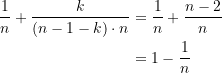
Wir können ![]() beliebig erhöhen,
beliebig erhöhen, ![]() . Wer mag im Falle von
. Wer mag im Falle von ![]() Türen in der finalen Situation, wenn nur noch 2 Türen geschlossen sind, in der Haltung verharren, es sei egal, ob man wechselt, oder nicht?
Türen in der finalen Situation, wenn nur noch 2 Türen geschlossen sind, in der Haltung verharren, es sei egal, ob man wechselt, oder nicht?
Bei Spielvarianten mit größerem ![]() strebt die Gewinnchance beim Wechseln gegen 1. Kandidaten, die bei ihrer ursprünglich gewählten Tür bleiben, müssen sich mit der Gewinnwahrscheinlichkeit 1 zu n bescheiden. Ihre Gewinnchance strebt daher gegen 0.
strebt die Gewinnchance beim Wechseln gegen 1. Kandidaten, die bei ihrer ursprünglich gewählten Tür bleiben, müssen sich mit der Gewinnwahrscheinlichkeit 1 zu n bescheiden. Ihre Gewinnchance strebt daher gegen 0.
Noch einmal kurz zurück zur Orginalvariante mit 3 Türen. In diesem Falle gilt ![]() und
und ![]() . In die obige Formel eingesetzt, erhalten wir die Gewinnchance beim Wechseln in Übereinstimmung mit der Ableitung in Abschnitt 3.1 zu
. In die obige Formel eingesetzt, erhalten wir die Gewinnchance beim Wechseln in Übereinstimmung mit der Ableitung in Abschnitt 3.1 zu
(8) 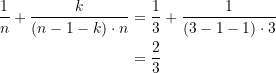
Übrigens, statt der Türen kann man auch ![]() Lose mit genau einem Gewinn und folglich
Lose mit genau einem Gewinn und folglich ![]() Nieten nehmen. Der Kandidat zieht ein Los. Der Moderator öffnet dann analog nach und nach ein Los nach dem anderen – natürlich nur Nieten, wie im Originalspiel – und frägt den Spieler zuletzt, also dann, wenn insgesamt nur noch 2 Lose übrig sind, ob er sein anfänglich gezogenes Los mit dem übrig gebliebenen anderen Los tauschen möchte. Tut er’s, erhöht sich seine Gewinnchance auf
Nieten nehmen. Der Kandidat zieht ein Los. Der Moderator öffnet dann analog nach und nach ein Los nach dem anderen – natürlich nur Nieten, wie im Originalspiel – und frägt den Spieler zuletzt, also dann, wenn insgesamt nur noch 2 Lose übrig sind, ob er sein anfänglich gezogenes Los mit dem übrig gebliebenen anderen Los tauschen möchte. Tut er’s, erhöht sich seine Gewinnchance auf ![]() , ansonsten bleibt seine Gewinnwahrscheinlichkeit bei
, ansonsten bleibt seine Gewinnwahrscheinlichkeit bei ![]() .
.
3.3 Das Ziegenproblem mit mehreren Moderatoren
Eine Zweidrittel-Gewinnchance beim Wechseln der Tür wie im Originalspiel ist nicht schlecht. Kann man diese Chance noch verbessern? Im Allgemeinen nein. Was sieht es aber aus, wenn der Sender zwei Moderatoren mit der Durchführung des Spiels beauftragt? Nehmen wir an, das Spiel läuft zunächst wie beschrieben.
- Ein Moderator leitet das Spiel, der zweite befindet sich noch in der Maske, also hinter den Kulissen. Beide Moderatoren wissen, wo der Hauptgewinn verborgen ist. Der Kandidat wählt also eine Tür. Der erste Moderator zeigt auf eine vom Kandidaten nicht gewählte Tür, öffnet sie aber nicht und bemerkt nur: „Hinter dieser Tür steht eine Ziege, das kann ich Ihnen schon ´mal sagen“. Daraufhin kommt der zweite Moderator – der dies nicht mitbekommen hat – auf die Bühne und fragt den Kandidaten: „Na, welche Tür haben Sie denn gewählt?“ Im beglückenden Gefühl, seinem Gewinn ganz nahe zu sein, da ja nun schon eine Ziegentür benannt wurde, deutet der Kandidat erneut auf seine gewählte Tür. Mit den Worten „Dann will ich Ihnen `mal `was zeigen“ weist sodann der zweite Moderator auf eine vom Kandidaten nicht gewählte Tür und öffnet sie. Dahinter steht eine Ziege. Danach stellt der erste Moderator wieder die entscheidende Frage: „Bleiben Sie bei Ihrer Wahl oder möchten Sie doch lieber zur anderen Tür wechseln?“
Die Entscheidungssituation des Kandidaten ist ähnlich wie oben: es gibt zwei verschlossene Türen, hinter einer Tür steht eine Ziege, hinter der anderen ein Auto. Es gibt aber einen wesentlichen Unterschied: die vom ersten Moderator benannte Tür muss nicht zwangsläufig die sein, die der zweite Moderator tatsächlich öffnet. Ist es dennoch die gleiche Tür, so wird der Kandidat durch die Anwesenheit des zweiten Moderators nicht klüger. Der Kandidat befindet sich in der gleichen Situation wie im Ein-Moderator-Spiel. Er kann daher durch Wechseln seine Gewinnchance verdoppeln. Wenn nun aber die beiden Moderatoren auf unterschiedliche Türen zeigen, so weiß der Kandidat bereits mit Sicherheit, wo der Hauptgewinn ist, denn das kann ja offensichtlich nur dann vorkommen, wenn sich das Auto hinter der vom Kandidaten gewählten Tür befindet. Der Kandidat muss demnach eine gemischte Strategie fahren:
- Auswahl wechseln, wenn beide Moderatoren auf dieselbe Tür zeigen.
- Trivialerweise bei seiner Wahl bleiben, wenn die Moderatoren auf verschiedene Türen zeigen.
Wie groß ist nun seine Gewinnwahrscheinlichkeit? In ![]() aller Fälle gewinnt er mit der Wechselstrategie (s. Zeilen 2, 3, 4, 6, 7, 8 nach Tabelle 3‑3). In dem verbleibenden Drittel der Möglichkeiten (s. Zeilen 1.1, 1.2, 5.1, 5.2, 9.1, 9.2 nach Tabelle 3‑3). deuten die beiden Moderatoren mit 50%-iger Wahrscheinlichkeit auf zwei verschiedene Türen. Dann weiß der Kandidat mit Sicherheit, dass er bereits die Tür mit dem Auto gewählt hat. Zeigen sie allerdings auf die gleiche Tür, so verspielt er durch Wechseln seinen Gewinn. Die Gewinnwahrscheinlichkeit beim Spiel mit zwei Moderatoren ist daher
aller Fälle gewinnt er mit der Wechselstrategie (s. Zeilen 2, 3, 4, 6, 7, 8 nach Tabelle 3‑3). In dem verbleibenden Drittel der Möglichkeiten (s. Zeilen 1.1, 1.2, 5.1, 5.2, 9.1, 9.2 nach Tabelle 3‑3). deuten die beiden Moderatoren mit 50%-iger Wahrscheinlichkeit auf zwei verschiedene Türen. Dann weiß der Kandidat mit Sicherheit, dass er bereits die Tür mit dem Auto gewählt hat. Zeigen sie allerdings auf die gleiche Tür, so verspielt er durch Wechseln seinen Gewinn. Die Gewinnwahrscheinlichkeit beim Spiel mit zwei Moderatoren ist daher
(9) 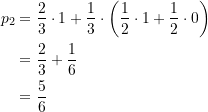
Nun kann man den Gedanken natürlich fortspinnen und 3, 4, 5 usw. Moderatoren bemühen. Oder etwa sinngemäß das Publikum einschalten. In all diesen Fällen erhöht sich die Gewinnerwartung bei Anwendung der angepassten Wechselstrategie:
- Auswahl wechseln, wenn alle Moderatoren auf dieselbe Tür zeigen.
- Trivialerweise bei seiner Wahl bleiben, wenn die Moderatoren auf verschiedene Türen zeigen.
Nun werden ![]() Moderatoren nur mit der Chance
Moderatoren nur mit der Chance ![]() unter zwei möglichen Ziegentüren stets auf die gleiche Tür zeigen. Mit der Wahrscheinlichkeit
unter zwei möglichen Ziegentüren stets auf die gleiche Tür zeigen. Mit der Wahrscheinlichkeit ![]() sind es daher verschiedene Türen. Allgemein erhält man dergestalt die Gewinnwahrscheinlichkeit beim Spiel mit
sind es daher verschiedene Türen. Allgemein erhält man dergestalt die Gewinnwahrscheinlichkeit beim Spiel mit ![]() Moderatoren
Moderatoren
(10) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} {p}_{m}&=\frac{2}{3}\cdot 1+\frac{1}{3}\cdot \left[ \left( 1-\frac{1}{2^{m-1}} \right)\cdot 1+\frac{1}{2^{m-1}}\cdot 0 \right]\\ &=1-\frac{2}{3}\cdot 2^{-m}\\ &=\frac{3\cdot 2^{m-1}-1}{3\cdot 2^{m-1}} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-cd02b9871e1f13e4cb576e3bfe759cb9_l3.png)
Für ![]() ist die Gewinnchance demnach
ist die Gewinnchance demnach ![]() , bei
, bei ![]() sogar
sogar ![]() .
.
Setzt man in die Formel ![]() ein, so erhält man natürlich wieder des Resultat
ein, so erhält man natürlich wieder des Resultat ![]() für das Originalspiel mit einem Moderator.
für das Originalspiel mit einem Moderator.
Übrigens, Kandidaten die nicht wechseln, müssen sich nach wie vor mit einer Gewinnchance von ![]() bescheiden, weil sie ja von der Zusatzinformation durch mehrere Moderatoren nicht profitieren.
bescheiden, weil sie ja von der Zusatzinformation durch mehrere Moderatoren nicht profitieren.


