Die nachfolgende Arbeit nimmt Bezug auf das von T. H. Gronwall definierte Verfahren zur Summierung von konvergenten und divergenten unendlichen Reihen auf Basis konformer Abbildungen. Das Summationsverfahren arbeitet mit geeigneten analytischen Funktionen ![]() und
und ![]() mit den folgenden Eigenschaften:
mit den folgenden Eigenschaften:
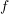 ist holomorph auf
ist holomorph auf 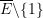 und stetig in
und stetig in 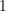
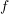 ist schlicht in
ist schlicht in 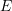 und
und 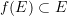
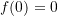 und
und 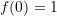
- Die Umkehrfunktion von
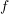 ist holomorph auf
ist holomorph auf 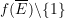
- Es gibt ein
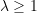 und eine um den Nullpunkt entwickeltbare Potenzreihe
und eine um den Nullpunkt entwickeltbare Potenzreihe 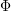 mit einem nicht verschwindendem Konvergenzradius, so dass
mit einem nicht verschwindendem Konvergenzradius, so dass 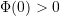 und
und 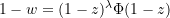 für
für 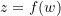 genügend nahe bei
genügend nahe bei 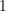
Hierbei ist ![]() .
.
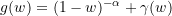 mit
mit 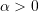 und
und 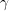 holomorph auf
holomorph auf 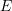 .
.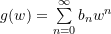 mit
mit 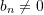 für alle
für alle 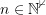
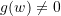 für alle
für alle 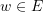
Nun wird der Reihe ![]() über die Identität
über die Identität
![]()
eine Folge ![]() zugeordnet.
zugeordnet.
Die Reihe ![]() heißt
heißt ![]() -summierbar zur Summe
-summierbar zur Summe ![]() , wenn
, wenn ![]() für
für ![]() .
.
Entsprechend nennen wir eine Folge ![]()
![]() -limitierbar zum Grenzwert
-limitierbar zum Grenzwert ![]() , wenn eine Identität
, wenn eine Identität
![]()
besteht und ![]() für
für ![]() .
.
Wenn wir ![]() , also
, also ![]() , und
, und ![]() setzen, also
setzen, also ![]() , so erhalten wir das Gronwall-Verfahren, das im Sinne der letzten Identität auf
, so erhalten wir das Gronwall-Verfahren, das im Sinne der letzten Identität auf
![]()
hinausläuft. Wie man leicht erkennt, ist in diesem Falle ![]() . M. a. W., das Gronwall-Verfahren
. M. a. W., das Gronwall-Verfahren ![]() ist konvergenzgleich, d.h., es summiert eine Reihe genbau dann, wenn diese Reihe konvergent ist.
ist konvergenzgleich, d.h., es summiert eine Reihe genbau dann, wenn diese Reihe konvergent ist.
Betrachten wir als weiteres Beispiel das Gronwall-Verfahren ![]() mit
mit ![]() (also
(also ![]() ) und
) und ![]() und wenden es auf die Reihe
und wenden es auf die Reihe
![]()
oder, was das selbe bedeutet, auf die Folge
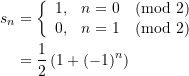
an. Natürlich ist diese Reihe im klassischen Sinne nicht konvergent, das sieht man ganz einfach daran, dass die Folge der Partialsummen zwei Häufungspunkte hat, genauer, dass sie unendlich oft die Werte ![]() und
und ![]() annimmt.
annimmt.
Nach dem Obigen haben wir jetzt
![]()
Wegen ![]() folgt daraus
folgt daraus
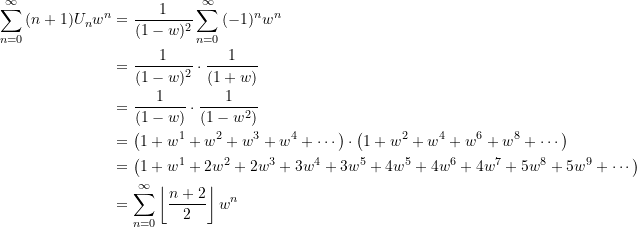
Durch Koeffizientenvergeich erhalten wir daraus
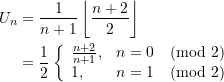
und damit
![]()
Im Ergebnis ist also die ![]() -Summe von
-Summe von ![]() für
für ![]() (also
(also ![]() ) und
) und ![]() gleich
gleich ![]() .
.
Formal:
![]()
Dieses Gronwall-Verfahren summiert also auch divergente Reihen.
Für Näheres siehe PDF-Dokument im nachfolgenden Link:


