Eine Frage vor der man gelegentlich steht: Lohnt sich der Umweg? Nehmen wir z.B. die Situation beim Tanken. Wir befinden uns an einer Position ![]() (Start) und wollen eigentlich auf kürzestem Wege nach
(Start) und wollen eigentlich auf kürzestem Wege nach ![]() (Ziel). Der Tank ist fast leer, wahrscheinlich reicht es aber noch bis ans Ziel. Entlang des Weges gibt es eine Tankstelle
(Ziel). Der Tank ist fast leer, wahrscheinlich reicht es aber noch bis ans Ziel. Entlang des Weges gibt es eine Tankstelle ![]() , dort kostet der Sprit pro Liter den Betrag
, dort kostet der Sprit pro Liter den Betrag ![]() . Natürlich gibt es auch andere, längere Wege zum Ziel. In Zeiten des mobilen Internets erfahren wir ganz leicht, dass es in der weiteren Umgebung eine zweite Tankstelle
. Natürlich gibt es auch andere, längere Wege zum Ziel. In Zeiten des mobilen Internets erfahren wir ganz leicht, dass es in der weiteren Umgebung eine zweite Tankstelle ![]() gibt, dort kostet der Sprit pro Liter den (geringeren) Betrag
gibt, dort kostet der Sprit pro Liter den (geringeren) Betrag ![]() . Aber: Der Weg von
. Aber: Der Weg von ![]() nach Z über
nach Z über ![]() ist länger. Daraus erwächst unmittelbar die Frage, ob denn die Gesamtkosten beim Tanken an
ist länger. Daraus erwächst unmittelbar die Frage, ob denn die Gesamtkosten beim Tanken an ![]() tatsächlich um so vieles geringer sind als bei
tatsächlich um so vieles geringer sind als bei ![]() , dass unterm Strich, trotz der zu fahrenden Mehrstrecke, ein Vorteil bleibt?
, dass unterm Strich, trotz der zu fahrenden Mehrstrecke, ein Vorteil bleibt?
Zur Klarstellung: Selbstredend ist das alles nur eine theoretische Übung. Wenn man die tatsächlichen Betriebskosten eines Fahrzeugs zugrunde legt, die schon für einen Kompaktwagen mit Basismotorisierung bei 4-jähriger Haltedauer bei mehr als 40 ct/km liegen, dann braucht man mögliche Umwege gar nicht mehr ins Kalkül zu nehmen. Schon kurze Umwegstrecken über 2 – 3 km werden in der Regel alle Kostenvorteile durch billigeren Sprit aufzehren oder gar ins Gegenteil verkehren.
Nichtsdestotrotz: Die Skizze (s. Abbildung 1) zeigt die Zusammenhänge und Bezeichnungen.

Abbildung 1
Natürlich kann man das im konkreten Fall ganz einfach berechnen sofern alle relevanten Daten bekannt sind. Man nimmt die bekannten Preise ![]() und
und ![]() an den beiden Tankstellen, die in beiden Fällen zu fahrenden Teilstrecken
an den beiden Tankstellen, die in beiden Fällen zu fahrenden Teilstrecken ![]() und
und ![]() . Mit dem spezifischen Verbrauch pro Streckeneinheit
. Mit dem spezifischen Verbrauch pro Streckeneinheit ![]() , z.B. in
, z.B. in ![]() und der am Startort
und der am Startort ![]() im Tank befindlichen restlichen Spritmenge von
im Tank befindlichen restlichen Spritmenge von ![]() erhalten wir für die Gesamtkosten beim Tanken an Tankstelle
erhalten wir für die Gesamtkosten beim Tanken an Tankstelle ![]()
(1) ![]()
sowie die Gesamtkosten beim Tanken an Tankstelle ![]()
(2) ![]()
Der Umweg lohnt sich, wenn gilt
(3) ![]()
In der Regel kennt man aber die genauen Werte für die in der Rechnung benötigten Variablen nicht. Wie kann man trotzdem zu einer begründeten Entscheidung kommen?
Dazu betrachten wir die Ungleichung genauer und setzen für den Unterschied in der Streckenlänge ![]() (das ist der effektiv zu fahrende Umweg) sowie für die Preisdifferenz
(das ist der effektiv zu fahrende Umweg) sowie für die Preisdifferenz ![]() (das sind die Mehrkosten pro Liter an Tankstelle
(das sind die Mehrkosten pro Liter an Tankstelle ![]() gegenüber Tankstelle
gegenüber Tankstelle ![]() ). Wir erhalten nun die abgeleitete Bedingung
). Wir erhalten nun die abgeleitete Bedingung
(4) ![]()
woraus weiter folgt
(5) 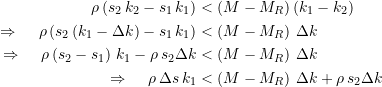
Wenn wir in dieser Ableitung die linke Seite von der rechten Seite subtrahieren erhalten wir direkt die Höhe der exakten Differenzkosten bzw. der potentiellen Ersparnis ![]() .
.
(6) 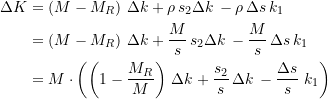
Nach dem Obigen ist das Rentabilitätskriterium ![]() auf jeden Fall dann erfüllt, wenn
auf jeden Fall dann erfüllt, wenn
(7) ![]()
Wir können davon ausgehen, dass die Länge der fraglichen Strecken ![]() und
und ![]() jeweils nur einen Bruchteil der gesamten mit einer Tankfüllung zurückzulegenden Fahrtstrecke
jeweils nur einen Bruchteil der gesamten mit einer Tankfüllung zurückzulegenden Fahrtstrecke ![]() ausmachen, sagen wir maximal 20%. Unter dieser Voraussetzung, also
ausmachen, sagen wir maximal 20%. Unter dieser Voraussetzung, also ![]() und
und ![]() , wird demnach das Kriterium maximal um den Wert
, wird demnach das Kriterium maximal um den Wert ![]() verschärft, dabei haben wir
verschärft, dabei haben wir ![]() verwendet.
verwendet.
Wenn wir für ![]() einfach
einfach ![]() schreiben und
schreiben und ![]() setzen, erhalten wir somit die prägnante Rentabilitätsbedingung
setzen, erhalten wir somit die prägnante Rentabilitätsbedingung
(8) ![]()
Das einfache Kriterium lautet demnach: Der Umweg lohnt sich, wenn der durch den Umweg hervorgerufene Mehrverbrauch ![]() in Relation zur fehlenden Füllmenge
in Relation zur fehlenden Füllmenge ![]() am Start kleiner ist, als das Verhältnis der Preisdifferenz pro Liter bezogen auf die regulären Kosten pro Liter.
am Start kleiner ist, als das Verhältnis der Preisdifferenz pro Liter bezogen auf die regulären Kosten pro Liter.
Hierin können wir wegen ![]() auch
auch ![]() einsetzen und bekommen so die modifizierte Form
einsetzen und bekommen so die modifizierte Form
(9) ![]()
Nach obiger Formel für den erzielten Gewinn ergibt sich im Grenzfall ![]() immer noch eine Ersparnis von
immer noch eine Ersparnis von
(10) 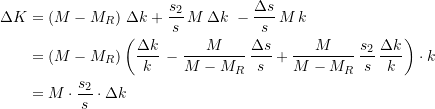
Das ist genau der Betrag, der in der Ableitung von Formel (7) vernachlässigt worden war.
In den meisten Fällen kennt man die nach Formel (8) benötigte Restmenge ![]() im Tank natürlich nicht genau, man kann sie aber mittels der Tankanzeige abschätzen. Eine andere Möglichkeit ist, stattdessen auf die oft sogar digital angezeigte Restreichweite
im Tank natürlich nicht genau, man kann sie aber mittels der Tankanzeige abschätzen. Eine andere Möglichkeit ist, stattdessen auf die oft sogar digital angezeigte Restreichweite ![]() auszuweichen. Wegen
auszuweichen. Wegen ![]() erhalten wir daher nach Ersetzen von
erhalten wir daher nach Ersetzen von ![]() in der vorstehenden Formel das einfacher zu handhabende Kriterium
in der vorstehenden Formel das einfacher zu handhabende Kriterium
(11) ![]()
Das modifizierte Kriterium lautet nun also: Der Umweg lohnt sich, wenn die Länge des Umwegs ![]() in Relation zur Differenz zwischen der Maximalreichweite
in Relation zur Differenz zwischen der Maximalreichweite ![]() und der Restreichweite
und der Restreichweite ![]() am Start kleiner ist, als das Verhältnis der Preisdifferenz pro Liter bezogen auf die regulären Kosten pro Liter.
am Start kleiner ist, als das Verhältnis der Preisdifferenz pro Liter bezogen auf die regulären Kosten pro Liter.
Wie oben erreicht auch hier die Ersparnis im Grenzfall ![]() den minimalen aber noch positiven Wert
den minimalen aber noch positiven Wert ![]() .
.
Das Kriterium kann man noch einfacher formulieren, wenn die Restmenge ![]() als klein gegenüber der maximalen Füllmenge
als klein gegenüber der maximalen Füllmenge ![]() angenommen wird, also
angenommen wird, also ![]() . In der Tat stellt sich die Frage, ob man denn nun tanken soll oder nicht, nur dann, wenn die Restmenge
. In der Tat stellt sich die Frage, ob man denn nun tanken soll oder nicht, nur dann, wenn die Restmenge ![]() unter einen bestimmten Füllstand gesunken ist. Für diese Grenze dürfen wir etwa 10% bis 20% der maximalen Füllmenge
unter einen bestimmten Füllstand gesunken ist. Für diese Grenze dürfen wir etwa 10% bis 20% der maximalen Füllmenge ![]() annehmen. Wenn also
annehmen. Wenn also ![]() , dann gilt
, dann gilt
(12) ![]()
womit weiter folgt
(13) ![]()
Wenn wir hier den zweiten Summanden weglassen, machen wir nach dem Vorstehenden einen Fehler höchstens in der Größe ![]() . Falls die Strecke
. Falls die Strecke ![]() sehr klein ist, also
sehr klein ist, also ![]() , und die Restmenge
, und die Restmenge ![]() im Tank relativ groß, also
im Tank relativ groß, also ![]() , würde auf der rechten Seite der Ungleichung der negative Summand
, würde auf der rechten Seite der Ungleichung der negative Summand ![]() fehlen. Für große Werte von
fehlen. Für große Werte von ![]() nahe
nahe ![]() könnten wir also die Rentabilitätsbedingung fälschlicherweise für erfüllt halten. Im umgekehrten Fall einer großen Strecke
könnten wir also die Rentabilitätsbedingung fälschlicherweise für erfüllt halten. Im umgekehrten Fall einer großen Strecke ![]() , also
, also ![]() , und einer kleinen Restmenge
, und einer kleinen Restmenge ![]() im Tank, also
im Tank, also ![]() , würde auf der rechten Seite der Ungleichung ein positiver Summand der Größe
, würde auf der rechten Seite der Ungleichung ein positiver Summand der Größe ![]() stehen. Für Werte von
stehen. Für Werte von ![]() größer als
größer als ![]() könnten wir also in dieser Situation die Rentabilitätsbedingung fälschlicherweise für nicht erfüllt halten. Praktisch haben diese Fälle keine Bedeutung, weil man das Kriterium im Sinne einer positiven Aussage natürlich nur dann heranziehen wird, wenn die Differenz zwischen der linken und der rechten Seite hinreichend groß ist, z.B.
könnten wir also in dieser Situation die Rentabilitätsbedingung fälschlicherweise für nicht erfüllt halten. Praktisch haben diese Fälle keine Bedeutung, weil man das Kriterium im Sinne einer positiven Aussage natürlich nur dann heranziehen wird, wenn die Differenz zwischen der linken und der rechten Seite hinreichend groß ist, z.B. ![]() .
.
Dies bedenkend können wir demnach den zweiten Summanden ignorieren und erhalten nach Division durch ![]() die knappe Form
die knappe Form
(14) ![]()
und somit die noch prägnantere Rentabilitätsbedingung
(15) ![]()
Das finale Kriterium lautet daher: Der Umweg lohnt sich, wenn die Länge des Umwegs in Relation zur gesamten mit einer Tankfüllung fahrbaren Strecke (Reichweite) kleiner ist, als das Verhältnis der Preisdifferenz pro Liter in Bezug auf die regulären Kosten pro Liter.
Wie groß ist die Ersparnis in dieser Situation? Das hängt von der Differenz zwischen ![]() und
und ![]() ab. Wir erhalten
ab. Wir erhalten
(16) 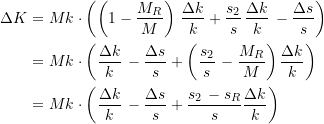
Somit bekommen wir im Grenzfall ![]() den Wert
den Wert
(17) 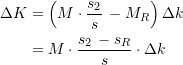
In diesem Extremfall ergibt sich also eine Ersparnis nur dann, wenn ![]() bzw., was dieselbe Aussage ist, wenn
bzw., was dieselbe Aussage ist, wenn ![]() . Für die Anwendung des Kriteriums haben wir
. Für die Anwendung des Kriteriums haben wir ![]() vorausgesetzt, demnach kann der Gewinn im ungünstigsten Falle bis auf den eventuell negativen Wert
vorausgesetzt, demnach kann der Gewinn im ungünstigsten Falle bis auf den eventuell negativen Wert
(18) ![]()
absinken. Diese negative Auszahlung können wir ganz leicht durch eine Modifikation des Kriteriums vermeiden. Wie man Gleichung (16) entnimmt reicht es dazu aus, für die Differenz ![]() einen Wert größer oder gleich
einen Wert größer oder gleich ![]() zu nehmen. Die im Grenzfall erzielte Einsparung wird damit
zu nehmen. Die im Grenzfall erzielte Einsparung wird damit
(19) 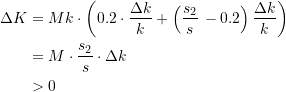
Demzufolge erhalten wir bei der erfüllten Bedingung
(20) ![]()
in jedem Falle eine positive Auszahlung. Der einfacheren Anwendung halber macht es Sinn, das Kriterium in die Form
(21) ![]()
zu bringen und dergestalt nochmals zu verschärfen („Halbe-Regel“). Ist diese Bedingung erfüllt, können wir sicher sein, dass der Kostenvorteil beim Tanken an ![]() durch die Umwegstrecke höchstens teilweise aufgezehrt wird. Auch im ungünstigen Fall einer kurzen Strecke
durch die Umwegstrecke höchstens teilweise aufgezehrt wird. Auch im ungünstigen Fall einer kurzen Strecke ![]() und einer hohen Restmenge
und einer hohen Restmenge ![]() im Tank, bliebe noch ein Kostenvorteil von mindestens 30% der Bruttoersparnis auf Basis der reinen Tankkosten. Das kann man unmittelbar beim Einsetzen in Gleichung (19) ableiten:
im Tank, bliebe noch ein Kostenvorteil von mindestens 30% der Bruttoersparnis auf Basis der reinen Tankkosten. Das kann man unmittelbar beim Einsetzen in Gleichung (19) ableiten:
(22) 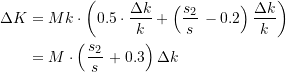
Verweilen wir noch einen Moment bei der Bestimmung des resultierenden Kostenvorteils. Mit den Gleichungen (1) und (16) können wir den effektiven relativen Kostenvorteil in Abhängigkeit vom Erfüllungsgrad des Kriterium errechnen. Wir erhalten (mit ![]() ,
, ![]() sowie
sowie ![]() )
)
(23) 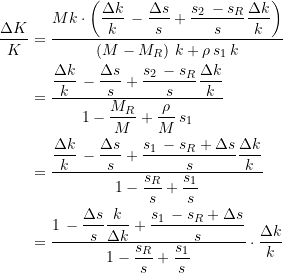
Wenn wir nun im Sinne des obigen Kriteriums allgemein
(24) ![]()
mit ![]() setzen und
setzen und ![]() mit
mit ![]() vereinbaren, so können wir den Ausdruck umformen zu
vereinbaren, so können wir den Ausdruck umformen zu
(25) 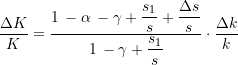
Demnach bekommen wir für die relative Ersparnis zunächst
(26) ![]()
und sofern ![]() , wenn also die Restreichweite
, wenn also die Restreichweite ![]() größer als
größer als ![]() ist,
ist,
(27) ![]()
Je kleiner die relative Länge des Umwegs ![]() im Vergleich zur relativen Preisdifferenz pro Liter
im Vergleich zur relativen Preisdifferenz pro Liter ![]() ist (das genau ist die Bedeutung der Größe
ist (das genau ist die Bedeutung der Größe ![]() ) und je kleiner die Restreichweite
) und je kleiner die Restreichweite ![]() im Vergleich zur regulären Reichweite
im Vergleich zur regulären Reichweite ![]() ist (also
ist (also ![]() ), desto näher liegt die aufgrund der örtlichen Gegebenheiten und dem Tankfüllstand tatsächlich realisierbare relative Kosteneinsparung an der relativen Preisdifferenz pro Liter.
), desto näher liegt die aufgrund der örtlichen Gegebenheiten und dem Tankfüllstand tatsächlich realisierbare relative Kosteneinsparung an der relativen Preisdifferenz pro Liter.
Im Falle der Halbe-Regel (also ![]() ) heißt dies konkret
) heißt dies konkret
(28) 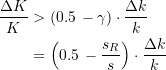
Unter der oben formulierten Voraussetzung ![]() , was ja zugleich
, was ja zugleich ![]() bedeutet, folgt unmittelbar
bedeutet, folgt unmittelbar
(29) ![]()
Mindestens 30% des maximal möglichen Gewinns werden daher bei erfüllter Halbe-Regel realisiert. In absoluten Größen hatten wird das schon oben formuliert.
Das Rentabilitätskriterium können wir zur Berechnung der höchstens sinnvollen Länge des Umwegs verwenden. Nach Obigem haben wir
(30) ![]()
bzw. die konservativere Abschätzung (Halbe-Regel)
(31) ![]()
oder kürzer
(32) ![]()
Den exakten Wert für die maximal sinnvolle Länge des Umwegs erhält man aus Formel (5) wegen
(33) 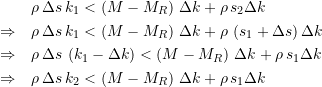
und mit ![]() zu
zu
(34) 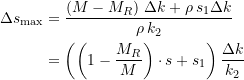
In der nachfolgenden Tabelle sind einige Beispiele durchgerechnet:
| Beispielkalkulation | A | B | C | D |
| *Preis | 1,25 | 1,25 | 1,12 | 1,32 |
| Preis | 1,20 | 1,20 | 1,04 | 1,26 |
| *Preisdifferenz | 5 | 5 | 8 | 6 |
| Fahrtstrecke | 10 | 10 | 10 | 20 |
| Fahrtstrecke | 20 | 30 | 30 | 25 |
| Tankgröße | 48 | 48 | 72 | 42 |
| Restmenge | 6 | 24 | 8 | 7 |
| *Umweg | 10 | 20 | 20 | 5 |
| *Reichweite | 800 | 800 | 1200 | 600 |
| Gesamtkosten | 53,25 | 30,75 | 72,35 | 48,05 |
| Gesamtkosten | 51,84 | 30,96 | 68,43 | 46,31 |
Tabelle 1a
| Beispielkalkulation | A | B | C | D |
| Ersparnis | 1,41 | -0,21 | 3,92 | 1,74 |
| Kriterium | 0,014 < 0,04 | 0,05 < 0,04 | 0,019 < 0,071 | 0,01 < 0,045 |
| Kriterium | 0,013 < 0,04 | 0,025 < 0,04 | 0,017 < 0,071 | 0,008 < 0,045 |
| Kriterium | 0,025 < 0,04 | 0,05 < 0,04 | 0,033 < 0,071 | 0,017 < 0,045 |
| Maximal empfohlener Umweg | 16,00 | 16,00 | 42,86 | 13,64 |
| Ersparnis | 0,98 | 0,08 | 2,49 | 0,98 |
| Maximal sinnvoller Umweg in km | 29,58 | 17,08 | 82,82 | 24,76 |
Tabelle 1b
Anmerkung: Für die Anwendung des Kriteriums braucht man nur die in der Tabelle mit einem Stern (*) markierten Werte.
In den gewählten Beispielen A, C und D lohnen sich die Umwege mit den angegebenen Ersparnissen von 1,41 €, 3,92 € und 1,74 €. Alle drei Kriterien, das Restmengenkriterium, das einfache finale Kriterium sowie die Halbe-Regel geben dazu jeweils die richtige Einschätzung. Im Falle von Beispiel B mit der großen Restmenge im Tank liegt das einfache finale Kriterium hingegen falsch: Folgt man ihm, so würde man den Umweg fahren, letztlich aber draufzahlen (Mehrausgabe = 0,21 €). Ursächlich hierfür ist die nicht erfüllte Anwendungsbedingung ![]() . Das Restmengenkriterium und die Halbe-Regel liegen indessen auch in diesem Falle richtig und empfehlen den Umweg nicht.
. Das Restmengenkriterium und die Halbe-Regel liegen indessen auch in diesem Falle richtig und empfehlen den Umweg nicht.
Die obigen Beispiele repräsentieren typische Einzelfälle. Interessanter ist die Frage nach dem möglichen Gewinn bei konsequenter Befolgung der Kriterien. Dazu betrachten wir die mögliche Einsparung im Falle der obigen Beispiele bezogen auf unterschiedliche Jahresfahrleistungen und ausgehend von Annahmen über die Variationsbreite der Spritpreise, der Preisdifferenz, der Restfüllmenge im Tank, der Fahrstrecke zwischen Start und Ziel sowie der Länge des Umwegs. In Tabelle 2 sind für vier Beispiele jeweils die angenommenen minimalen und maximalen Werte aufgelistet. Die resultierenden Ergebnisse unter der Annahme einer Gleichverteilung innerhalb der angegebenen Spannbreiten sind in Tabelle 3 als Fazit aus Monte-Carlo-Simulationen für jeweils 1000 Tankfahrten mit zufällig variierten Eingangsparametern pro Beispiel dokumentiert. In Tabelle 4 sind die daraus abgeleiteten Resultate für die mittleren Einsparungen bei den gegebenen Jahresfahrleistungen für die vier Beispiele aufgelistet.
| Parametervariation | A | B | C | D |
| Minimaler Preis | 1,2 | 1,22 | 0,95 | 1,22 |
| Maximaler Preis | 1,4 | 1,45 | 1,2 | 1,5 |
| Unterer Wert der Preisdifferenz | 1 | 1 | 1 | 1 |
| Oberer Wert der Preisdifferenz | 10 | 10 | 10 | 10 |
| Minimaler Wert für die Fahrtstrecke | 10 | 10 | 10 | 10 |
| Maximaler Wert für die Fahrtstrecke | 30 | 30 | 30 | 30 |
Tabelle 2a
| Parametervariation | A | B | C | D |
| Minimaler Wert für die Fahrtstrecke | 10 | 10 | 10 | 10 |
| Maximaler Wert für die Fahrtstrecke | 30 | 30 | 30 | 30 |
| Minimaler Umweg | 1 | 1 | 1 | 1 |
| Maximaler Umweg | 20 | 20 | 30 | 10 |
| Unterer Wert für die Restmenge im Tank | 3 | 3 | 3 | 3 |
| Oberer Wert für die Restmenge im Tank | 10 | 24 | 16 | 10 |
Tabelle 2b
Nach den vorstehenden Daten wird unterstellt, dass sich die Preisdifferenz zwischen 1 und 10 Cent bewegt. Im Mittel liegt der Unterschied somit bei etwa 5 ct.
| Monte-Carlo Simulation – Übersicht | A | B | C | D |
| Anzahl Fahrten | 1000 | 1000 | 1000 | 1000 |
| Anteil Fahrten mit Gewinn | 0,859 | 0,811 | 0,901 | 0,910 |
| Anteil Fahrten ohne Gewinn | 0,141 | 0,189 | 0,099 | 0,090 |
| Summe Gewinne | 1376,73 | 1054,47 | 2267,59 | 1349,53 |
| Mittelwert Gewinn pro Tankvorgang | 1,377 | 1,054 | 2,268 | 1,350 |
| Monte-Carlo Simulation | A | B | C | D |
| Anzahl Fahrten mit erfülltem Kriterium unter Berücksichtigung des Tankfüllstandes | 851 | 793 | 895 | 906 |
| Anteil solcher Fahrten | 0,851 | 0,793 | 0,895 | 0,906 |
| Anteil Fahrten mit Gewinn | 1,000 | 1,000 | 1,000 | 1,000 |
| Anteil Fahrten ohne Gewinn | 0,000 | 0,000 | 0,000 | 0,000 |
| Summe Gewinne | 1436,28 | 1136,25 | 2319,50 | 1367,71 |
| Mittelwert Gewinn pro Tankvorgang | 1,688 | 1,433 | 2,592 | 1,510 |
| Monte-Carlo Simulation | A | B | C | D |
| Anzahl Fahrten mit erfülltem einfachen Kriterium | 874 | 880 | 916 | 928 |
| Anteil solcher Fahrten | 0,874 | 0,880 | 0,916 | 0,928 |
| Anteil Fahrten mit Gewinn | 0,983 | 0,922 | 0,984 | 0,981 |
| Anteil Fahrten ohne Gewinn | 0,017 | 0,078 | 0,016 | 0,019 |
| Summe Gewinne | 1435,65 | 1126,09 | 2318,57 | 1366,82 |
| Mittelwert Gewinn pro Tankvorgang | 1,643 | 1,280 | 2,531 | 1,473 |
| Monte-Carlo Simulation | A | B | C | D |
| Anzahl Fahrten mit erfüllter Halbe-Regel | 685 | 681 | 763 | 812 |
| Anteil solcher Fahrten | 0,685 | 0,682 | 0,763 | 0,812 |
| Anteil Fahrten mit Gewinn | 1,000 | 1,000 | 1,000 | 1,000 |
| Anteil Fahrten ohne Gewinn | 0,000 | 0,000 | 0,000 | 0,000 |
| Summe Gewinne | 1356,54 | 1093,10 | 2250,26 | 1346,75 |
| Mittelwert Gewinn pro Tankvorgang | 1,980 | 1,605 | 2,949 | 1,659 |
| Monte-Carlo Simulation | A | B | C | D |
| Anzahl Fahrten mit erfülltem exaktem Kriterium | 859 | 811 | 901 | 910 |
| Anteil solcher Fahrten | 0,859 | 0,811 | 0,901 | 0,910 |
| Anteil Fahrten mit Gewinn | 1,000 | 1,000 | 1,000 | 1,000 |
| Anteil Fahrten ohne Gewinn | 0,000 | 0,000 | 0,000 | 0,000 |
| Summe Gewinne | 1436,57 | 1136,81 | 2319,65 | 1367,76 |
| Mittelwert Gewinn pro Tankvorgang | 1,672 | 1,402 | 2,575 | 1,503 |
Tabelle 3
| Mittlere Einsparung (Halbe-Regel) | A | B | C | D |
| Jahresfahrleistung in km | 20000 | 20000 | 30000 | 10000 |
| Mittlere Fahrstrecke pro Tankfüllung in km | 700 | 585 | 1052 | 512 |
| Anzahl Tankvorgänge pro Jahr | 28,56 | 34,18 | 28,53 | 19,54 |
| Resultierende Ersparnis im Jahr in € bei Anwendung der Halbe-Regel | 39,06 | 36,27 | 64,70 | 28,03 |
Tabelle 4
Die mittleren Fahrstrecken pro Tankfüllung ergeben sich aus den variierten Restfüllständen nach Tabelle 2 gemäß den unterstellten unteren und oberen Grenzen. Die Anzahl der Tankvorgänge pro Jahr folgt aus der Jahresfahrleistung und der mittleren Fahrstrecke pro Füllung.
Der vorstehenden Tabelle entnimmt man auf Basis der angegebenen Jahresfahrleistungen und den in Tabelle 2 dokumentierten Variationsbreiten für die Spritkosten, die Preisdifferenz und die zu fahrenden Umwege mittlere Einsparpotentiale in der Größenordnung der Kosten für etwa eine halbe Tankfüllung.


