Wir diskutieren im Folgenden spezielle Eigenschaften von Monomen der Art ![]() mit
mit ![]() bzw.
bzw. ![]() mit
mit ![]() , insbesondere betrachten wir die Kurvenkrümmung und den Krümmungsradius. In Abbildung 1 sind exemplarisch die drei Monome
, insbesondere betrachten wir die Kurvenkrümmung und den Krümmungsradius. In Abbildung 1 sind exemplarisch die drei Monome ![]() ,
, ![]() und
und ![]() mit der Lage der entsprechenden minimalen Krümmungskreisen dargestellt.
mit der Lage der entsprechenden minimalen Krümmungskreisen dargestellt.
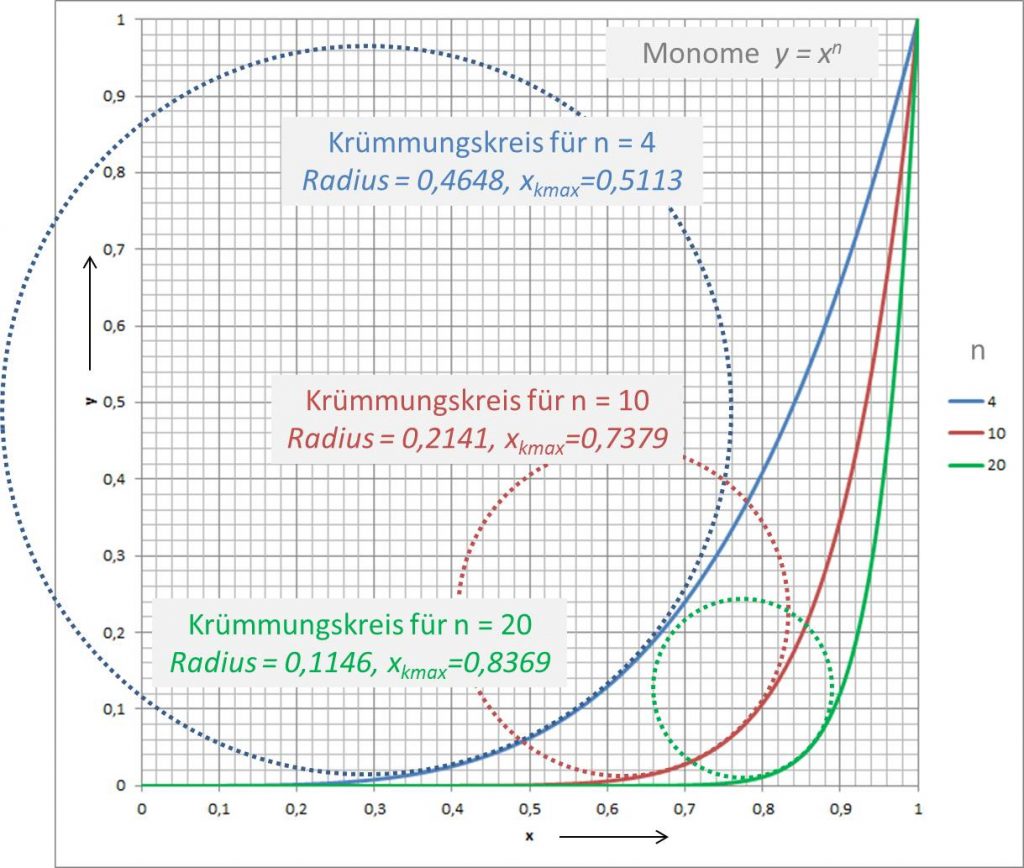
Abbildung 1
Die Kurve des Monoms ![]() hat ihre maximale Krümmung
hat ihre maximale Krümmung ![]() an der Position
an der Position
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} x = x^{(n)}\mid_{k=\text{max}} &= \pm \, \sqrt[{2n-2}]{\dfrac{n-2}{a^2n^2(2n-1)}} \\ &= \pm \, {\left({\dfrac{1}{an}\sqrt{\dfrac{n-2}{2n-1}}}\right)}^{\frac{1}{n-1}} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-f7672d100e78bf4473399aa7bf2eeac5_l3.png)
Die Krümmung ![]() selbst nimmt den Wert
selbst nimmt den Wert
(2) 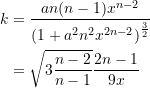
an, wobei hier der obige positive Wert von ![]() einzusetzen ist.
einzusetzen ist.
Im Grenzfall ![]() ist
ist ![]() und die Krümmung nimmt den Wert
und die Krümmung nimmt den Wert ![]() an. Für das Monom
an. Für das Monom ![]() ergibt sich also die maximale Krümmung im Punkt
ergibt sich also die maximale Krümmung im Punkt ![]() mit
mit ![]() und somit der minimale Krümmungsradius zu
und somit der minimale Krümmungsradius zu ![]() .
.
Ohne Bezug auf ![]() kann man die Krümmung direkt mit der folgenden Formel bestimmen
kann man die Krümmung direkt mit der folgenden Formel bestimmen
(3) 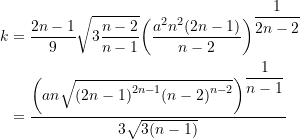
Mit wachsendem Exponenten ![]() wandern die Punkte maximaler Krümmung auf den Kurven
wandern die Punkte maximaler Krümmung auf den Kurven ![]() von
von ![]() für
für ![]() bis
bis ![]() für
für ![]() . Der Zusammenhang ist in Abbildung 2 dargestellt.
. Der Zusammenhang ist in Abbildung 2 dargestellt.
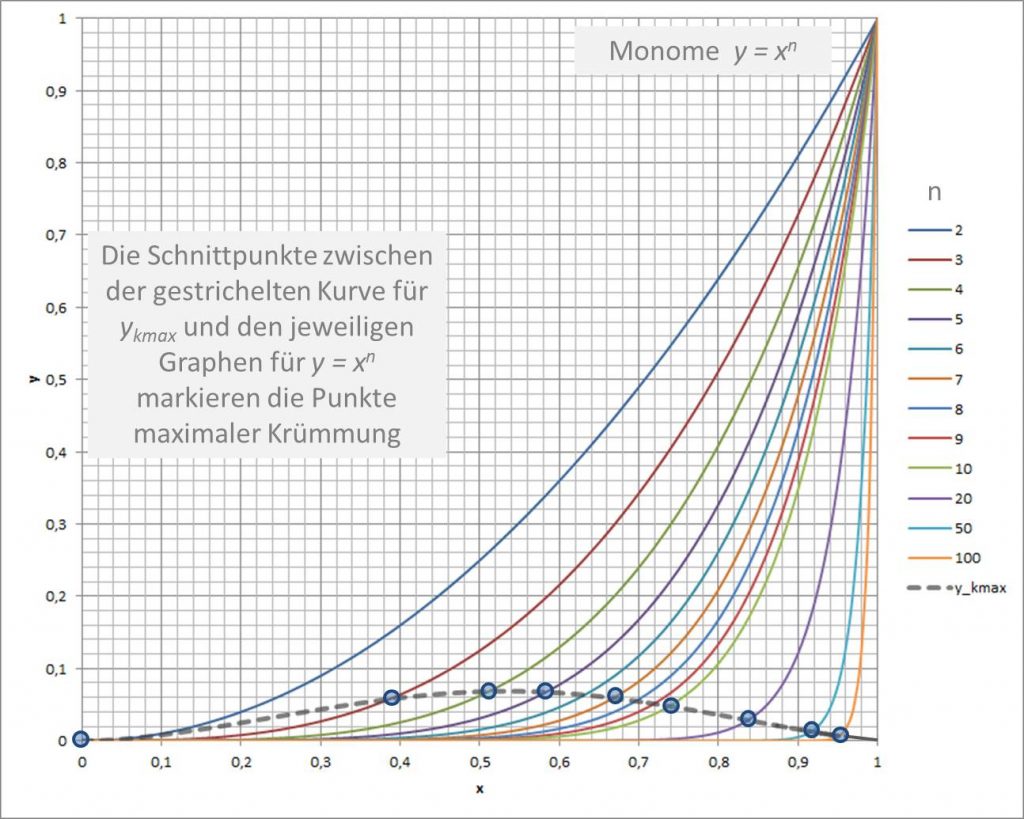
Abbildung 2
Die Trajektorie des Punktes der maximalen Krümmung ![]() der Kurve
der Kurve ![]() bei Variation von
bei Variation von ![]() von
von ![]() bis
bis ![]() für positive Werte von
für positive Werte von ![]() ist in der nachfolgenden Grafik vergrößert dargestellt.
ist in der nachfolgenden Grafik vergrößert dargestellt.
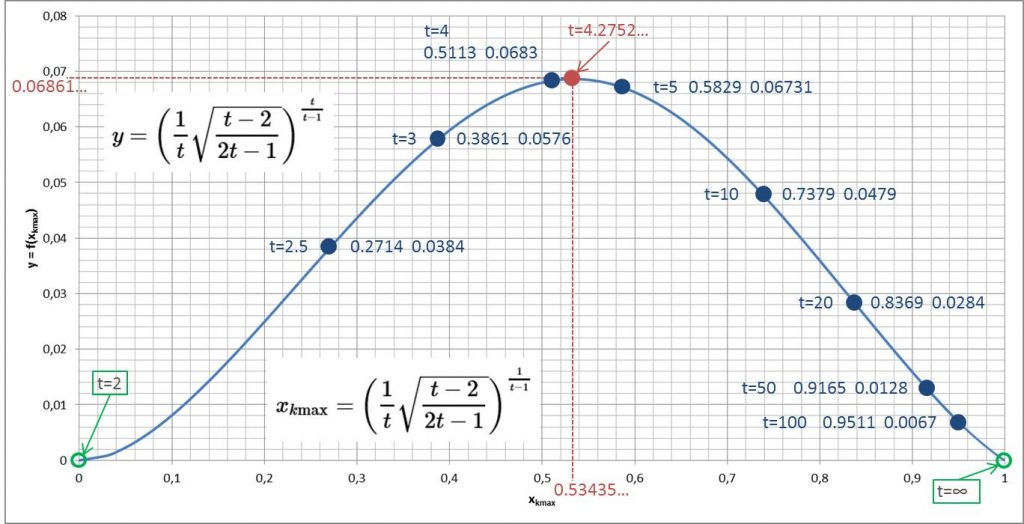
Abbildung 3
Für den Exponenten ![]() nimmt
nimmt ![]() den maximalen Wert von
den maximalen Wert von ![]() an, zugleich ist
an, zugleich ist ![]() .
.
Interessant ist die Frage nach dem Verhalten dieses Graphen am linken und am rechten Rand des Definitionsbereichs. Betrachten wir zunächst einmal die Umgebung von ![]() und setzen hierfür
und setzen hierfür ![]() :
:
(4) 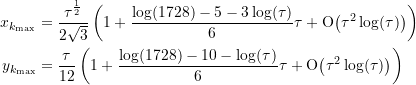
Demnach gilt also für kleine ![]() die Näherungsformel
die Näherungsformel
(5) ![]()
Tatsächlich erhalten wir für die Ableitung
(6) 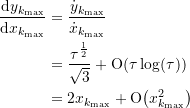
für ![]() .
.
Aus den beiden obigen Approximationen folgt zwanglos
(7) 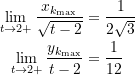
Am anderen Ende, also für ![]() , geht
, geht ![]() ebenfalls gegen
ebenfalls gegen ![]() während
während ![]() strebt. Der Graph erweckt dabei den Anschein, als ob die Trajektorie die
strebt. Der Graph erweckt dabei den Anschein, als ob die Trajektorie die ![]() -Achse unter einem positiven Winkel scheiden würde. Das ist indes nicht zutreffend. Stattdessen haben wir in diesem Fall die Näherung
-Achse unter einem positiven Winkel scheiden würde. Das ist indes nicht zutreffend. Stattdessen haben wir in diesem Fall die Näherung
(8) ![]()
Demnach gilt also ![]() für
für ![]() .
.
Generell beschreiben die beiden Näherungsformeln
(9) 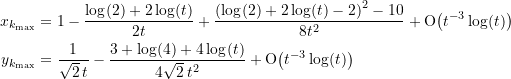
das Verhalten des Graphen von ![]() für große Exponenten
für große Exponenten ![]() . Insbesondere folgt hieraus
. Insbesondere folgt hieraus
(10) ![]()
sowie
(11) ![]()
Kommen wir nun zum Krümmungsradius ![]() . Aus Formel (3) resultiert unmittelbar die folgende Formel
. Aus Formel (3) resultiert unmittelbar die folgende Formel
(12) 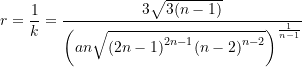
In Abbildung 4 ist der Verlauf ![]() für
für ![]() dargestellt.
dargestellt.
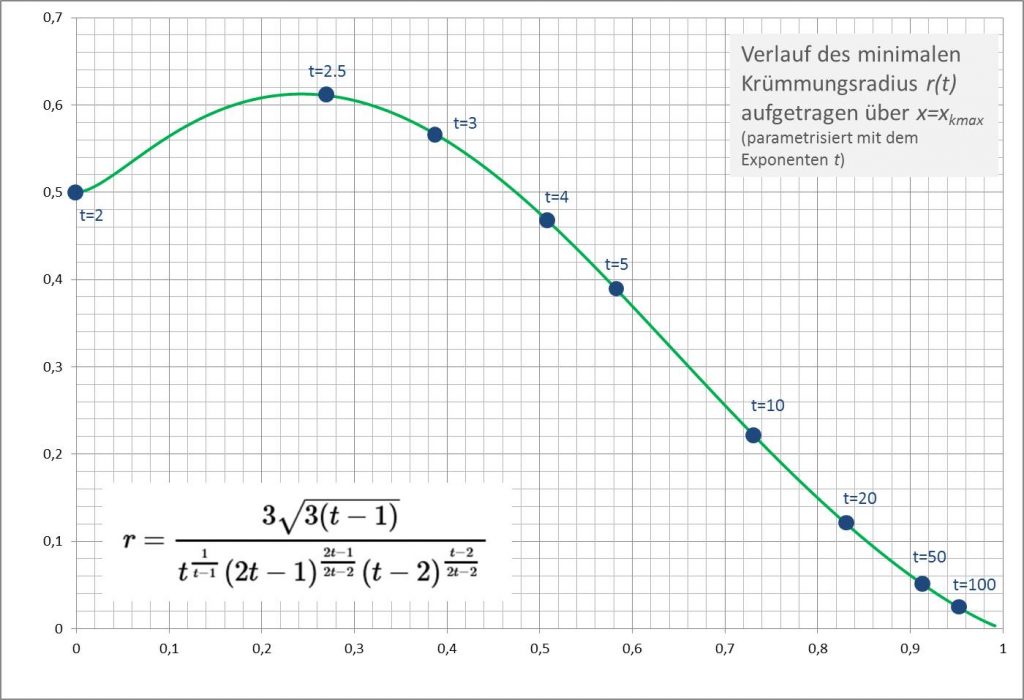
Abbildung 4
Es fällt auf, dass der minimale Krümmungsradius eines Monoms ![]() für Exponenten
für Exponenten ![]() zunächst einmal über den initialen Wert von
zunächst einmal über den initialen Wert von ![]() hinauswächst und bei
hinauswächst und bei ![]() ein Maximum erreicht. Der Ausgangswert wird erst wieder bei
ein Maximum erreicht. Der Ausgangswert wird erst wieder bei ![]() (genauer:
(genauer: ![]() ) unterschritten. Das verwundert! Intuitiv hätte man mit wachsendem Exponenten eine ebenfalls wachsende maximale Krümmung auf der Kurve
) unterschritten. Das verwundert! Intuitiv hätte man mit wachsendem Exponenten eine ebenfalls wachsende maximale Krümmung auf der Kurve ![]() und damit einen sich gleichmäßig reduzierenden minimalen Krümmungsradius erwartet.
und damit einen sich gleichmäßig reduzierenden minimalen Krümmungsradius erwartet.
Ein genauerer Wert für den Exponenten, bei dem das Maximum des minimalen Krümmungsradius erreicht wird, ist ![]() . Der zugehörige Krümmungsradius ist
. Der zugehörige Krümmungsradius ist ![]() . Dazu korrespondieren
. Dazu korrespondieren ![]() und
und ![]() als die entsprechenden
als die entsprechenden ![]() – und
– und ![]() -Werte des Punktes der maximalen Krümmung auf der Kurve des Monoms
-Werte des Punktes der maximalen Krümmung auf der Kurve des Monoms ![]() .
.
Auch hier kann man wieder nach dem Verhalten für kleine und große Exponenten ![]() fragen.
fragen.
Bei kleinen Exponenten ![]() erhalten wir die folgende Näherung
erhalten wir die folgende Näherung
(13) ![]()
wobei
(14) ![]()
In Abbildung 4 ist der Graph von ![]() dargestellt. In der Nähe des Punktes
dargestellt. In der Nähe des Punktes ![]() erhält man für die Steigung der Kurve
erhält man für die Steigung der Kurve
(15) 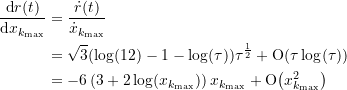
Demnach haben wir also ![]() für
für ![]() bzw. für
bzw. für ![]() .
.
Aus der vorstehenden Näherungsformel zu ![]() ergibt sich mittels Integration die folgende Abschätzung für den Krümmungsradius
ergibt sich mittels Integration die folgende Abschätzung für den Krümmungsradius ![]() in Abhängigkeit von
in Abhängigkeit von ![]()
(16) ![]()
Zum gleichen Ergebnis gelangt man durch den direkten Vergleich der oben formulierten Näherungen für ![]() und
und ![]() . Für
. Für ![]() (das ist zutreffend für Exponenten
(das ist zutreffend für Exponenten ![]() ) bleibt der Schätzfehler unterhalb von
) bleibt der Schätzfehler unterhalb von ![]() , für
, für ![]() (das ist zutreffend für Exponenten
(das ist zutreffend für Exponenten ![]() ) ist
) ist ![]() .
.
Aus dem Obigen resultieren die beiden Grenzwerte
(17) ![]()
und
(18) ![]()
Nun zur Analyse für ![]() . Hier erhalten wir die Approximation
. Hier erhalten wir die Approximation
(19) ![]()
Damit ist also
(20) ![]()
In Abbildung 5b sind beide Achsen logarithmisch dargestellt, hier erkennt man den Charakter der vorstehend formulierten Näherung unmittelbar.
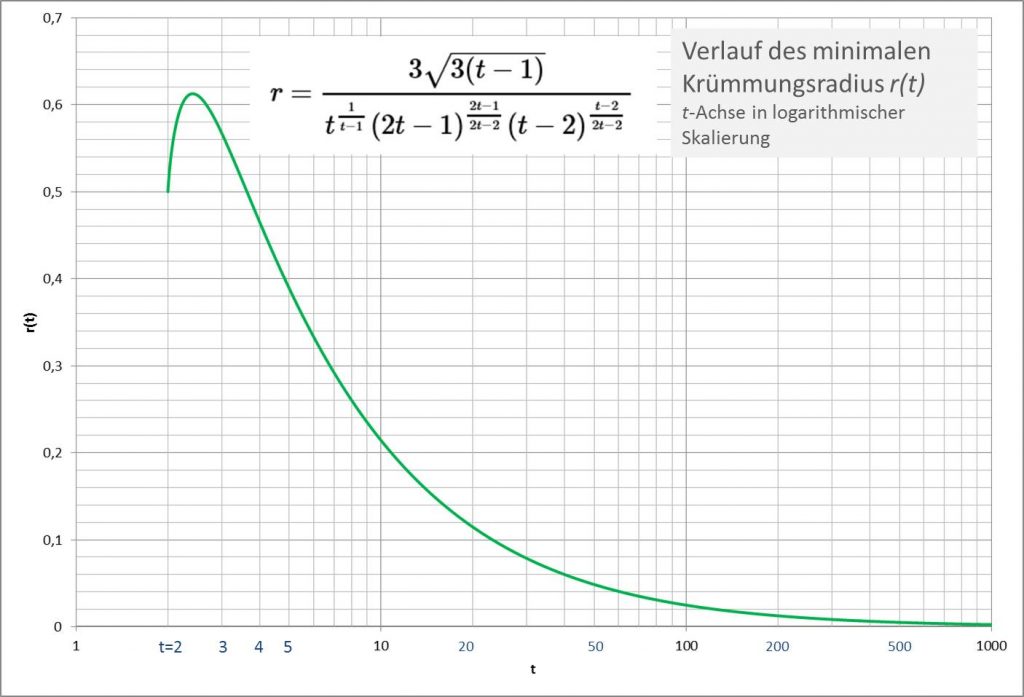
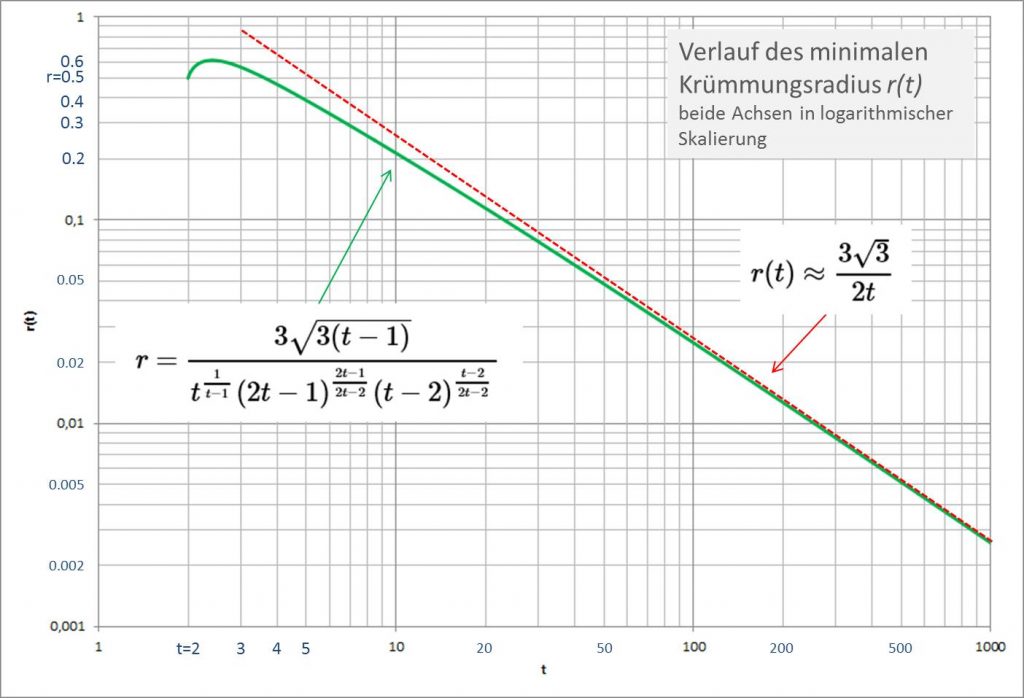
Abbildung 5a/b
Im folgenden betrachten wir die Trajektorie der Krümmungskreismittelpunkte ![]() . Die Konstruktion der entsprechenden Punkte ist in Abbildung 6 am Beispiel des Exponenten
. Die Konstruktion der entsprechenden Punkte ist in Abbildung 6 am Beispiel des Exponenten ![]() dargestellt.
dargestellt.
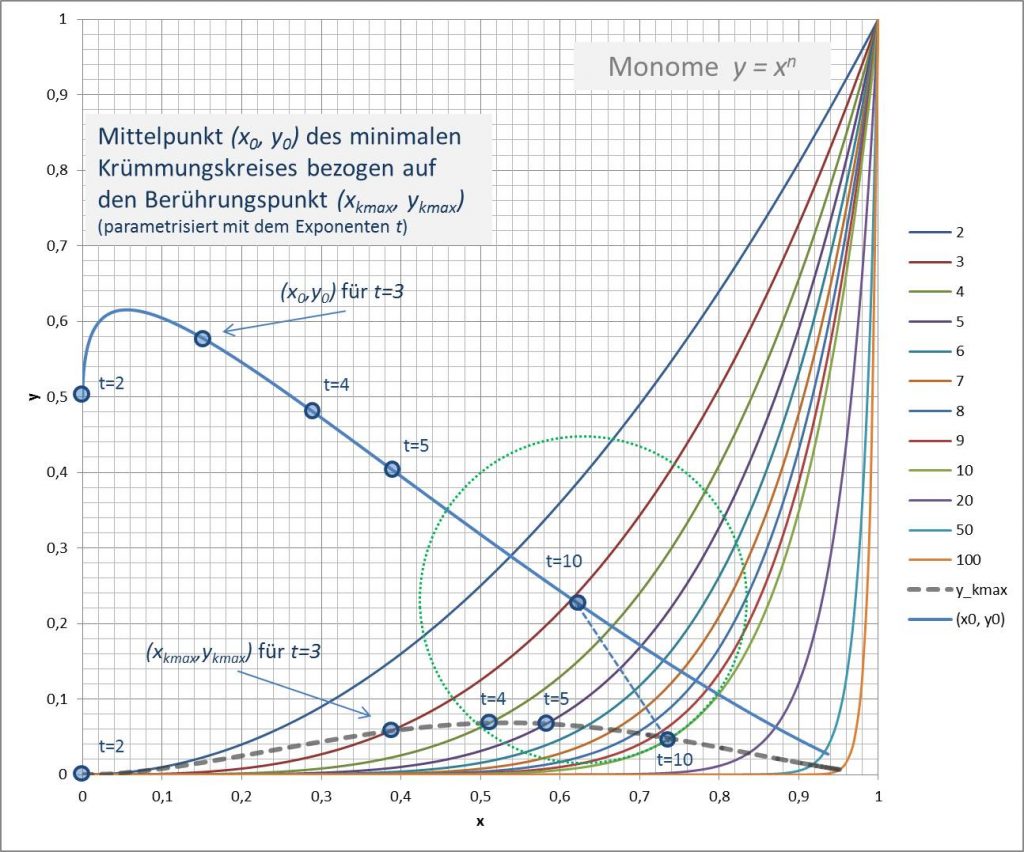
Abbildung 6
Für zwei weitere Beispiele von Krümmungskreisen bezogen auf die Exponenten ![]() und
und ![]() s. Abbildung 7.
s. Abbildung 7.
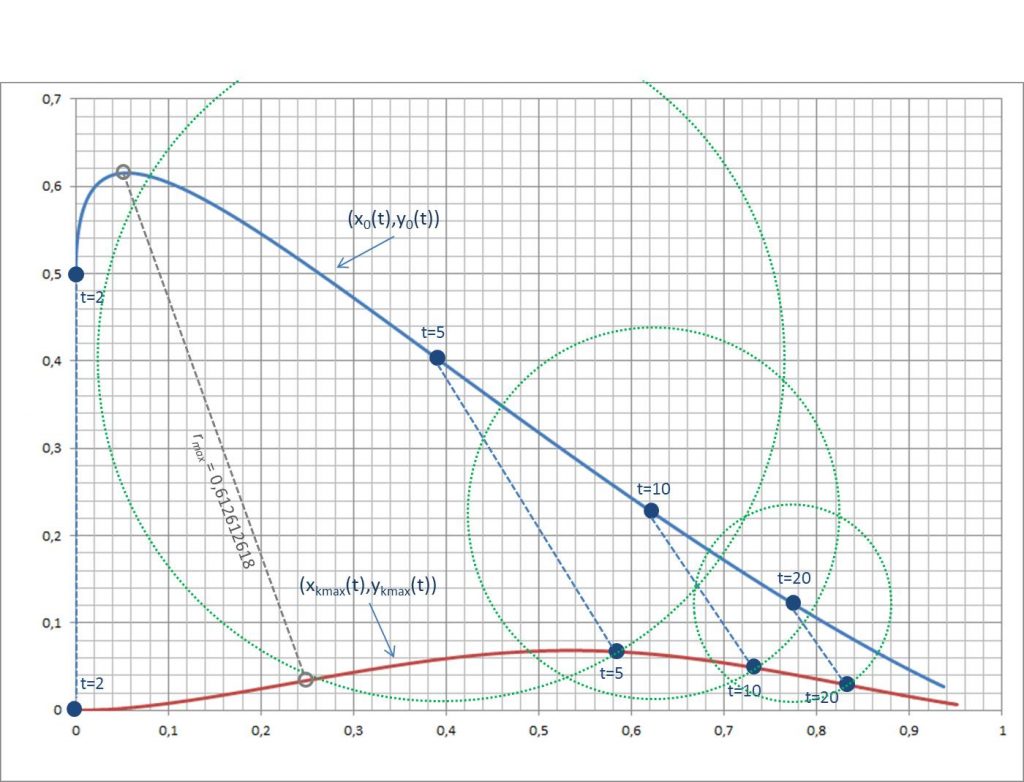
Abbildung 7
Die Positionen ![]() werden aus den
werden aus den ![]() und dem entsprechenden Krümmungsradius
und dem entsprechenden Krümmungsradius ![]() folgendermaßen berechnet:
folgendermaßen berechnet:
(21) 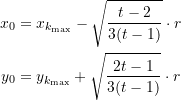
Die Näherungsausdrücke für ![]() sind
sind
(22) 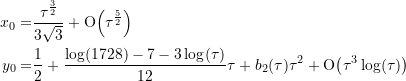
wobei
(23) ![]()
Aus den vorstehenden Ausdrücken folgen unmittelbar die beiden Limites
(24) 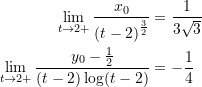
Für kleine Werte von ![]() erhalten wir zudem die folgende Approximation
erhalten wir zudem die folgende Approximation
(25) ![]()
und somit den Limes
(26) ![]()
Weiter erhält man für ![]()
(27) 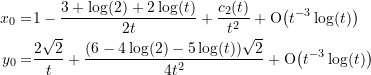
wobei
(28) ![]()
Die Grenzwerte für ![]() bzw.
bzw. ![]() ergeben sich zu
ergeben sich zu
(29) ![]()
sowie
(30) ![]()
Interessant ist noch die Betrachtung des Verlaufs des Winkels ![]() der Steigung der Kurve
der Steigung der Kurve ![]() am Punkt der maximalen Krümmung. Für
am Punkt der maximalen Krümmung. Für ![]() ist dieser Winkel
ist dieser Winkel ![]() . Mit wachsendem Exponenten wird der Winkel steiler und wächst schnell zu Werten über
. Mit wachsendem Exponenten wird der Winkel steiler und wächst schnell zu Werten über ![]() hin. Vom Augenschein her (z.B. von Abbildung 6) ist es zunächst aber dennoch unklar, wie sich der Winkel bei größeren Werten von
hin. Vom Augenschein her (z.B. von Abbildung 6) ist es zunächst aber dennoch unklar, wie sich der Winkel bei größeren Werten von ![]() verhält. Wir brauchen die Ableitung von
verhält. Wir brauchen die Ableitung von ![]() für
für ![]() und greifen dazu auf Formel (1) zurück.
und greifen dazu auf Formel (1) zurück.
(31) 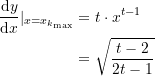
Abbildung 8 zeigt die Steigung der Kurve ![]() am Punkt der maximalen Krümmung in Abhängigkeit von
am Punkt der maximalen Krümmung in Abhängigkeit von ![]() .
.
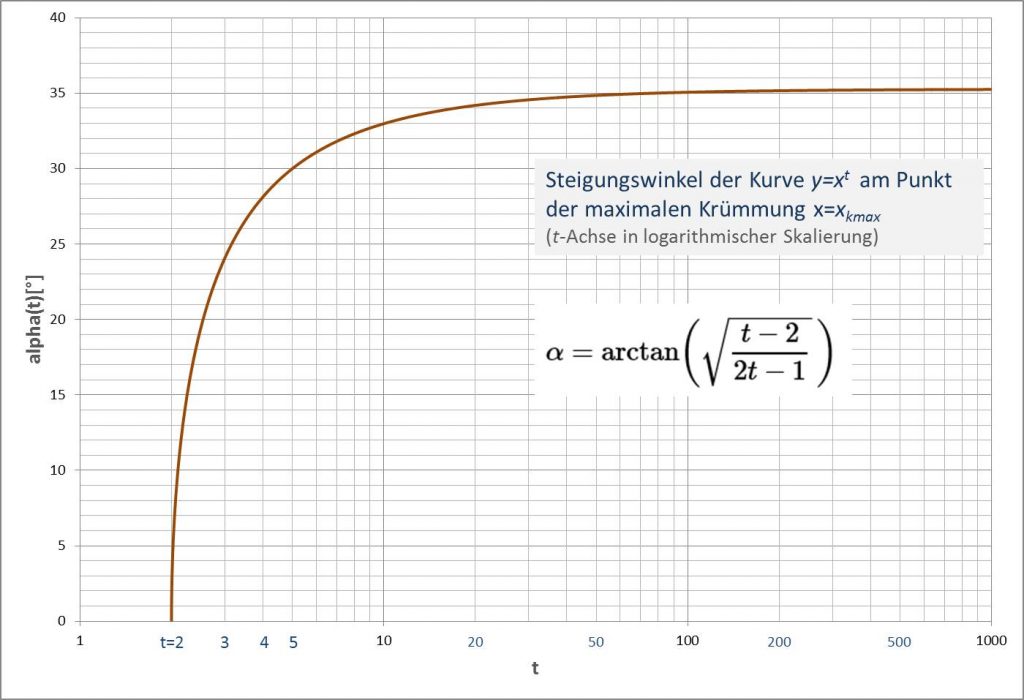
Abbildung 8
Abbildung 9 zeigt den Verlauf des Steigungswinkels in Abhängigkeit von der Position ![]() und parametrisiert mit
und parametrisiert mit ![]() .
.
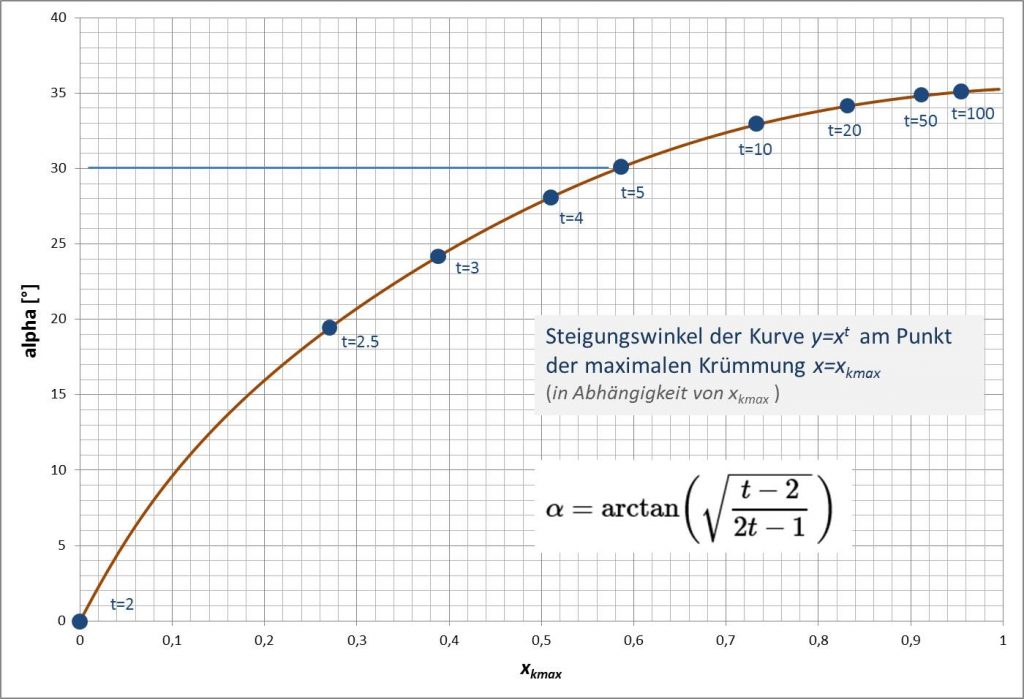
Abbildung 9
Für kleine Werte von ![]() ergibt sich für
ergibt sich für ![]() die folgende Näherungsformel
die folgende Näherungsformel
(32) ![]()
Die Steigung ![]() ist für
ist für ![]() gleich
gleich ![]() , steigt mit
, steigt mit ![]() aber rasch an. Betrachtet man die Abhängigkeit von der Position
aber rasch an. Betrachtet man die Abhängigkeit von der Position ![]() der maximalen Krümmung (s. Abbildung 9), so findet man für
der maximalen Krümmung (s. Abbildung 9), so findet man für ![]() den Näherungsausdruck
den Näherungsausdruck
(33) ![]()
und damit auch ![]() . Der Steigungswinkel
. Der Steigungswinkel ![]() wächst daher für kleine
wächst daher für kleine ![]() anfänglich mit eine Rate von
anfänglich mit eine Rate von ![]() . In Abbildung 9 kann man das gut erkennen.
. In Abbildung 9 kann man das gut erkennen.
Für ![]() lautet die Approximation
lautet die Approximation
(34) ![]()
Demnach strebt die Steigung der Kurve ![]() am Punkt der maximalen Krümmung für
am Punkt der maximalen Krümmung für ![]() gegen den Wert
gegen den Wert ![]() , also
, also
(35) ![]()
Für den Steigungswinkel heißt das
(36) 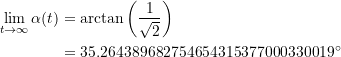
Der Verbindungsstrahl zwischen dem Mittelpunkt ![]() des Krümmungskreises und dem zugeordneten Punkt der maximalen Krümmung
des Krümmungskreises und dem zugeordneten Punkt der maximalen Krümmung ![]() steht senkrecht über der Kurve des Monoms
steht senkrecht über der Kurve des Monoms ![]()
Der Winkel ![]() der Normalen auf der Kurve
der Normalen auf der Kurve ![]() am Punkt der maximalen Krümmung ergibt sich aus dem Steigungswinkel
am Punkt der maximalen Krümmung ergibt sich aus dem Steigungswinkel ![]() zu
zu![]() . Für
. Für ![]() ist dieser Winkel
ist dieser Winkel ![]() . Mit wachsendem Exponenten wird der Winkel flacher und neigt sich schnell zu Werten über
. Mit wachsendem Exponenten wird der Winkel flacher und neigt sich schnell zu Werten über ![]() hin. Bei dem Exponenten
hin. Bei dem Exponenten ![]() ist der Normalenwinkel genau
ist der Normalenwinkel genau ![]() . In Abbildung 10 sind die Positionen der Punkte maximaler Krümmung
. In Abbildung 10 sind die Positionen der Punkte maximaler Krümmung ![]() (rote Kurve) zusammen mit den Mittelpunkten
(rote Kurve) zusammen mit den Mittelpunkten ![]() der entsprechenden Krümmungskreise (blaue Kurve) parametrisiert mit dem Exponenten
der entsprechenden Krümmungskreise (blaue Kurve) parametrisiert mit dem Exponenten ![]() aufgetragen. Für einige ausgewählte Parameter
aufgetragen. Für einige ausgewählte Parameter ![]() sind die Verbindungsstrecken
sind die Verbindungsstrecken ![]() gezeichnet (gestrichelte blaue Linien). Zusätzlich sind für
gezeichnet (gestrichelte blaue Linien). Zusätzlich sind für ![]() und
und ![]() die Winkel der Normalen auf der Kurve
die Winkel der Normalen auf der Kurve ![]() explizit dargestellt.
explizit dargestellt.
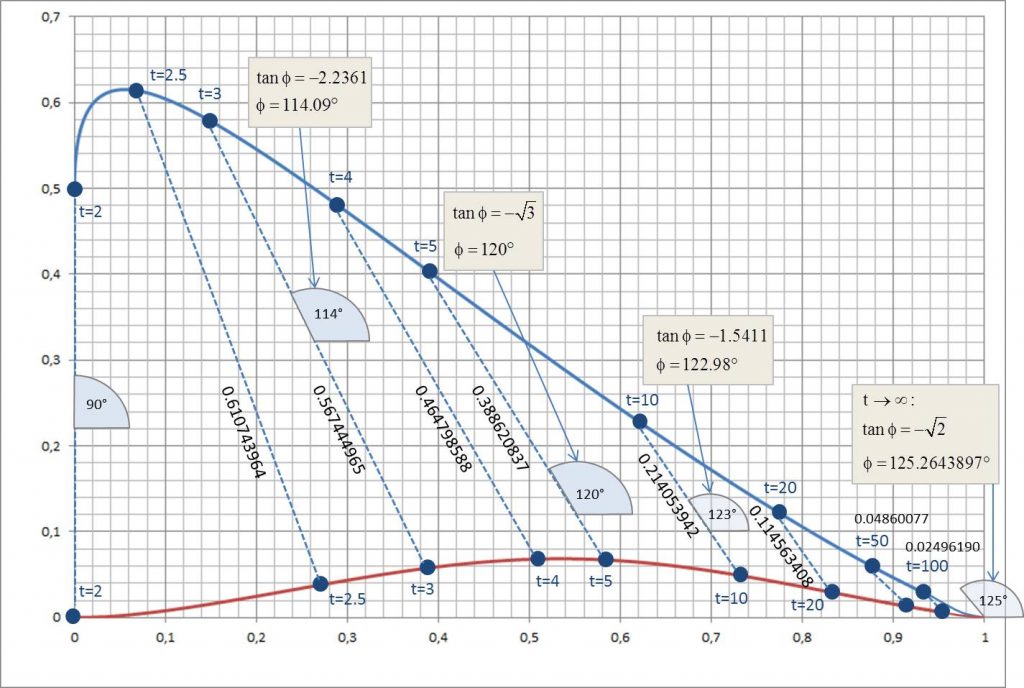
Abbildung 10
Formal folgt aus Formel (31)
(37) 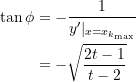
Damit erhält man für die Näherungsausdrücke wie oben
(38) 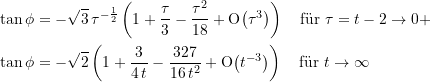
und somit auch den Grenzwert
(39) ![]()
In dem „unscheinbaren“ Winkel ![]() stecken gewissermaßen alle Informationen über die fraglichen Größen
stecken gewissermaßen alle Informationen über die fraglichen Größen ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() und
und ![]() : Aus
: Aus ![]() lassen sich alle anderen Werte berechnen, denn Formel (44) ist einfach nach
lassen sich alle anderen Werte berechnen, denn Formel (44) ist einfach nach ![]() auflösbar. Es gilt
auflösbar. Es gilt
(40) 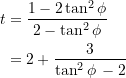
wobei ![]() im Bereich zwischen
im Bereich zwischen ![]() und
und ![]() liegt (das entspricht dem obigen Wert für
liegt (das entspricht dem obigen Wert für ![]() . – Hat man also den Winkel
. – Hat man also den Winkel ![]() und die Lage eines gegebenen Punkts
und die Lage eines gegebenen Punkts ![]() als Platzhalter für den Mittelpunkt des Krümmungskreises oder den Punkt maximaler Krümmung eines zunächst noch unbekannten Monoms, so können daraus die weiteren Größen und Positionen direkt berechnet werden.
als Platzhalter für den Mittelpunkt des Krümmungskreises oder den Punkt maximaler Krümmung eines zunächst noch unbekannten Monoms, so können daraus die weiteren Größen und Positionen direkt berechnet werden.
Wenn wir nun für ![]() die Approximationen für
die Approximationen für ![]() ,
, ![]() ,
, ![]() ,
, ![]() und
und ![]() im Zusammenhang betrachten, erkennen wir die folgenden Beziehungen
im Zusammenhang betrachten, erkennen wir die folgenden Beziehungen
(41) 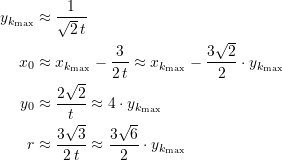
Wegen Formel (8) können wir das ergänzen um
(42) 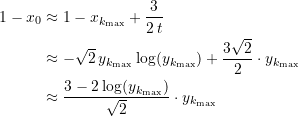
Der Abstand ![]() der Peripherie des Krümmungskreises von der
der Peripherie des Krümmungskreises von der ![]() -Achse ergibt sich somit zu
-Achse ergibt sich somit zu
(43) 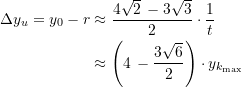
Analog folgt für Abstand ![]() der Peripherie des Krümmungskreises von der vertikalen Geraden bei
der Peripherie des Krümmungskreises von der vertikalen Geraden bei ![]()
(44) 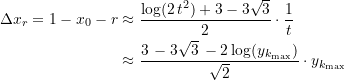
Insgesamt erhalten wir in der Situation ![]() in erster Näherung die in Abbildung 11 (Skizze A) dargestellte Konstellation. Ausgehend von der typischen Kurve für
in erster Näherung die in Abbildung 11 (Skizze A) dargestellte Konstellation. Ausgehend von der typischen Kurve für ![]() und der Position von
und der Position von ![]() auf der schematischen
auf der schematischen ![]() -Achse sind die davon abgeleiteten Werte für
-Achse sind die davon abgeleiteten Werte für ![]() ,
, ![]() und
und ![]() sowie die daraus resultierenden Positionen der betreffenden Punkte eingetragen. Der Wert von
sowie die daraus resultierenden Positionen der betreffenden Punkte eingetragen. Der Wert von ![]() ergibt sich als Ergebnis dieser Konstruktion. Wie groß wir
ergibt sich als Ergebnis dieser Konstruktion. Wie groß wir ![]() auch immer wählen, bleiben die Beziehungen zwischen den genannten Größen bis auf marginale, in der erreichbaren Genauigkeit einer Zeichnung gar nicht darstellbaren Änderungen völlig gleich. Der Parameter
auch immer wählen, bleiben die Beziehungen zwischen den genannten Größen bis auf marginale, in der erreichbaren Genauigkeit einer Zeichnung gar nicht darstellbaren Änderungen völlig gleich. Der Parameter ![]() spielt damit also die Rolle des Maßstabsfaktors.
spielt damit also die Rolle des Maßstabsfaktors.
Vorausgesetzt, wir betrachten weiter große ![]() , so können wir die Zusammenhänge sogar ohne jeden Bezug auf den Exponenten schon mit der Referenzgröße
, so können wir die Zusammenhänge sogar ohne jeden Bezug auf den Exponenten schon mit der Referenzgröße ![]() für
für ![]() asymptotisch korrekt darstellen (s. Abbildung 11, Skizze B).
asymptotisch korrekt darstellen (s. Abbildung 11, Skizze B).
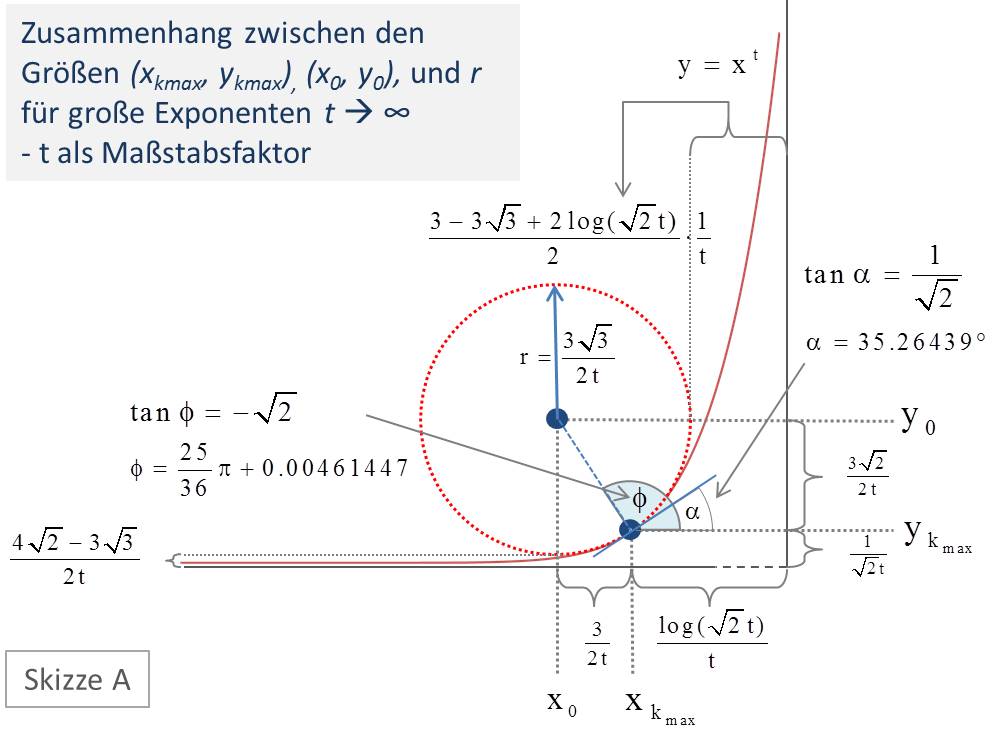
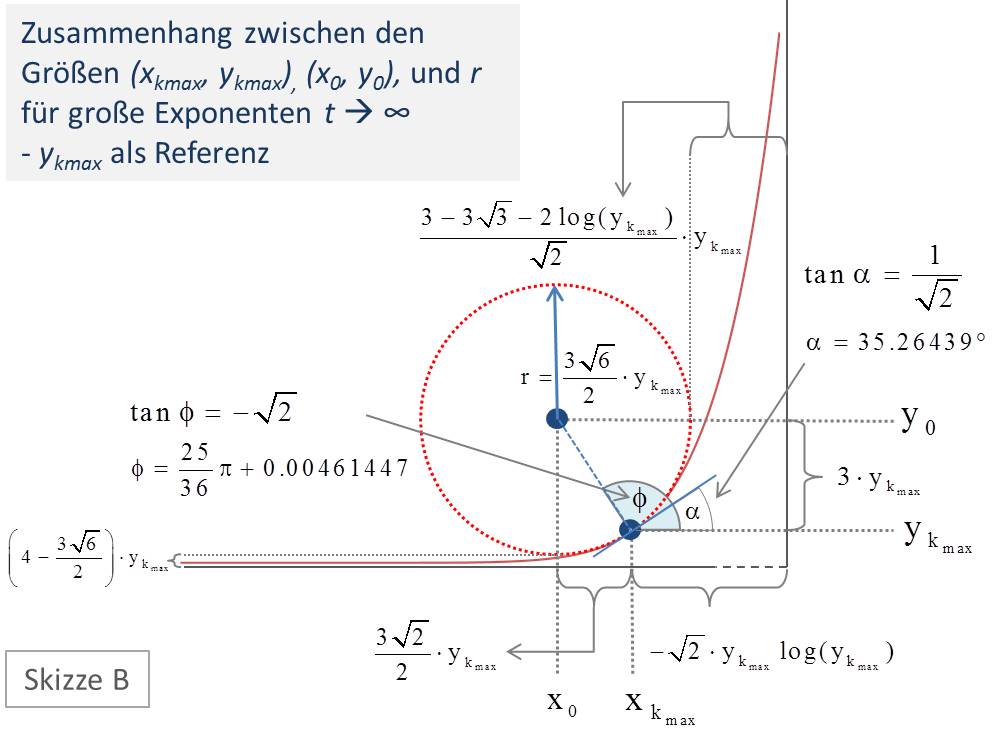
Abbildung 11a/b


