- Die Originalvariante
- Die Variante mit vier Schubladen und das Geschwisterproblem
- Das verallgemeinerte Paradoxon mit 3 Schubladen
- Das verallgemeinerte Paradoxon mit n Kästchen pro Schublade
- Abwandlung des verallgemeinerten Paradoxons
- Zusammenfassung zum verallgemeinerten Kästchenparadoxon
- Weitere Varianten
2 Das „Bertrand’sche Kästchenparadoxon“ 
2.1 Die Originalvariante
Das Paradoxon ist nach dem französischen Mathematiker Joseph Bertrand (1822-1900) benannt. Es gibt verschiedene Fassungen des Paradoxons mit teilweise unterschiedlichen Bezeichnungen. Wir orientieren uns in der folgenden Aufgabenformulierung an der Originalfassung:
- (1) Wir haben
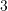 Schubladen mit jeweils zwei Kästchen:
Schubladen mit jeweils zwei Kästchen: - Die beiden Kästchen in Schublade
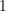 enthalten je eine Goldmünze.
enthalten je eine Goldmünze. - Die beiden Kästchen in Schublade
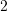 enthalten je eine Silbermünze.
enthalten je eine Silbermünze. - Eines der beiden Kästchen in Schublade
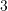 enthält eine Goldmünze, das andere eine Silbermünze.
enthält eine Goldmünze, das andere eine Silbermünze. - Man zieht eine Schublade, öffnet eines der beiden Kästchen und findet eine Goldmünze.
- Mit welcher Wahrscheinlichkeit befindet sich im anderen Kästchen eine Silbermünze?
Heute würde man die Aufgabe nicht mehr als Paradoxon bezeichnen. Diese Qualifizierung stammt aus einer Zeit, als man in der Mathematik noch keinen formal stimmigen Begriff von Wahrscheinlichkeitsverteilungen, bedingten Wahrscheinlichkeiten und Wahrscheinlichkeitsräumen entwickelt hatte.
Um das Ergebnis vorwegzunehmen: im anderen Kästchen befindet sich mit der Wahrscheinlichkeit ![]() eine Silbermünze.
eine Silbermünze.
Die Auswahlsituation können wir uns anhand des folgenden Schemas veranschaulichen:
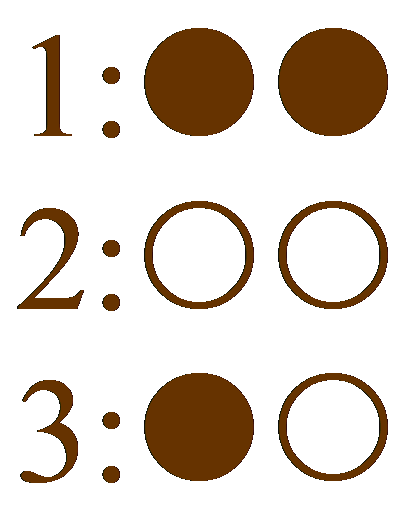
Das Symbol ![]() steht hier für ein Kästchen mit einer Goldmünze,
steht hier für ein Kästchen mit einer Goldmünze, ![]() meint ein Kästchen mit Silbermünze. Ohne Beschränkung der Allgemeinheit haben wir dabei die Goldmünze in Schublade 3 in das linke Kästchen gelegt.
meint ein Kästchen mit Silbermünze. Ohne Beschränkung der Allgemeinheit haben wir dabei die Goldmünze in Schublade 3 in das linke Kästchen gelegt.
Nehmen wir zur Beschreibung des Ereignisraums die folgende Notation:
![]()
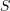 = gewählte Schublade
= gewählte Schublade
(1, 2 oder 3)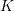 = gewähltes Kästchen
= gewähltes Kästchen
(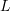 für links oder
für links oder 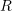 für rechts)
für rechts)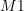 = gefundene Münze im gewählten Kästchen
= gefundene Münze im gewählten Kästchen
(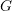 für Gold oder
für Gold oder 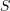 für Silber)
für Silber)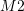 = Münze im anderen Kästchen
= Münze im anderen Kästchen
(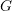 für Gold oder
für Gold oder 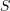 für Silber)
für Silber)
Der Ereignisraum wird nun durch die folgende Tabelle vollständig beschrieben:
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
Tabelle 2‑1
Wie man unmittelbar erkennt, erfüllen nur die Zeilen ![]() und
und ![]() von Tabelle 2‑1 die Voraussetzungen der Fragestellung (Man zieht eine Schublade, öffnet eines der beiden Kästchen und findet eine Goldmünze), weil nur in diesen drei Fällen eine Goldmünze gefunden werden kann. Diese drei Zeilen beschreiben die relevante Grundgesamtheit. Nur im Falle der Zeile
von Tabelle 2‑1 die Voraussetzungen der Fragestellung (Man zieht eine Schublade, öffnet eines der beiden Kästchen und findet eine Goldmünze), weil nur in diesen drei Fällen eine Goldmünze gefunden werden kann. Diese drei Zeilen beschreiben die relevante Grundgesamtheit. Nur im Falle der Zeile ![]() aber befindet sich im anderen Kästchen eine Silbermünze. Da die Auswahl von Schublade und Kästchen indessen gleichwahrscheinlich ist, ist daher die Wahrscheinlichkeit eine Silbermünze zu finden
aber befindet sich im anderen Kästchen eine Silbermünze. Da die Auswahl von Schublade und Kästchen indessen gleichwahrscheinlich ist, ist daher die Wahrscheinlichkeit eine Silbermünze zu finden ![]() .
.
Zum gleichen Ergebnis kommt man natürlich auch dann, wenn man die Problematik ganz formal angeht und konsequent absolute und bedingte Wahrscheinlichkeiten auseinander hält. Nehmen wir ![]() als das Ereignis, im ersten Schritt ein Kästchen mit einer Goldmünze zu wählen und S als das Ereignis, im zweiten gewählten Kästchen eine Silbermünze vorzufinden. Nur bei Ziehen einer der Schubladen
als das Ereignis, im ersten Schritt ein Kästchen mit einer Goldmünze zu wählen und S als das Ereignis, im zweiten gewählten Kästchen eine Silbermünze vorzufinden. Nur bei Ziehen einer der Schubladen ![]() oder
oder ![]() kann man überhaupt auf eine Goldmünze stoßen. Die Wahrscheinlichkeit für die Auswahl von Schublade
kann man überhaupt auf eine Goldmünze stoßen. Die Wahrscheinlichkeit für die Auswahl von Schublade ![]() oder
oder ![]() ist
ist ![]() . Da in Schublade 1 zwei Goldmünzen liegen, findet man schon im ersten Kästchen mit Sicherheit eine Goldmünze. Wurde dagegen Schublade
. Da in Schublade 1 zwei Goldmünzen liegen, findet man schon im ersten Kästchen mit Sicherheit eine Goldmünze. Wurde dagegen Schublade ![]() gewählt, so stehen die Chancen Halbe-Halbe, im zuerst gewählten Kästchen eine Goldmünze vorzufinden. Insgesamt ist demzufolge die (absolute) Wahrscheinlichkeit für das Eintreten von
gewählt, so stehen die Chancen Halbe-Halbe, im zuerst gewählten Kästchen eine Goldmünze vorzufinden. Insgesamt ist demzufolge die (absolute) Wahrscheinlichkeit für das Eintreten von ![]() gleich
gleich ![]() . Ist das Ereignis
. Ist das Ereignis ![]() aber in Schublade 3 eingetreten, so liegt im anderen Kästchen mit Sicherheit eine Silbermünze. Eine weitere Möglichkeit für das Eintreffen des Ereignisses
aber in Schublade 3 eingetreten, so liegt im anderen Kästchen mit Sicherheit eine Silbermünze. Eine weitere Möglichkeit für das Eintreffen des Ereignisses ![]() gibt es nicht (insbesondere nicht bei den beiden anderen Schubladen), daher ist die absolute Wahrscheinlichkeit, unter diesen Vorgaben eine Silbermünze zu finden (Ereignis
gibt es nicht (insbesondere nicht bei den beiden anderen Schubladen), daher ist die absolute Wahrscheinlichkeit, unter diesen Vorgaben eine Silbermünze zu finden (Ereignis ![]() ) gleich
) gleich ![]() . Daraus bestimmt sich nun die Wahrscheinlichkeit des bedingten Ereignisses
. Daraus bestimmt sich nun die Wahrscheinlichkeit des bedingten Ereignisses ![]() = „Kästchen mit Silbermünze wird geöffnet, nachdem zuvor eine Goldmünze gefunden wurde“ zu
= „Kästchen mit Silbermünze wird geöffnet, nachdem zuvor eine Goldmünze gefunden wurde“ zu ![]() .
.
Nimmt man Schublade ![]() aus der Problemstellung heraus, so müssen die obigen Zeilen
aus der Problemstellung heraus, so müssen die obigen Zeilen ![]() und
und ![]() aus dem Ereignisraum gestrichen werden. Dies ändert indessen nichts daran, dass dann auch weiterhin die relevante Grundgesamtheit durch die Ereignisse
aus dem Ereignisraum gestrichen werden. Dies ändert indessen nichts daran, dass dann auch weiterhin die relevante Grundgesamtheit durch die Ereignisse ![]() .
. ![]() und
und ![]() [Zeilen
[Zeilen ![]() und
und ![]() aus obiger Tabelle] gebildet wird. Daher ist auch in diesem Falle die Wahrscheinlichkeit eine Silbermünze zu finden
aus obiger Tabelle] gebildet wird. Daher ist auch in diesem Falle die Wahrscheinlichkeit eine Silbermünze zu finden ![]() .
.
Das gleiche gilt natürlich auch dann, wenn Schublade ![]() (Silber, Silber) mehrfach vorkommt, weil dadurch die relevante Grundgesamtheit nicht tangiert wird. Egal wie viele Schubladen mit zwei Silbermünzen existieren, die Wahrscheinlichkeit eine Silbermünze zu finden, wenn zuvor eine Goldmünze gefunden wurde, bleibt unverändert bei
(Silber, Silber) mehrfach vorkommt, weil dadurch die relevante Grundgesamtheit nicht tangiert wird. Egal wie viele Schubladen mit zwei Silbermünzen existieren, die Wahrscheinlichkeit eine Silbermünze zu finden, wenn zuvor eine Goldmünze gefunden wurde, bleibt unverändert bei ![]() .
.
Letztlich geht es auch beim „Bertrand’schen Kästchenparadoxon“ um die Bestimmung der Wahrscheinlichkeit eines bedingten Ereignisses. Das Hinzufügen oder Weglassen von Ereignissen, die den gestellten Bedingungen nicht entsprechen, ändert nun aber trivialerweise nichts am Ergebnis, deswegen ist die Wahrscheinlichkeit in jedem Falle ![]() .
.
2.2 Die Variante mit vier Schubladen und das Geschwisterproblem
Betrachten wir eine Variante zum Kästchenparadoxon.
- (2) Wir haben
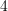 Schubladen mit jeweils zwei Kästchen:
Schubladen mit jeweils zwei Kästchen: - Die beiden Kästchen in Schublade
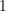 enthalten je eine Goldmünze.
enthalten je eine Goldmünze. - Die beiden Kästchen in Schublade
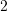 enthalten je eine Silbermünze.
enthalten je eine Silbermünze. - Schubladen
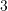 und
und 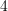 : in einem Kästchen befindet sich eine Goldmünze, in dem anderen eine Silbermünze.
: in einem Kästchen befindet sich eine Goldmünze, in dem anderen eine Silbermünze. - Man zieht eine Schublade, öffnet eines der beiden Kästchen und findet eine Goldmünze.
- Mit welcher Wahrscheinlichkeit befindet sich im anderen Kästchen eine Silbermünze?
Ohne Beschränkung der Allgemeinheit haben wir dabei die Goldmünze in Schublade ![]() in das linke, und in Schublade
in das linke, und in Schublade ![]() in das rechte Kästchen gelegt. Die Schubladenanordnung wird durch das folgende Schema verdeutlicht:
in das rechte Kästchen gelegt. Die Schubladenanordnung wird durch das folgende Schema verdeutlicht:
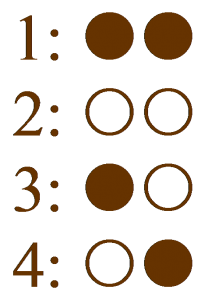
In obiger Notation haben wir nun den folgenden Ereignisraum:
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
Tabelle 2‑2
Wie man unmittelbar erkennt, erfüllen nun die Zeilen ![]() und
und ![]() von Tabelle 2‑2 die Voraussetzungen der Fragestellung (Man zieht eine Schublade, öffnet eines der beiden Kästchen und findet eine Goldmünze), weil nur in diesen vier Fällen eine Goldmünze gefunden werden kann. Die relevante Grundgesamtheit wird durch diese vier Zeilen beschrieben. Im Falle der Zeilen
von Tabelle 2‑2 die Voraussetzungen der Fragestellung (Man zieht eine Schublade, öffnet eines der beiden Kästchen und findet eine Goldmünze), weil nur in diesen vier Fällen eine Goldmünze gefunden werden kann. Die relevante Grundgesamtheit wird durch diese vier Zeilen beschrieben. Im Falle der Zeilen ![]() und
und ![]() befindet sich im anderen Kästchen eine Silbermünze. Aufgrund der zufälligen Auswahl von Schublade und Kästchen, ist daher die Wahrscheinlichkeit eine Silbermünze zu finden
befindet sich im anderen Kästchen eine Silbermünze. Aufgrund der zufälligen Auswahl von Schublade und Kästchen, ist daher die Wahrscheinlichkeit eine Silbermünze zu finden ![]() .
.
In der Argumentation mit bedingten Wahrscheinlichkeiten erhält man analog (mit den Bezeichnungen wie oben)
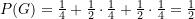
(Schublade 1 + ½*Schublade 3 + ½*Schublade 4)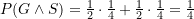
(½*Schublade 3 + ½*Schublade 4)
sowie
in Übereinstimmung mit der aus der Ereignistabelle abgeleiteten Lösung.
Bei Betrachtung des Schubladenschemas zu (2) sticht die Analogie zum Geschwisterproblem ins Auge. Scheinbar ist die Grundgesamtheit „irgendwie“ äquivalent zur Grundgesamtheit beim Geschwisterproblem. Hier kommen in den vier Schubladen alle Kombinationen (Gold, Gold) bis (Silber, Silber) vor, dort alle Paare ![]() bis
bis ![]() :
:
| 1 | |
| 2 | |
| 3 | |
| 4 |
Tabelle 2‑3
Doch wie sieht es mit der Entsprechung zum Geschwisterproblem tatsächlich aus? – Die Analogie ist bloßer Schein! Der Unterschied liegt im genauen Ablauf: im Auswahlprozess und der daraus resultierenden Sequenzierung der Teilereignisse im Kästchenparadoxon nach (2). Nach den Voraussetzungen im Geschwisterproblem ist bereits im Vorfeld (ohne irgendeine experimentelle Handlung) bekannt:
- Die Familie hat zwei Kinder. Dies entspricht den zwei Münzen pro Schublade.
- Eines der Kinder ist ein Mädchen. Mit der charmanten Definition Mädchen=Gold, Junge=Silber, bedeutet dies im übertragenen Sinne, dass nur Schubladen mit mindestens einer Goldmünze interessieren, in der Variante des Kästchenparadoxons also nur die Schubladen
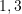 und
und 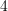 .
.
Soweit ist also noch Übereinstimmung gegeben. Nun kommt aber der entscheidende Gegensatz. Es geht weiter mit der Frage:
- Mit welcher Wahrscheinlichkeit ist auch das zweite Kind ein Mädchen?“ Beim Kästchenparadoxon heißt es dagegen: Man zieht eine Schublade, öffnet eines der beiden Kästchen und findet eine Goldmünze. Frage: mit welcher Wahrscheinlichkeit befindet sich im anderen Kästchen eine Silbermünze (bzw. eine Goldmünze um im Bild und in der Analogie zu bleiben)?
Zunächst weiß man in beiden Fällen nach Auswahl der Schublade, dass dieselbe ein Kästchen mit einer Goldmünze enthält. Dann aber geht es im nächsten Schritt beim Geschwisterproblem nur noch darum, ob auch das zweite Kästchen eine Goldmünze enthält. So kann man aber nur dann fragen, wenn „das eine Kästchen“ seinen Inhalt bereits preisgegeben hat, also schon offen ist. Mit anderen Worten, nach Ziehen der Schublade darf es nur noch ein verschlossenes Kästchen geben, will man den Rahmenbedingungen des Rätsels vollauf Rechnung tragen. Damit ist schon jetzt klar: Geschwisterproblem und Kästchenparadoxon sind zwei wesentlich verschiedene Problemstellungen. In Schublade ![]() enthält das verschlossene Kästchen eine Goldmünze, in den beiden anderen Schubladen (
enthält das verschlossene Kästchen eine Goldmünze, in den beiden anderen Schubladen (![]() und
und ![]() ) zwangsläufig je eine Silbermünze. Die Wahrscheinlichkeit, dass „das zweite Kästchen“ eine Goldmünze enthält, sprich, dass das zweite Kind ein Mädchen ist, ist daher gleich
) zwangsläufig je eine Silbermünze. Die Wahrscheinlichkeit, dass „das zweite Kästchen“ eine Goldmünze enthält, sprich, dass das zweite Kind ein Mädchen ist, ist daher gleich ![]() . Diese Übereinstimmung mit der obigen Behandlung des Geschwisterproblem erzielt man aber eben nur durch sinngemäße Anpassung des Ablaufs im Kästchenparadoxon.
. Diese Übereinstimmung mit der obigen Behandlung des Geschwisterproblem erzielt man aber eben nur durch sinngemäße Anpassung des Ablaufs im Kästchenparadoxon.
Beim Kästchenparadoxon weiß man nach dem Öffnen von Schublade ![]() oder
oder ![]() noch nichts darüber, welches der beiden darin vorgefundenen Kästchen eine Goldmünze enthält – doch das ist nicht der entscheidende Punkt. Ausschlaggebend für die Verschiedenheit von Kästchenparadoxon und Geschwisterproblem ist die Behandlung von Schublade
noch nichts darüber, welches der beiden darin vorgefundenen Kästchen eine Goldmünze enthält – doch das ist nicht der entscheidende Punkt. Ausschlaggebend für die Verschiedenheit von Kästchenparadoxon und Geschwisterproblem ist die Behandlung von Schublade ![]() : da in beiden Kästchen eine Goldmünze liegt, hat man hier zwei Möglichkeiten, mit der ersten Kästchenauswahl eine Goldmünze zu finden. Hieraus resultiert eine Verdopplung der Chancen für die Realisierung des Ereignisses „in beiden Kästchen liegt eine Goldmünze“. Die aus der vorgeschriebenen zeitlichen Abfolge sich ergebende gesonderte Zählung der Ereignisse „linkes Kästchen wird geöffnet, enthält Gold – rechtes Kästchen wird geöffnet, enthält Gold“ und „rechtes Kästchen wird geöffnet, enthält Gold – linkes Kästchen wird geöffnet, enthält Gold“ findet auf Seiten des Geschwisterproblems keine Entsprechung. Schließlich macht es keinen Unterschied, ob nun „Kind 1 und Kind 2“ oder „Kind 2 und Kind 1“ jeweils Mädchen sind. Durch die Sequenzierung der Teilereignisse „linkes Kästchen wird geöffnet …“, „rechtes Kästchen wird geöffnet …“ mit dem im Falle von Schublade 1 stets gleichen Ergebnis „beide Kästchen enthalten eine Goldmünze“ wird die Analogie zum Geschwisterproblem zerstört. Mathematisch gesprochen: es gibt keine bijektive, also umkehrbare, Abbildung vom Ereignisraum des Kästchenparadoxons auf den Ereignisraum des Geschwisterproblems. Mit anderen Worten, die Variante des „Bertrand’schen Kästchenparadoxons “ (mit zwei Schubladen Gold/Silber) ist nicht äquivalent mit dem ursprünglichen Geschwisterparadoxon (s. Das Geschwisterparadoxon (1)), weswegen das Ergebnis
: da in beiden Kästchen eine Goldmünze liegt, hat man hier zwei Möglichkeiten, mit der ersten Kästchenauswahl eine Goldmünze zu finden. Hieraus resultiert eine Verdopplung der Chancen für die Realisierung des Ereignisses „in beiden Kästchen liegt eine Goldmünze“. Die aus der vorgeschriebenen zeitlichen Abfolge sich ergebende gesonderte Zählung der Ereignisse „linkes Kästchen wird geöffnet, enthält Gold – rechtes Kästchen wird geöffnet, enthält Gold“ und „rechtes Kästchen wird geöffnet, enthält Gold – linkes Kästchen wird geöffnet, enthält Gold“ findet auf Seiten des Geschwisterproblems keine Entsprechung. Schließlich macht es keinen Unterschied, ob nun „Kind 1 und Kind 2“ oder „Kind 2 und Kind 1“ jeweils Mädchen sind. Durch die Sequenzierung der Teilereignisse „linkes Kästchen wird geöffnet …“, „rechtes Kästchen wird geöffnet …“ mit dem im Falle von Schublade 1 stets gleichen Ergebnis „beide Kästchen enthalten eine Goldmünze“ wird die Analogie zum Geschwisterproblem zerstört. Mathematisch gesprochen: es gibt keine bijektive, also umkehrbare, Abbildung vom Ereignisraum des Kästchenparadoxons auf den Ereignisraum des Geschwisterproblems. Mit anderen Worten, die Variante des „Bertrand’schen Kästchenparadoxons “ (mit zwei Schubladen Gold/Silber) ist nicht äquivalent mit dem ursprünglichen Geschwisterparadoxon (s. Das Geschwisterparadoxon (1)), weswegen das Ergebnis ![]() für die Wahrscheinlichkeit eine zweite Goldmünze vorzufinden, nicht auf das Geschwisterproblem übertragbar ist.
für die Wahrscheinlichkeit eine zweite Goldmünze vorzufinden, nicht auf das Geschwisterproblem übertragbar ist.
2.3 Das verallgemeinerte Paradoxon mit 3 Schubladen
Wir betrachten die folgende Verallgemeinerungen zum Bertrand’schen Kästchenparadoxon
- (3) Wir haben
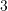 Schubladen mit jeweils
Schubladen mit jeweils 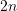 Kästchen:
Kästchen: - Die Schubladen tragen die Nummern
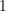 bis
bis 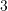 . In jeder Schublade befinden sich
. In jeder Schublade befinden sich 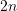 Kästchen, in jedem Kästchen liegt eine Gold- oder eine Silbermünze.
Kästchen, in jedem Kästchen liegt eine Gold- oder eine Silbermünze. - Schublade
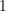 enthält nur Kästchen mit Goldmünzen.
enthält nur Kästchen mit Goldmünzen. - Schublade
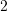 enthält genau
enthält genau 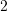 Kästchen mit einer Goldmünze sowie
Kästchen mit einer Goldmünze sowie 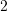 Kästchen mit Silbermünzen.
Kästchen mit Silbermünzen. - Schublade
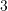 enthält nur Kästchen mit Silbermünzen.
enthält nur Kästchen mit Silbermünzen. - Man zieht zufällig eine Schublade, öffnet zufällig
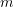 der Kästchen und findet jeweils eine Goldmünze (Ereignis
der Kästchen und findet jeweils eine Goldmünze (Ereignis 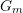 ).
). - Mit welcher Wahrscheinlichkeit befinden sich in den anderen Kästchen jeweils Silbermünzen (Ereignis
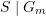 ) bzw. jeweils Goldmünzen (Ereignis
) bzw. jeweils Goldmünzen (Ereignis 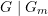 )?
)?
Setzen wir hier ![]() . so erhalten wir, abgesehen von den genauen Bezeichnungen und der Schubladenanordnung, die bereits oben diskutierte originale Form des Bertrand’schen Kästchenparadoxons (1).
. so erhalten wir, abgesehen von den genauen Bezeichnungen und der Schubladenanordnung, die bereits oben diskutierte originale Form des Bertrand’schen Kästchenparadoxons (1).
Zur Veranschaulichung mag das folgende Schema mit ![]() dienen (
dienen (![]() =Gold,
=Gold, ![]() =Silber):
=Silber):
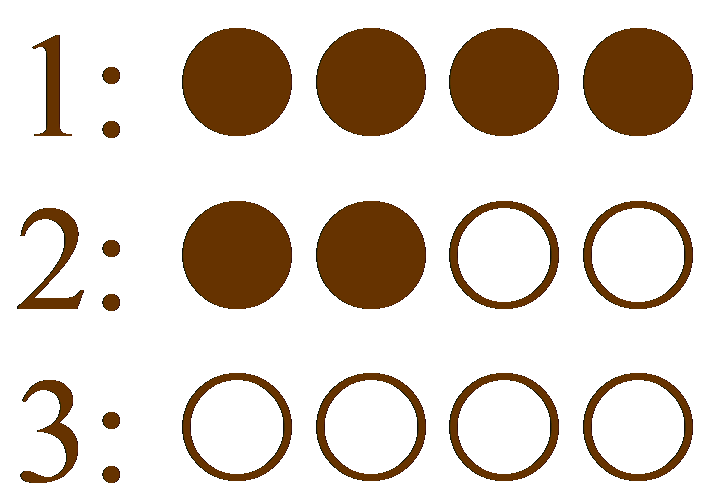
In Schublade ![]() gibt es
gibt es ![]() Möglichkeiten, unter den
Möglichkeiten, unter den ![]() Kästchen mit Goldmünzen genau
Kästchen mit Goldmünzen genau ![]() auszuwählen und zu öffnen. Dagegen sind es in Schublade
auszuwählen und zu öffnen. Dagegen sind es in Schublade ![]() genau
genau ![]() Fälle. Die Gesamtanzahl aller denkbaren Auswahlmöglichkeiten ist
Fälle. Die Gesamtanzahl aller denkbaren Auswahlmöglichkeiten ist ![]() . Wir erhalten demnach
. Wir erhalten demnach
(1) 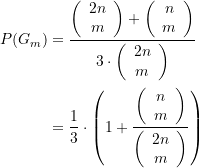
Speziell ist für ![]()
(2) ![]()
bzw. für ![]()
(3) ![]()
Speziell für ![]() gilt
gilt
(4) ![]()
Für ![]() geht also
geht also ![]() von
von ![]() auf wenig mehr als
auf wenig mehr als ![]() herunter. Und dies geht sehr schnell, denn für
herunter. Und dies geht sehr schnell, denn für ![]() lauten die ersten Werte von
lauten die ersten Werte von ![]() :
: ![]() bzw. von
bzw. von ![]() :
: ![]() . Daher wird der Quotient wie die Folge
. Daher wird der Quotient wie die Folge ![]() kleiner.
kleiner.
Nun zum Ereignis ![]() . Offensichtlich kann man nur in Schublade
. Offensichtlich kann man nur in Schublade ![]() nach dem Öffnen von
nach dem Öffnen von ![]() Kästchen mit Goldmünzen in den restlichen
Kästchen mit Goldmünzen in den restlichen ![]() Kästchen jeweils Silbermünzen vorfinden. Es gibt also unter allen denkbaren Auswahlmöglichkeiten für
Kästchen jeweils Silbermünzen vorfinden. Es gibt also unter allen denkbaren Auswahlmöglichkeiten für ![]() Goldmünzen nur eine einzige Realisierungschance für das fragliche Ereignis („ein Schublade wird gewählt, es werden
Goldmünzen nur eine einzige Realisierungschance für das fragliche Ereignis („ein Schublade wird gewählt, es werden ![]() Kästchen mit Goldmünzen gefunden, in den restlichen
Kästchen mit Goldmünzen gefunden, in den restlichen ![]() Kästchen befinden sich Silbermünzen“). Die Anzahl der Möglichkeiten zur Auswahl vom
Kästchen befinden sich Silbermünzen“). Die Anzahl der Möglichkeiten zur Auswahl vom ![]() Goldmünzen haben wir oben zu
Goldmünzen haben wir oben zu ![]() bestimmt. Insgesamt erhalten wir daher die fragliche Wahrscheinlichkeit
bestimmt. Insgesamt erhalten wir daher die fragliche Wahrscheinlichkeit ![]() zu.
zu.
(5) ![]()
Für ![]() sind dies die Wahrscheinlichkeiten
sind dies die Wahrscheinlichkeiten ![]() .
.
Die Wahrscheinlichkeit ![]() für
für ![]() Kästchen mit Goldmünzen, wenn zuvor bereits
Kästchen mit Goldmünzen, wenn zuvor bereits ![]() Kästchen mit Goldmünzen gewählt und geöffnet wurden ist ungleich höher, weil in Schublade 1 jede Auswahl zum Erfolg führt. Wir erhalten daher
Kästchen mit Goldmünzen gewählt und geöffnet wurden ist ungleich höher, weil in Schublade 1 jede Auswahl zum Erfolg führt. Wir erhalten daher
(6) 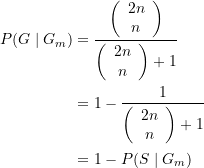
Setzen wir ![]() , so haben wir
, so haben wir ![]() sowie
sowie ![]() in Übereinstimmung mit der Originalversion des Paradoxons. Im oben skizzierten Schema mit 4 Kästchen pro Schublade ist
in Übereinstimmung mit der Originalversion des Paradoxons. Im oben skizzierten Schema mit 4 Kästchen pro Schublade ist ![]() . folglich ergibt sich
. folglich ergibt sich ![]() sowie
sowie ![]() .
.
2.4 Das verallgemeinerte Paradoxon mit n Kästchen pro Schublade
Im Folgenden betrachten wir weitere Verallgemeinerungen zum Bertrand’schen Kästchenparadoxon
- (4) Wir haben
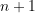 Schubladen mit jeweils
Schubladen mit jeweils  Kästchen:
Kästchen: - Die Schubladen tragen die Nummern
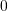 bis
bis  . In jeder Schublade befinden sich
. In jeder Schublade befinden sich  Kästchen, in jedem Kästchen liegt eine Gold- oder eine Silbermünze.
Kästchen, in jedem Kästchen liegt eine Gold- oder eine Silbermünze. - Schublade
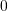 enthält nur Kästchen mit Silbermünzen.
enthält nur Kästchen mit Silbermünzen. - Schublade
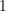 enthält genau
enthält genau 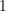 Kästchen mit einer Goldmünze und
Kästchen mit einer Goldmünze und  Kästchen mit Silbermünzen.
Kästchen mit Silbermünzen. - Schublade
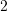 enthält genau
enthält genau 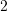 Kästchen mit einer Goldmünze und
Kästchen mit einer Goldmünze und  Kästchen mit Silbermünzen.
Kästchen mit Silbermünzen. - Und so weiter, bis Schublade
 . in der sich genau
. in der sich genau  Kästchen mit einer Goldmünze (und keine Kästchen mit Silbermünzen) befinden.
Kästchen mit einer Goldmünze (und keine Kästchen mit Silbermünzen) befinden. - Man zieht zufällig eine Schublade, öffnet zufällig m der Kästchen und findet jeweils eine Goldmünze (Ereignis
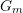 ).
). - Mit welcher Wahrscheinlichkeit befinden sich in den anderen Kästchen jeweils Silbermünzen (Ereignis
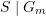 ) bzw. jeweils Goldmünzen (Ereignis
) bzw. jeweils Goldmünzen (Ereignis 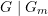 )?
)?
Setzen wir hier ![]() . so erhalten wir, abgesehen von den genauen Bezeichnungen und der Schubladenanordnung, die bereits oben diskutierte originale Form des Bertrand’schen Kästchenparadoxons (1).
. so erhalten wir, abgesehen von den genauen Bezeichnungen und der Schubladenanordnung, die bereits oben diskutierte originale Form des Bertrand’schen Kästchenparadoxons (1).
Zur Veranschaulichung mag das folgende Schema dienen (![]() =Gold,
=Gold, ![]() =Silber):
=Silber):
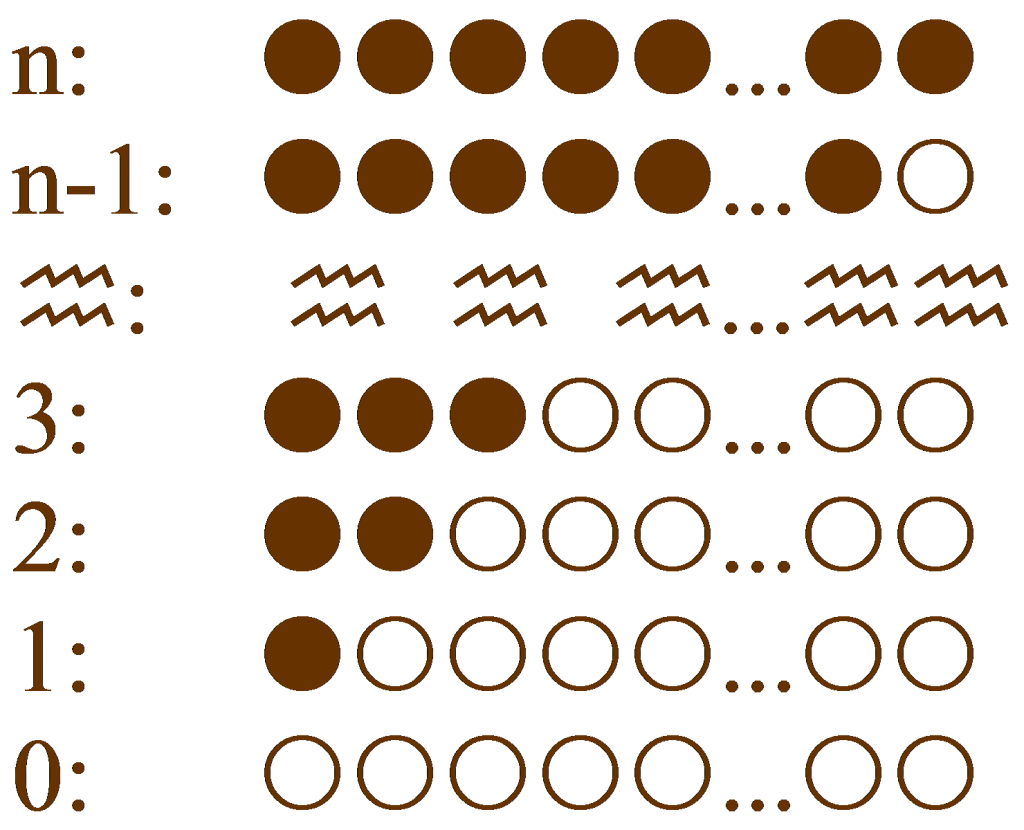
Man mache sich klar, dass hier nicht gefragt wird, mit welcher Wahrscheinlichkeit ![]() das Ereignis „es werden
das Ereignis „es werden ![]() Kästchen mit Goldmünzen gefunden“ überhaupt eintritt. Dieses Ereignis wird in der Problemstellung vielmehr als bereits eingetreten vorausgesetzt. Im Sinne einer Vorbereitung betrachten wir zunächst dennoch die einfachere Fragestellung nach der Chance, unter den
Kästchen mit Goldmünzen gefunden“ überhaupt eintritt. Dieses Ereignis wird in der Problemstellung vielmehr als bereits eingetreten vorausgesetzt. Im Sinne einer Vorbereitung betrachten wir zunächst dennoch die einfachere Fragestellung nach der Chance, unter den ![]() Schubladen nach zufälliger Auswahl einer Schublade
Schubladen nach zufälliger Auswahl einer Schublade ![]() Kästchen mit Goldmünzen zu finden.
Kästchen mit Goldmünzen zu finden.
Offensichtlich enthalten nur die Schubladen ![]() bis
bis ![]() mindestens
mindestens ![]() Goldmünzen. Hat man eine dieser Schubladen gewählt, sagen wie die Schublade
Goldmünzen. Hat man eine dieser Schubladen gewählt, sagen wie die Schublade ![]() . wobei
. wobei ![]() die Werte null bis
die Werte null bis ![]() annehmen kann, so gibt es
annehmen kann, so gibt es ![]() Möglichkeiten, unter den
Möglichkeiten, unter den ![]() Kästchen mit Goldmünzen genau
Kästchen mit Goldmünzen genau ![]() auszuwählen und zu öffnen. Über alle Schubladen mit mindestens
auszuwählen und zu öffnen. Über alle Schubladen mit mindestens ![]() Goldmünzen summiert, beläuft sich die Anzahl dieser Möglichkeiten daher auf
Goldmünzen summiert, beläuft sich die Anzahl dieser Möglichkeiten daher auf
(7) ![]()
Wir erhalten ![]() . wenn wir diese Anzahl zur Gesamtanzahl der denkbaren Fälle in Beziehung setzen. In jeder Schublade haben wir
. wenn wir diese Anzahl zur Gesamtanzahl der denkbaren Fälle in Beziehung setzen. In jeder Schublade haben wir ![]() Möglichkeiten, m Kästchen auszuwählen. Über alle n+1 Schubladen gerechnet ist demzufolge die Gesamtanzahl der denkbaren Fälle
Möglichkeiten, m Kästchen auszuwählen. Über alle n+1 Schubladen gerechnet ist demzufolge die Gesamtanzahl der denkbaren Fälle ![]() . Damit bekommen wir
. Damit bekommen wir
(8) 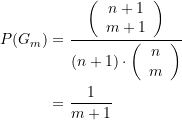
Die Wahrscheinlichkeit zum Auffinden von ![]() Kästchen mit Goldmünzen ist demzufolge unabhängig von der Anzahl der Münzen pro Schublade bzw. der Schubladenanzahl (natürlich vorausgesetzt, es befinden sich in jeder Schublade mindestens
Kästchen mit Goldmünzen ist demzufolge unabhängig von der Anzahl der Münzen pro Schublade bzw. der Schubladenanzahl (natürlich vorausgesetzt, es befinden sich in jeder Schublade mindestens ![]() Münzen). Das konnte man nicht unbedingt so erwarten, bedeutet es doch, dass in der folgenden Konstellation mit
Münzen). Das konnte man nicht unbedingt so erwarten, bedeutet es doch, dass in der folgenden Konstellation mit ![]() Münzen pro Schublade
Münzen pro Schublade
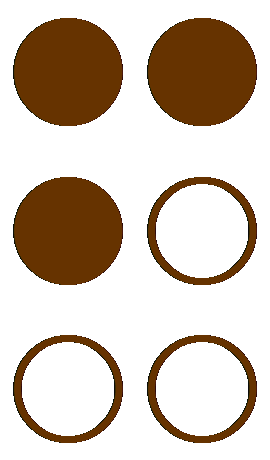
(![]() =Gold,
=Gold, ![]() =Silber) genau wie in der Situation mit, sagen wir
=Silber) genau wie in der Situation mit, sagen wir ![]() Münzen,
Münzen,

die Chance, nach Auswahl einer Schublade und von zwei Kästchen, dort auf Goldmünzen zu treffen gleich ![]() ist. Logischerweise ist die Wahrscheinlichkeit, stattdessen zwei Silbermünzen zu finden ebenfalls
ist. Logischerweise ist die Wahrscheinlichkeit, stattdessen zwei Silbermünzen zu finden ebenfalls ![]() . Für die gemischten Kombinationen Gold-Silber oder Silber-Gold ergibt sich demnach die Chance genauso zu
. Für die gemischten Kombinationen Gold-Silber oder Silber-Gold ergibt sich demnach die Chance genauso zu ![]() . Man könnte demnach sogar in Unkenntnis der Anzahl der Schubladen bzw. Münzen (
. Man könnte demnach sogar in Unkenntnis der Anzahl der Schubladen bzw. Münzen (![]() ) pro Schublade mit
) pro Schublade mit ![]() Erfolgschance darauf wetten, dass sich nach diesem Auswahlmodus in zwei zufällig gewählten Kästchen einer Schublade gleichartige Münzen befinden.
Erfolgschance darauf wetten, dass sich nach diesem Auswahlmodus in zwei zufällig gewählten Kästchen einer Schublade gleichartige Münzen befinden.
Die Unabhängigkeit der Wahrscheinlichkeit von der Anzahl der Münzen pro Schublade hängt zusammen mit der speziellen Gesamtanordnung. Würde man bei gleicher Gesamtmünzenanzahl und gleichem Verhältnis von Gold- und Silbermünzen die Münzen blind aus einer Urne herausgreifen (bzw. in eine Schublade legen und dort auswählen), so wäre die Chance für das Auffinden von ![]() Goldmünzen sehr wohl von der Anzahl der Münzen anhängig. Schauen wir z. B. auf die folgende Anordnung mit
Goldmünzen sehr wohl von der Anzahl der Münzen anhängig. Schauen wir z. B. auf die folgende Anordnung mit ![]() Münzen:
Münzen:
![]()
Wir haben hier die gleiche Anzahl Gold- und Silbermünzen wie im ursprünglichen Kästchenparadoxon. Die Wahrscheinlichkeit, bei zufälliger Wahl von zwei Kästchen dort auf Goldmünzen zu stoßen ist aber nicht ![]() (wie oben), sondern
(wie oben), sondern 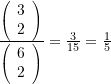 . Zudem verändert sich diese Wahrscheinlichkeit mit der Gesamtanzahl der Münzen. Für 30 Münzen (15 Gold- und 15 Silbermünzen) ergibt sich z. B. ein Wert von
. Zudem verändert sich diese Wahrscheinlichkeit mit der Gesamtanzahl der Münzen. Für 30 Münzen (15 Gold- und 15 Silbermünzen) ergibt sich z. B. ein Wert von 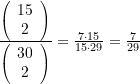 .
.
Wenden wir uns nun der eigentlichen Fragestellung nach der Wahrscheinlichkeit der Ereignisse ![]() und
und ![]() zu. Offensichtlich kann man überhaupt nur in Schublade
zu. Offensichtlich kann man überhaupt nur in Schublade ![]() nach dem Öffnen von
nach dem Öffnen von ![]() Kästchen mit Goldmünzen in den restlichen
Kästchen mit Goldmünzen in den restlichen ![]() Kästchen jeweils Silbermünzen vorfinden. Es gibt also unter allen denkbaren Auswahlmöglichkeiten nur eine einzige Realisierungschance für das fragliche Ereignis („ein Schublade wird gewählt, es werden
Kästchen jeweils Silbermünzen vorfinden. Es gibt also unter allen denkbaren Auswahlmöglichkeiten nur eine einzige Realisierungschance für das fragliche Ereignis („ein Schublade wird gewählt, es werden ![]() Kästchen mit Goldmünzen gefunden, in den restlichen
Kästchen mit Goldmünzen gefunden, in den restlichen ![]() Kästchen befinden sich Silbermünzen“). Die Anzahl der Möglichkeiten zur Auswahl vom
Kästchen befinden sich Silbermünzen“). Die Anzahl der Möglichkeiten zur Auswahl vom ![]() Goldmünzen haben wir oben zu
Goldmünzen haben wir oben zu ![]() bestimmt. Insgesamt erhalten wir daher die fragliche Wahrscheinlichkeit zu
bestimmt. Insgesamt erhalten wir daher die fragliche Wahrscheinlichkeit zu
(9) 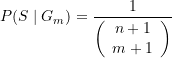
Zu beachten ist, dass es sich hier um eine bedingte Wahrscheinlichkeit handelt: es ist die Wahrscheinlichkeit dafür, „in den restlichen ![]() Kästchen Silbermünzen zu finden“, wenn in derselben Schublade zuvor „
Kästchen Silbermünzen zu finden“, wenn in derselben Schublade zuvor „![]() Kästchen mit Goldmünzen geöffnet worden waren“.
Kästchen mit Goldmünzen geöffnet worden waren“.
Im obigen Spezialfall mit drei Schubladen (also ![]() und
und ![]() ) ergibt sich
) ergibt sich
(10) 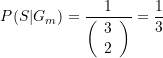
in Übereinstimmung mit dem bereits früher erhaltenen Resultat.
Wegen ![]() ist die Wahrscheinlichkeit unabhängig davon, ob wir das Ereignis betrachten, zuerst
ist die Wahrscheinlichkeit unabhängig davon, ob wir das Ereignis betrachten, zuerst ![]() Kästchen mit Goldmünzen zu öffnen und in den verbleibenden
Kästchen mit Goldmünzen zu öffnen und in den verbleibenden ![]() Kästchen stets Silbermünzen zu finden, oder ob wir stattdessen nach
Kästchen stets Silbermünzen zu finden, oder ob wir stattdessen nach ![]() Kästchen mit Goldmünzen und
Kästchen mit Goldmünzen und ![]() Silbermünzen fragen.
Silbermünzen fragen.
Betrachten wir als Beispiel eine Anordnung von ![]() Schubladen mit null bis
Schubladen mit null bis ![]() Goldmünzen und fragen wir nach der Wahrscheinlichkeit, nach Schubladenwahl und dem Öffnen von
Goldmünzen und fragen wir nach der Wahrscheinlichkeit, nach Schubladenwahl und dem Öffnen von ![]() Kästchen mit Goldmünzen im neunten Kästchen eine Silbermünze vorzufinden. Hier ist
Kästchen mit Goldmünzen im neunten Kästchen eine Silbermünze vorzufinden. Hier ist ![]() und
und ![]() . Damit erhalten wir
. Damit erhalten wir
(11) 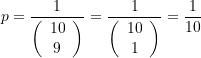
Das Resultat konnte man auch intuitiv so erwarten, schließlich gibt es ![]() Schubladen, und nur in genau einer davon befinden sich
Schubladen, und nur in genau einer davon befinden sich ![]() Kästchen mit einer Goldmünze sowie ein Kästchen mit einer Silbermünze. Keine Überraschung also. Doch ist diese Begründung überhaupt zutreffend? – Absolut gar nicht! Denn denken wir uns im vorliegenden Falle die Schubladen mit weniger als
Kästchen mit einer Goldmünze sowie ein Kästchen mit einer Silbermünze. Keine Überraschung also. Doch ist diese Begründung überhaupt zutreffend? – Absolut gar nicht! Denn denken wir uns im vorliegenden Falle die Schubladen mit weniger als ![]() Goldmünzen weg (das sind die
Goldmünzen weg (das sind die ![]() Schubladen
Schubladen ![]() bis
bis ![]() ), so verbleiben nur 2 Schubladen, die mit
), so verbleiben nur 2 Schubladen, die mit ![]() und die mit
und die mit ![]() Goldmünzen. Nur in diesen beiden Schubladen können wir tatsächlich 8 Kästchen mit Goldmünzen öffnen. Die acht anderen Schubladen gehen daher nicht in die Bestimmung der Wahrscheinlichkeit ein. Da nun also nur in einer der beiden überhaupt interessierenden Schubladen ein Kästchen mit Silbermünze existiert, könnte man intuitiv eher das Resultat
Goldmünzen. Nur in diesen beiden Schubladen können wir tatsächlich 8 Kästchen mit Goldmünzen öffnen. Die acht anderen Schubladen gehen daher nicht in die Bestimmung der Wahrscheinlichkeit ein. Da nun also nur in einer der beiden überhaupt interessierenden Schubladen ein Kästchen mit Silbermünze existiert, könnte man intuitiv eher das Resultat ![]() erwarten. Das richtige Ergebnis
erwarten. Das richtige Ergebnis ![]() kommt natürlich dadurch zustande, dass es in Schubladen
kommt natürlich dadurch zustande, dass es in Schubladen ![]() (mit
(mit ![]() Goldmünzen) eine, in Schublade
Goldmünzen) eine, in Schublade ![]() (mit
(mit ![]() Goldmünzen) aber genau neun Möglichkeiten gibt, darin
Goldmünzen) aber genau neun Möglichkeiten gibt, darin ![]() Gold-Kästchen auszuwählen.
Gold-Kästchen auszuwählen.
Ebenfalls ![]() ist nach obiger Symmetriebedingung die Wahrscheinlichkeit, direkt nach Auswahl einer Schublade
ist nach obiger Symmetriebedingung die Wahrscheinlichkeit, direkt nach Auswahl einer Schublade ![]() Silbermünzen vorzufinden. Dies leuchtet unmittelbar ein, weil genau eine der zehn Schubladen keine Goldmünze aber exakt
Silbermünzen vorzufinden. Dies leuchtet unmittelbar ein, weil genau eine der zehn Schubladen keine Goldmünze aber exakt ![]() Silbermünzen enthält. In diesem Falle ist die intuitive Vorstellung zutreffend, denn nun ist die Auswahl einer Schublade stets ein zählbares Ereignis, entweder positiv oder negativ. In der Tat kann wird man „keine Goldmünze“ finden, insbesondere dann, wenn man zunächst „kein Kästchen“ öffnet. Das ist natürlich immer möglich, und zwar in jeder Schublade exakt einmal. Aus diesem Grunde sind jetzt alle zehn Schubladen für den Ereignisraum relevant und müssen dabei genau einmal gezählt werden.
Silbermünzen enthält. In diesem Falle ist die intuitive Vorstellung zutreffend, denn nun ist die Auswahl einer Schublade stets ein zählbares Ereignis, entweder positiv oder negativ. In der Tat kann wird man „keine Goldmünze“ finden, insbesondere dann, wenn man zunächst „kein Kästchen“ öffnet. Das ist natürlich immer möglich, und zwar in jeder Schublade exakt einmal. Aus diesem Grunde sind jetzt alle zehn Schubladen für den Ereignisraum relevant und müssen dabei genau einmal gezählt werden.
Wenn in obiger Situation verlangt wird, zunächst ![]() Kästchen mit Goldmünzen zu öffnen, so ist die Wahrscheinlichkeit, danach auf
Kästchen mit Goldmünzen zu öffnen, so ist die Wahrscheinlichkeit, danach auf ![]() Kästchen mit Silbermünzen zu treffen
Kästchen mit Silbermünzen zu treffen
(12) 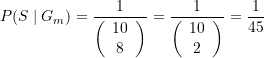
Zugleich ist dies die Chance, nach Auswahl von einem Gold-Kästchen anschließend auf ![]() Kästchen mit silbernem Inhalt zu stoßen. Es verwundert, dass diese Wahrscheinlichkeit gegenüber der Situation bei der Auswahl von neun Silbermünzen so niedrig ist. Indessen erklärt sich dies aus der Vielzahl der Möglichkeiten, nach Auswahl einer Schublade zunächst ein Kästchen mit goldenem Inhalt zu öffnen. Es sind dies insgesamt
Kästchen mit silbernem Inhalt zu stoßen. Es verwundert, dass diese Wahrscheinlichkeit gegenüber der Situation bei der Auswahl von neun Silbermünzen so niedrig ist. Indessen erklärt sich dies aus der Vielzahl der Möglichkeiten, nach Auswahl einer Schublade zunächst ein Kästchen mit goldenem Inhalt zu öffnen. Es sind dies insgesamt ![]() Fälle in den Schubladen
Fälle in den Schubladen ![]() bis
bis ![]() . Nur einmal aber enthalten die acht anderen Kästchen Silbermünzen. Ohne die Vorbedingung, ein Goldkästchen geöffnet zu haben, gibt es dagegen nur einmal pro Schublade (also insgesamt zehnmal) die Gelegenheit, überhaupt mit dem Öffnen von Silberkästchen zu beginnen. Die Chance, sodann gleich auf neun Kästchen mit Silbermünzen zu stoßen ist daher um den Faktor
. Nur einmal aber enthalten die acht anderen Kästchen Silbermünzen. Ohne die Vorbedingung, ein Goldkästchen geöffnet zu haben, gibt es dagegen nur einmal pro Schublade (also insgesamt zehnmal) die Gelegenheit, überhaupt mit dem Öffnen von Silberkästchen zu beginnen. Die Chance, sodann gleich auf neun Kästchen mit Silbermünzen zu stoßen ist daher um den Faktor ![]() größer.
größer.
Betrachten wir als weiteres Zahlenbeispiel die Chance 5 Silbermünzen zu finden, nachdem zuvor 4 Kästchen mit Goldmünzen geöffnet wurden. Nun ist ![]() . Wir erhalten
. Wir erhalten
(13) 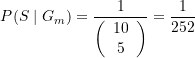
Das ist nun schon ein ziemlich unwahrscheinliches Ereignis. Dieser niedrige Wahrscheinlichkeitswert erstaunt. Offenkundig ist es weitaus wahrscheinlicher neun Silbermünzen zu finden ![]() . als
. als ![]() Gold- und
Gold- und ![]() Silbermünzen zu erhalten
Silbermünzen zu erhalten ![]() . obwohl doch in beiden Fällen genau neun Kästchen geöffnet werden müssen. Der Grund liegt natürlich auch hier in dem vorgeschriebenen Auswahlprozess. Die Kästchen werden ja sukzessive geöffnet und im letzteren Falle gibt es sehr viel mehr Möglichkeiten, zunächst vier Goldmünzen zu finden. Und nur in einem dieser Fälle enthalten die fünf verbleibenden Kästchen tatsächlich Silbermünzen.
. obwohl doch in beiden Fällen genau neun Kästchen geöffnet werden müssen. Der Grund liegt natürlich auch hier in dem vorgeschriebenen Auswahlprozess. Die Kästchen werden ja sukzessive geöffnet und im letzteren Falle gibt es sehr viel mehr Möglichkeiten, zunächst vier Goldmünzen zu finden. Und nur in einem dieser Fälle enthalten die fünf verbleibenden Kästchen tatsächlich Silbermünzen.
Die nachfolgende Tabelle 2‑4 gibt für alle ![]() von
von ![]() bis
bis ![]() und
und ![]() von
von ![]() bis
bis ![]() einen Überblick zur Wahrscheinlichkeit, nach Auswahl einer Schublade und von
einen Überblick zur Wahrscheinlichkeit, nach Auswahl einer Schublade und von ![]() Kästchen mit Goldmünzen auf
Kästchen mit Goldmünzen auf ![]() Kästchen mit Silbermünzen zu stoßen.
Kästchen mit Silbermünzen zu stoßen.
| Anzahl | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Anzahl | 1 | 1/2 | |||||||||
| 2 | 1/3 | 1/3 | |||||||||
| 3 | 1/4 | 1/6 | 1/4 | ||||||||
| 4 | 1/5 | 1/10 | 1/10 | 1/5 | |||||||
| 5 | 1/6 | 1/15 | 1/20 | 1/15 | 1/6 | ||||||
| 6 | 1/7 | 1/21 | 1/35 | 1/35 | 1/21 | 1/7 | |||||
| 7 | 1/8 | 1/28 | 1/56 | 1/70 | 1/56 | 1/28 | 1/8 | ||||
| 8 | 1/9 | 1/36 | 1/84 | 1/126 | 1/126 | 1/84 | 1/36 | 1/9 | |||
| 9 | 1/10 | 1/45 | 1/120 | 1/210 | 1/252 | 1/210 | 1/120 | 1/45 | 1/10 | ||
| 10 | 1/11 | 1/55 | 1/165 | 1/330 | 1/462 | 1/462 | 1/330 | 1/165 | 1/55 | 1/11 |
Tabelle 2‑4
Es ist nicht uninteressant, kontrastierend zur vorstehenden Untersuchung gezielt die Frage zu behandeln, mit welcher Wahrscheinlichkeit nach dem Öffnen von ![]() Kästchen mit Goldmünzen auch in den verbleibenden
Kästchen mit Goldmünzen auch in den verbleibenden ![]() Kästchen stets Goldmünzen zu finden sind (Ereignis
Kästchen stets Goldmünzen zu finden sind (Ereignis ![]() ). Auf den ersten Blick ist man geneigt, dieses Problem für vollkommen analog zu der oben behandelten Frage nach
). Auf den ersten Blick ist man geneigt, dieses Problem für vollkommen analog zu der oben behandelten Frage nach ![]() Silbermünzen abzutun. Denn
Silbermünzen abzutun. Denn ![]() Goldmünzen existieren ebenso wie
Goldmünzen existieren ebenso wie ![]() Silbermünzen nur in einer einzigen Schublade. Verschieden ist lediglich die Nummer der Schublade, einmal ist es die Nummer
Silbermünzen nur in einer einzigen Schublade. Verschieden ist lediglich die Nummer der Schublade, einmal ist es die Nummer ![]() . das andere Mal die Nummer
. das andere Mal die Nummer ![]() . Doch dieser erste unreflektierte Anschein trügt. Beim genaueren Hinschauen sieht man nämlich, dass in Schublade
. Doch dieser erste unreflektierte Anschein trügt. Beim genaueren Hinschauen sieht man nämlich, dass in Schublade ![]() genau
genau ![]() Möglichkeiten bestehen,
Möglichkeiten bestehen, ![]() Kästchen mit Goldmünzen zu öffnen. In jedem dieser Fälle befinden sich aber in den verbleibenden
Kästchen mit Goldmünzen zu öffnen. In jedem dieser Fälle befinden sich aber in den verbleibenden ![]() Kästchen ebenfalls Goldmünzen. Deshalb ist die fragliche Wahrscheinlichkeit
Kästchen ebenfalls Goldmünzen. Deshalb ist die fragliche Wahrscheinlichkeit ![]() für
für ![]() Kästchen mit Goldmünzen, wenn zuvor bereits
Kästchen mit Goldmünzen, wenn zuvor bereits ![]() Kästchen mit Goldmünzen gewählt und geöffnet wurden
Kästchen mit Goldmünzen gewählt und geöffnet wurden
(14) 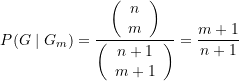
Überraschenderweise ist also die Chance, nach dem Öffnen von ![]() Kästchen mit Goldmünzen in den restlichen
Kästchen mit Goldmünzen in den restlichen ![]() Kästchen gleichfalls Goldmünzen vorzufinden – abgesehen vom Fall
Kästchen gleichfalls Goldmünzen vorzufinden – abgesehen vom Fall ![]() – stets größer, als die Wahrscheinlichkeit, stattdessen auf
– stets größer, als die Wahrscheinlichkeit, stattdessen auf ![]() Kästchen mit Silbermünzen zu stoßen. Teilweise macht der Unterschied ein Vielfaches aus.
Kästchen mit Silbermünzen zu stoßen. Teilweise macht der Unterschied ein Vielfaches aus.
Man kann die Formel auch so interpretieren: je mehr Goldmünzen man bereits gefunden hat (großes ![]() ), desto größer ist die Chance, in den restlichen Kästchen gleichfalls Goldmünzen zu entdecken. Mit anderen Worten, aus Reichtum wird mit einiger Wahrscheinlichkeit Überfluss. Oder, je klüger man ist, desto einfacher fällt es, sein Wissen zu vermehren (Zwei nicht ganz ernst gemeinte Hinweise, die indessen durch Lebenserfahrung belegt werden).
), desto größer ist die Chance, in den restlichen Kästchen gleichfalls Goldmünzen zu entdecken. Mit anderen Worten, aus Reichtum wird mit einiger Wahrscheinlichkeit Überfluss. Oder, je klüger man ist, desto einfacher fällt es, sein Wissen zu vermehren (Zwei nicht ganz ernst gemeinte Hinweise, die indessen durch Lebenserfahrung belegt werden).
Die folgende Tabelle 2‑5 gibt einen Überblick zu den aus der Formel erhaltenen Ergebnissen. Man entnimmt der Tabelle z. B. diese Aussagen (zum Vergleich s. a. Tabelle 2‑4):
Hat man in einer Anordnung von drei Schubladen mit je ![]() Münzen nach Auswahlvorschrift eine Goldmünze gefunden, so enthält das daraufhin geöffnete Kästchen der gleichen Schublade mit der Chance
Münzen nach Auswahlvorschrift eine Goldmünze gefunden, so enthält das daraufhin geöffnete Kästchen der gleichen Schublade mit der Chance ![]() ebenfalls eine Goldmünze (Anmerkung: hierbei handelt es sich um das ursprüngliche Kästchenparadoxon).
ebenfalls eine Goldmünze (Anmerkung: hierbei handelt es sich um das ursprüngliche Kästchenparadoxon).
Wurden in einer Schubladenanordnung von ![]() Münzen je Schublade zunächst
Münzen je Schublade zunächst ![]() Kästchen mit Goldmünzen geöffnet, so enthält auch das verbleibende neunte Kästchen mit 90%-iger Wahrscheinlichkeit eine Goldmünze.
Kästchen mit Goldmünzen geöffnet, so enthält auch das verbleibende neunte Kästchen mit 90%-iger Wahrscheinlichkeit eine Goldmünze.
Wurde in der gleichen Schubladenanordnung von ![]() Münzen je Schublade ein Kästchen mit Goldmünze gewählt und geöffnet, so enthalten die ungeöffneten
Münzen je Schublade ein Kästchen mit Goldmünze gewählt und geöffnet, so enthalten die ungeöffneten ![]() Kästchen mit 20%-iger Wahrscheinlichkeit sämtlich Goldmünzen, aber nur mit der Chance
Kästchen mit 20%-iger Wahrscheinlichkeit sämtlich Goldmünzen, aber nur mit der Chance ![]() durchweg Silbermünzen.
durchweg Silbermünzen.
Hat man unter ![]() Schubladen mit jeweils
Schubladen mit jeweils ![]() Kästchen nach Auswahlvorschrift zwei Goldkästchen geöffnet, so liegen in den beiden anderen Kästchen mit 60%-iger Wahrscheinlichkeit ebenfalls Goldmünzen. Die Chance, dort zwei Silbermünzen zu finden ist dagegen nur 10%. Mit 30%-iger Wahrscheinlichkeit wird man eine Silber- und eine Goldmünze entdecken.
Kästchen nach Auswahlvorschrift zwei Goldkästchen geöffnet, so liegen in den beiden anderen Kästchen mit 60%-iger Wahrscheinlichkeit ebenfalls Goldmünzen. Die Chance, dort zwei Silbermünzen zu finden ist dagegen nur 10%. Mit 30%-iger Wahrscheinlichkeit wird man eine Silber- und eine Goldmünze entdecken.
Wurden in der Schubladenanordnung von ![]() Münzen je Schublade nach Auswahlvorschrift 4 Kästchen mit Goldmünzen geöffnet, so liegen in den anderen
Münzen je Schublade nach Auswahlvorschrift 4 Kästchen mit Goldmünzen geöffnet, so liegen in den anderen ![]() Kästchen mit ca. 55,5%-iger Wahrscheinlichkeit ebenfalls Goldmünzen. Die Chance, dort durchweg Silbermünzen zu finden ist dagegen nur
Kästchen mit ca. 55,5%-iger Wahrscheinlichkeit ebenfalls Goldmünzen. Die Chance, dort durchweg Silbermünzen zu finden ist dagegen nur ![]() . Mit gut 43%-iger Wahrscheinlichkeit wird man in diesen vier Kästchen sowohl auf Silber- wie auf Goldmünzen stoßen.
. Mit gut 43%-iger Wahrscheinlichkeit wird man in diesen vier Kästchen sowohl auf Silber- wie auf Goldmünzen stoßen.
| Anzahl | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Anzahl | 1 | 1/2 | |||||||||
| 2 | 1/3 | 2/3 | |||||||||
| 3 | 1/4 | 1/2 | 3/4 | ||||||||
| 4 | 1/5 | 2/5 | 3/5 | 4/5 | |||||||
| 5 | 1/6 | 1/3 | 1/2 | 2/3 | 5/6 | ||||||
| 6 | 1/7 | 2/7 | 3/7 | 4/7 | 5/7 | 6/7 | |||||
| 7 | 1/8 | 1/4 | 3/8 | 1/2 | 5/8 | 3/4 | 7/8 | ||||
| 8 | 1/9 | 2/9 | 1/3 | 4/9 | 5/9 | 2/3 | 7/9 | 8/9 | |||
| 9 | 1/10 | 1/5 | 3/10 | 2/5 | 1/2 | 3/5 | 7/10 | 4/5 | 9/10 | ||
| 10 | 1/11 | 2/11 | 3/11 | 4/11 | 5/11 | 6/11 | 7/11 | 8/11 | 9/11 | 10/11 |
Tabelle 2‑5
2.5 Abwandlung des verallgemeinerten Paradoxons
- (5) Voraussetzungen wie in Aufgabe (4):
- Man zieht zufällig eine Schublade, öffnet zufällig
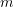 der Kästchen und findet jeweils eine Goldmünze (Ereignis
der Kästchen und findet jeweils eine Goldmünze (Ereignis 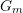 ).
). - Mit welcher Wahrscheinlichkeit enthalten die nächsten
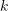 zufällig geöffneten Kästchen jeweils Silbermünzen (Ereignis
zufällig geöffneten Kästchen jeweils Silbermünzen (Ereignis 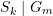 ) bzw. jeweils Goldmünzen (Ereignis
) bzw. jeweils Goldmünzen (Ereignis 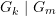 )?
)?
Befinden sich in einer Schublade ![]() Silbermünzen, so gibt es
Silbermünzen, so gibt es ![]() Möglichkeiten,
Möglichkeiten, ![]() davon auszuwählen. Betrachten wir wie oben die Schubladen
davon auszuwählen. Betrachten wir wie oben die Schubladen ![]() . usw. mit mindestens
. usw. mit mindestens ![]() Goldmünzen. In Schublade
Goldmünzen. In Schublade ![]() . wobei
. wobei ![]() zwischen
zwischen ![]() und
und ![]() liegt, gibt es demnach
liegt, gibt es demnach ![]() Möglichkeiten, unter den
Möglichkeiten, unter den ![]() Kästchen mit Goldmünzen genau
Kästchen mit Goldmünzen genau ![]() auszuwählen und zu öffnen. In jedem dieser Fälle hat man dabei
auszuwählen und zu öffnen. In jedem dieser Fälle hat man dabei ![]() Möglichkeiten,
Möglichkeiten, ![]() Kästchen mit Silbermünzen zu öffnen. Insgesamt ist daher die Anzahl der Möglichkeiten, in Schublade
Kästchen mit Silbermünzen zu öffnen. Insgesamt ist daher die Anzahl der Möglichkeiten, in Schublade ![]() zunächst
zunächst ![]() Kästchen mit Goldmünzen und danach
Kästchen mit Goldmünzen und danach ![]() Kästchen mit Silbermünzen vorzufinden
Kästchen mit Silbermünzen vorzufinden
(15) ![]()
Über alle betreffenden Schubladen ![]() . … summiert, ergeben sich demzufolge
. … summiert, ergeben sich demzufolge
(16) 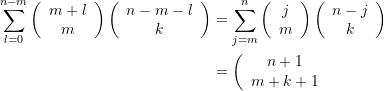
Fälle, in denen jeweils ![]() Kästchen mit Silbermünzen gefunden werden. Die Summenbildung kann hier bei
Kästchen mit Silbermünzen gefunden werden. Die Summenbildung kann hier bei ![]() abgebrochen werden, weil für
abgebrochen werden, weil für ![]() die Summanden verschwinden.
die Summanden verschwinden.
Die gesamte Anzahl der Möglichkeiten, nach dem Öffnen von ![]() Kästchen mit einer Goldmünze überhaupt
Kästchen mit einer Goldmünze überhaupt ![]() Kästchen (mit irgendeiner Münze) zu finden, ist entsprechend
Kästchen (mit irgendeiner Münze) zu finden, ist entsprechend
(17) ![]()
Die fragliche Wahrscheinlichkeit ![]() ergibt sich deswegen zu
ergibt sich deswegen zu
(18) 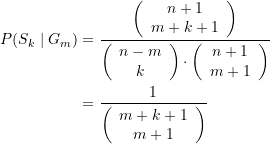
Es zeigt sich, dass die Wahrscheinlichkeit, nach Öffnen von ![]() Kästchen mit Goldmünzen
Kästchen mit Goldmünzen ![]() Silbermünzen zu finden von der Gesamtanzahl
Silbermünzen zu finden von der Gesamtanzahl ![]() der Münzen pro Schublade unabhängig ist, sofern nur
der Münzen pro Schublade unabhängig ist, sofern nur ![]() gilt. Im Grenzfall
gilt. Im Grenzfall ![]() erhalten wir wieder das obige Resultat (s. Tabelle 2‑4). Einen Überblick zu den erhaltenen Wahrscheinlichkeiten für
erhalten wir wieder das obige Resultat (s. Tabelle 2‑4). Einen Überblick zu den erhaltenen Wahrscheinlichkeiten für ![]() Goldmünzen und
Goldmünzen und ![]() zu öffnenden Kästchen mit Silbermünzen gibt Tabelle 2‑6.
zu öffnenden Kästchen mit Silbermünzen gibt Tabelle 2‑6.
| Anzahl | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Anzahl | 1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | 1/8 | 1/9 | 1/10 | 1/11 |
| 2 | 1/3 | 1/6 | 1/10 | 1/15 | 1/21 | 1/28 | 1/36 | 1/45 | 1/55 | 1/66 | |
| 3 | 1/4 | 1/10 | 1/20 | 1/35 | 1/56 | 1/84 | 1/120 | 1/165 | 1/220 | 1/286 | |
| 4 | 1/5 | 1/15 | 1/35 | 1/70 | 1/126 | 1/210 | 1/330 | 1/495 | 1/715 | 1/1001 | |
| 5 | 1/6 | 1/21 | 1/56 | 1/126 | 1/252 | 1/462 | 1/792 | 1/1287 | 1/2002 | 1/3003 | |
| 6 | 1/7 | 1/28 | 1/84 | 1/210 | 1/462 | 1/924 | 1/1716 | 1/3003 | 1/5005 | 1/8008 | |
| 7 | 1/8 | 1/36 | 1/120 | 1/330 | 1/792 | 1/1716 | 1/3432 | 1/6435 | 1/11440 | 1/19448 | |
| 8 | 1/9 | 1/45 | 1/165 | 1/495 | 1/1287 | 1/3003 | 1/6435 | 1/12870 | 1/24310 | 1/43785 | |
| 9 | 1/10 | 1/55 | 1/220 | 1/715 | 1/2002 | 1/5005 | 1/11440 | 1/24310 | 1/48620 | 1/92378 | |
| 10 | 1/11 | 1/66 | 1/286 | 1/1001 | 1/3003 | 1/8008 | 1/19448 | 1/43785 | 1/92378 | 1/184756 |
Tabelle 2‑6
Der Tabelle kann man bemerkenswerte Resultate entnehmen. Greifen wir uns einige davon heraus:
Hat man eine Goldmünze gefunden, so enthält ein daraufhin geöffnetes Kästchen mit der Chance ![]() eine Silbermünze und demnach mit der Wahrscheinlichkeit
eine Silbermünze und demnach mit der Wahrscheinlichkeit ![]() wieder eine Goldmünze.
wieder eine Goldmünze.
Wurden zunächst gar ![]() Kästchen mit Goldmünzen geöffnet, so enthält das nächste gewählte Kästchen mit der Chance
Kästchen mit Goldmünzen geöffnet, so enthält das nächste gewählte Kästchen mit der Chance ![]() eine Silbermünze und demnach mit der Wahrscheinlichkeit 90% eine Goldmünze.
eine Silbermünze und demnach mit der Wahrscheinlichkeit 90% eine Goldmünze.
Hat man zwei Goldkästchen geöffnet, so befinden sich in den daraufhin geöffneten zwei weiteren Kästchen mit 10%-iger Wahrscheinlichkeit Silbermünzen. Die Chance, in diesen beiden Kästchen zumindest einmal auf eine Goldmünze zu stoßen liegt demnach bei 90%.
Wurden ![]() Kästchen mit Goldmünzen geöffnet, so liegen in den nächsten vier gewählten Kästchen mit der Chance
Kästchen mit Goldmünzen geöffnet, so liegen in den nächsten vier gewählten Kästchen mit der Chance ![]() jeweils Silbermünzen. Mit einer Wahrscheinlichkeit von ca. 99,9% findet sich aber in einem dieser vier Kästchen eine Goldmünze.
jeweils Silbermünzen. Mit einer Wahrscheinlichkeit von ca. 99,9% findet sich aber in einem dieser vier Kästchen eine Goldmünze.
Und dies alles unabhängig von der Anzahl der Münzen pro Schublade (nur ![]() vorausgesetzt).
vorausgesetzt).
Behandeln wir nun noch die Frage, mit welcher Wahrscheinlichkeit die ![]() zufällig geöffneten Kästchen jeweils Gold- statt Silbermünzen enthalten (Ereignis
zufällig geöffneten Kästchen jeweils Gold- statt Silbermünzen enthalten (Ereignis ![]() ).
).
In jedem der ![]() Fälle, wenn in den Schubladen
Fälle, wenn in den Schubladen ![]() . mit
. mit ![]() zwischen
zwischen ![]() und
und ![]() . unter den
. unter den ![]() Kästchen mit Goldmünzen zunächst
Kästchen mit Goldmünzen zunächst ![]() Kästchen geöffnet wurden, hat man
Kästchen geöffnet wurden, hat man ![]() Möglichkeiten, zusätzlich
Möglichkeiten, zusätzlich ![]() Kästchen mit Goldmünzen zu finden. Insgesamt ist daher die Anzahl der Möglichkeiten, in Schublade
Kästchen mit Goldmünzen zu finden. Insgesamt ist daher die Anzahl der Möglichkeiten, in Schublade ![]() zunächst
zunächst ![]() Kästchen mit Goldmünzen und danach nochmals
Kästchen mit Goldmünzen und danach nochmals ![]() Kästchen mit Goldmünzen zu entdecken
Kästchen mit Goldmünzen zu entdecken
(19) ![]()
Über alle Schubladen ![]() … summiert, erhalten wir demnach
… summiert, erhalten wir demnach
(20) 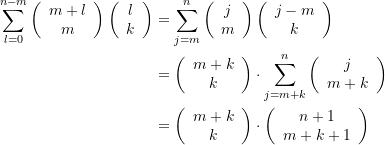
Möglichkeiten zum Auffinden von ![]() Kästchen mit Goldmünzen. Die Summenbildung beginnt hier bei
Kästchen mit Goldmünzen. Die Summenbildung beginnt hier bei ![]() . weil für
. weil für ![]() die Summanden verschwinden.
die Summanden verschwinden.
Nach der oben bestimmten Gesamtanzahl ![]() der Möglichkeiten, nach dem Öffnen von
der Möglichkeiten, nach dem Öffnen von ![]() Kästchen mit einer Goldmünze überhaupt
Kästchen mit einer Goldmünze überhaupt ![]() Kästchen (mit irgendeiner Münze) zu finden, folgt die fragliche Wahrscheinlichkeit
Kästchen (mit irgendeiner Münze) zu finden, folgt die fragliche Wahrscheinlichkeit ![]() zu
zu
(21) 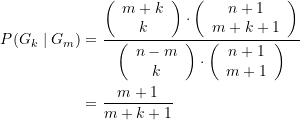
Die Wahrscheinlichkeit, nach Öffnen von ![]() Kästchen mit Goldmünzen nochmals
Kästchen mit Goldmünzen nochmals ![]() Kästchen mit Goldmünzen zu finden, ist demnach von der Gesamtanzahl
Kästchen mit Goldmünzen zu finden, ist demnach von der Gesamtanzahl ![]() der Münzen pro Schublade unabhängig, sofern nur
der Münzen pro Schublade unabhängig, sofern nur ![]() gilt. Im Grenzfall
gilt. Im Grenzfall ![]() erhalten wir wieder das obige Resultat (s. Tabelle 2‑5).
erhalten wir wieder das obige Resultat (s. Tabelle 2‑5).
Tabelle 2‑7 kann man im Überblick die aus der Formelbeziehung folgenden Wahrscheinlichkeiten für ![]() Goldmünzen und
Goldmünzen und ![]() weiteren zu öffnenden Kästchen mit Goldmünzen entnehmen.
weiteren zu öffnenden Kästchen mit Goldmünzen entnehmen.
| Anzahl | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Anzahl | 1 | 1/2 | 2/3 | 3/4 | 4/5 | 5/6 | 6/7 | 7/8 | 8/9 | 9/10 | 10/11 |
| 2 | 1/3 | 1/2 | 3/5 | 2/3 | 5/7 | 3/4 | 7/9 | 4/5 | 9/11 | 5/6 | |
| 3 | 1/4 | 2/5 | 1/2 | 4/7 | 5/8 | 2/3 | 7/10 | 8/11 | 3/4 | 10/13 | |
| 4 | 1/5 | 1/3 | 3/7 | 1/2 | 5/9 | 3/5 | 7/11 | 2/3 | 9/13 | 5/7 | |
| 5 | 1/6 | 2/7 | 3/8 | 4/9 | 1/2 | 6/11 | 7/12 | 8/13 | 9/14 | 2/3 | |
| 6 | 1/7 | 1/4 | 1/3 | 2/5 | 5/11 | 1/2 | 7/13 | 4/7 | 3/5 | 5/8 | |
| 7 | 1/8 | 2/9 | 3/10 | 4/11 | 5/12 | 6/13 | 1/2 | 8/15 | 9/16 | 10/17 | |
| 8 | 1/9 | 1/5 | 3/11 | 1/3 | 5/13 | 3/7 | 7/15 | 1/2 | 9/17 | 5/9 | |
| 9 | 1/10 | 2/11 | 1/4 | 4/13 | 5/14 | 2/5 | 7/16 | 8/17 | 1/2 | 10/19 | |
| 10 | 1/11 | 1/6 | 3/13 | 2/7 | 1/3 | 3/8 | 7/17 | 4/9 | 9/19 | 1/2 |
Tabelle 2‑7
Einige Resultate seien wieder gesondert herausgehoben (zum Vergleich s. a. Tabelle 2‑6):
Hat man eine Goldmünze gefunden, so enthält ein daraufhin geöffnetes Kästchen mit der Chance ![]() wieder eine Goldmünze.
wieder eine Goldmünze.
Wurden zunächst gar ![]() Kästchen mit Goldmünzen geöffnet, so findet man in den nächsten
Kästchen mit Goldmünzen geöffnet, so findet man in den nächsten ![]() gewählten Kästchen mit der Chance 60% durchweg Goldmünzen.
gewählten Kästchen mit der Chance 60% durchweg Goldmünzen.
Hat man zwei Goldkästchen geöffnet, so befinden sich in den daraufhin geöffneten zwei weiteren Kästchen mit 60%-iger Wahrscheinlichkeit ebenfalls Goldmünzen.
Wurden ![]() Kästchen mit Goldmünzen geöffnet, so liegen in den nächsten vier gewählten Kästchen mit der Chance
Kästchen mit Goldmünzen geöffnet, so liegen in den nächsten vier gewählten Kästchen mit der Chance ![]() jeweils Silbermünzen. Mit einer Wahrscheinlichkeit von ca. 99,9% findet sich daher in einem dieser vier Kästchen eine Goldmünze. Die Chance, dort durchweg Goldmünzen zu entdecken liegt bei ca. 71% (
jeweils Silbermünzen. Mit einer Wahrscheinlichkeit von ca. 99,9% findet sich daher in einem dieser vier Kästchen eine Goldmünze. Die Chance, dort durchweg Goldmünzen zu entdecken liegt bei ca. 71% (![]() ).
).
Die Anzahl der Münzen pro Schublade ist dabei nicht relevant (nur ![]() vorausgesetzt).
vorausgesetzt).
2.6 Zusammenfassung zum verallgemeinerten Kästchenparadoxon
Die erhaltenen Formeln zur Bestimmung der betreffenden Wahrscheinlichkeiten sind in Tabelle 2‑8 aufgelistet.
| Problemstellung im Rahmen von Aufgabe (4) und (5) | Formel | Beispiel | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
Tabelle 2‑8
2.7 Weitere Varianten
Allen betrachteten Varianten zum Kästchenparadoxon gemeinsam ist die gleichmäßige Verteilung der Münzen auf die Schubladen und die regelgerechte Bestückung von jeweils ![]() Kästchen mit Goldmünzen. In der Problembehandlung hatten wir gesehen, dass dies, ungeachtet der zufälligen Auswahl der Kästchen, von großer Bedeutung für die resultierenden Wahrscheinlichkeiten ist. Geht man im konkreten Falle ohne die spezifische Verteilung auf Schubladen von der gleichen Anzahl von Kästchen mit Gold- und Silbermünzen aus, so erhält man z. T völlig verschiedene Ergebnisse.
Kästchen mit Goldmünzen. In der Problembehandlung hatten wir gesehen, dass dies, ungeachtet der zufälligen Auswahl der Kästchen, von großer Bedeutung für die resultierenden Wahrscheinlichkeiten ist. Geht man im konkreten Falle ohne die spezifische Verteilung auf Schubladen von der gleichen Anzahl von Kästchen mit Gold- und Silbermünzen aus, so erhält man z. T völlig verschiedene Ergebnisse.
Im Folgenden betrachten wir eine andersartige Verteilung der Gold- und Silbermünzen auf die Schubladen.
- (6) Wir haben
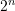 Schubladen mit jeweils
Schubladen mit jeweils  Kästchen:
Kästchen: - Die Schubladen tragen die Nummern
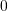 bis
bis  . In jeder Schublade befinden sich
. In jeder Schublade befinden sich  Kästchen, in jedem Kästchen liegt eine Gold- oder eine Silbermünze.
Kästchen, in jedem Kästchen liegt eine Gold- oder eine Silbermünze. - Jede Schublade enthält genau die Anzahl an Kästchen mit Goldmünzen, wie in der Binärdarstellung der Schubladennummer Einsen auftreten. Die restlichen Kästchen enthalten jeweils Silbermünzen.
- Man zieht zufällig eine Schublade, öffnet m der Kästchen und findet jeweils eine Goldmünze (Ereignis
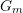 ).
). - Mit welcher Wahrscheinlichkeit tritt das vorstehende Ereignis
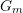 ein?
ein? - Mit welcher Wahrscheinlichkeit befinden sich in den anderen Kästchen jeweils Silbermünzen (Ereignis
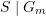 )?
)? - Mit welcher Wahrscheinlichkeit befinden sich in den anderen Kästchen jeweils Goldmünzen (Ereignis
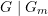 )?
)? - Mit welcher Wahrscheinlichkeit befinden sich in den nächsten k zufällig geöffneten Kästchen jeweils Silbermünzen (Ereignis
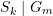 )?
)? - Mit welcher Wahrscheinlichkeit befinden sich in den nächsten k zufällig geöffneten Kästchen jeweils Goldmünzen (Ereignis
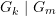 )?
)?
Die Anordnung der Kästchen mit Münzen im vorstehenden Problem kann wie folgt veranschaulicht werden.

Betrachten wir zunächst das Ereignis ![]() .
.
Es gibt genau ![]() Möglichkeiten
Möglichkeiten ![]() von insgesamt
von insgesamt ![]() Kästchen mit Goldmünzen zu bestücken. Jeder dieser Fälle entspricht genau einer Schublade aus der obigen Anordnung. Lassen wir nun
Kästchen mit Goldmünzen zu bestücken. Jeder dieser Fälle entspricht genau einer Schublade aus der obigen Anordnung. Lassen wir nun ![]() von
von ![]() bis
bis ![]() laufen, so erhalten wir demnach alle Schubladen mit mindestens
laufen, so erhalten wir demnach alle Schubladen mit mindestens ![]() Goldkästchen. In jeder dieser Schubladen gibt es
Goldkästchen. In jeder dieser Schubladen gibt es ![]() Möglichkeiten, unter den
Möglichkeiten, unter den ![]() Kästchen mit Goldmünzen genau
Kästchen mit Goldmünzen genau ![]() auszuwählen und zu öffnen. Daher beläuft sich, über alle Schubladen mit mindestens m Goldmünzen gerechnet, die Anzahl der Möglichkeiten,
auszuwählen und zu öffnen. Daher beläuft sich, über alle Schubladen mit mindestens m Goldmünzen gerechnet, die Anzahl der Möglichkeiten, ![]() Kästchen mit Goldmünzen zu wählen auf die Summe
Kästchen mit Goldmünzen zu wählen auf die Summe
(22) 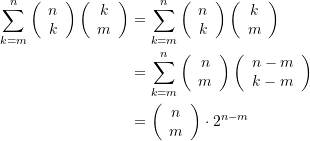
Andererseits ist die Gesamtanzahl der Fälle, in irgendeiner Schublade überhaupt ![]() von
von ![]() Kästchen zu wählen gleich
Kästchen zu wählen gleich ![]() . Damit bekommen wir die Wahrscheinlichkeit
. Damit bekommen wir die Wahrscheinlichkeit ![]() für die Realisierung des Ereignisses
für die Realisierung des Ereignisses ![]() zu
zu
(23) 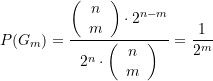
Die Wahrscheinlichkeit zum Auffinden von ![]() Kästchen mit Goldmünzen ist demzufolge auch hier, wie im Originalproblem, unabhängig von der Anzahl der Münzen pro Schublade bzw. der Schubladenanzahl (natürlich vorausgesetzt, es befinden sich in jeder Schublade mindestens
Kästchen mit Goldmünzen ist demzufolge auch hier, wie im Originalproblem, unabhängig von der Anzahl der Münzen pro Schublade bzw. der Schubladenanzahl (natürlich vorausgesetzt, es befinden sich in jeder Schublade mindestens ![]() Münzen).
Münzen).
Wenden wir uns nun dem bedingten Ereignis ![]() zu und fragen nach der Chance, nach dem Auffinden von m Kästchen mit Goldmünzen in den übrigen Kästchen stets Silbermünzen zu entdecken. Offensichtlich kann man jedenfalls nur in den Schubladen mit
zu und fragen nach der Chance, nach dem Auffinden von m Kästchen mit Goldmünzen in den übrigen Kästchen stets Silbermünzen zu entdecken. Offensichtlich kann man jedenfalls nur in den Schubladen mit ![]() Goldmünzen nach dem Öffnen von
Goldmünzen nach dem Öffnen von ![]() Kästchen mit Goldmünzen in den restlichen
Kästchen mit Goldmünzen in den restlichen ![]() Kästchen jeweils Silbermünzen vorfinden. Unter allen denkbaren Auswahlmöglichkeiten gibt es nur in diesen Schubladen die Realisierungschance für das fragliche Ereignis („ein Schublade wird gewählt, es werden
Kästchen jeweils Silbermünzen vorfinden. Unter allen denkbaren Auswahlmöglichkeiten gibt es nur in diesen Schubladen die Realisierungschance für das fragliche Ereignis („ein Schublade wird gewählt, es werden ![]() Kästchen mit Goldmünzen gefunden, in den verbleibenden
Kästchen mit Goldmünzen gefunden, in den verbleibenden ![]() Kästchen befinden sich Silbermünzen“), und zwar genau einmal pro Schublade. Wie bereits gezeigt, existieren
Kästchen befinden sich Silbermünzen“), und zwar genau einmal pro Schublade. Wie bereits gezeigt, existieren ![]() solche Schubladen.
solche Schubladen.
Die Anzahl der Möglichkeiten zur Auswahl vom ![]() Goldmünzen haben wir oben zu
Goldmünzen haben wir oben zu ![]() bestimmt. Insgesamt erhalten wir daher die fragliche Wahrscheinlichkeit zu
bestimmt. Insgesamt erhalten wir daher die fragliche Wahrscheinlichkeit zu
(24) ![]()
Es ist dies die (bedingte) Wahrscheinlichkeit dafür, „in den restlichen ![]() Kästchen Silbermünzen zu finden“, wenn in derselben Schublade zuvor „
Kästchen Silbermünzen zu finden“, wenn in derselben Schublade zuvor „![]() Kästchen mit Goldmünzen geöffnet worden waren“.
Kästchen mit Goldmünzen geöffnet worden waren“.
Fragen wir weiter nach der Wahrscheinlichkeit, ![]() Gold- statt Silbermünzen vorzufinden (das ist das Ereignis
Gold- statt Silbermünzen vorzufinden (das ist das Ereignis ![]() ), so erhalten wir auch hier
), so erhalten wir auch hier
(25) 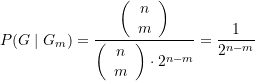
da ja nur in einer Schublade, nämlich in Nummer 2n-1, tatsächlich ![]() Goldkästchen vorkommen, wobei allerdings bei jeder der
Goldkästchen vorkommen, wobei allerdings bei jeder der ![]() Möglichkeiten zur Auswahl von
Möglichkeiten zur Auswahl von ![]() Goldmünzen auch die übrigen Kästchen Goldmünzen enthalten.
Goldmünzen auch die übrigen Kästchen Goldmünzen enthalten.
Bei den verbleibenden Ereignissen ![]() und
und ![]() geht es darum, in jeweils
geht es darum, in jeweils ![]() zufällig gewählten weiteren Kästchen Silber- bzw. Goldmünzen zu entdecken, wenn in derselben Schublade zuvor
zufällig gewählten weiteren Kästchen Silber- bzw. Goldmünzen zu entdecken, wenn in derselben Schublade zuvor ![]() Kästchen mit Goldmünzen geöffnet worden waren.
Kästchen mit Goldmünzen geöffnet worden waren.
Offensichtlich kann man in den Schubladen mit ![]() Goldmünzen nur dann
Goldmünzen nur dann ![]() Kästchen mit Silbermünzen antreffen, wenn
Kästchen mit Silbermünzen antreffen, wenn ![]() die Gesamtanzahl der Münzen pro Schublade nicht übersteigt. Es gibt jeweils
die Gesamtanzahl der Münzen pro Schublade nicht übersteigt. Es gibt jeweils ![]() solcher Schubladen und in jeder davon
solcher Schubladen und in jeder davon ![]() Auswahlmöglichkeiten zum Öffnen von
Auswahlmöglichkeiten zum Öffnen von ![]() Kästchen mit Silbermünzen. In der gleichen Situation gibt es
Kästchen mit Silbermünzen. In der gleichen Situation gibt es ![]() Möglichkeiten, in welchen
Möglichkeiten, in welchen ![]() Kästchen mit Goldmünzen gefunden werden sowie insgesamt die Anzahl
Kästchen mit Goldmünzen gefunden werden sowie insgesamt die Anzahl ![]() Möglichkeiten,
Möglichkeiten, ![]() irgendwelche Kästchen zu öffnen.
irgendwelche Kästchen zu öffnen.
Summiert über alle betreffenden Schubladen mit ![]() … Goldkästchen, erhalten wir deshalb
… Goldkästchen, erhalten wir deshalb
(26) 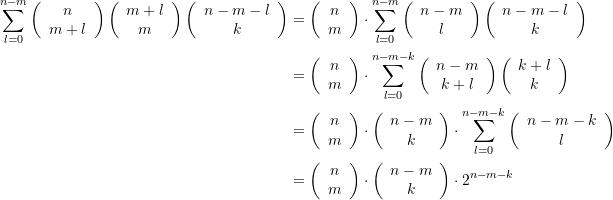
Fälle, in denen jeweils ![]() Kästchen mit Silbermünzen gefunden werden. Auf der anderen Seite beläuft sich die Anzahl der Möglichkeiten, in der gleichen Situation überhaupt
Kästchen mit Silbermünzen gefunden werden. Auf der anderen Seite beläuft sich die Anzahl der Möglichkeiten, in der gleichen Situation überhaupt ![]() Kästchen zu öffnen auf
Kästchen zu öffnen auf
(27) 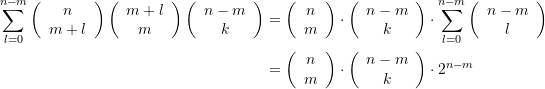
Die Wahrscheinlichkeit ![]() ergibt sich folglich zu
ergibt sich folglich zu
(28) ![]()
Entsprechend finden wir für das Ereignis, ![]() Goldmünzen zu entdecken, nachdem zuvor
Goldmünzen zu entdecken, nachdem zuvor ![]() Kästchen Goldmünzen geöffnet worden waren,
Kästchen Goldmünzen geöffnet worden waren,
(29) 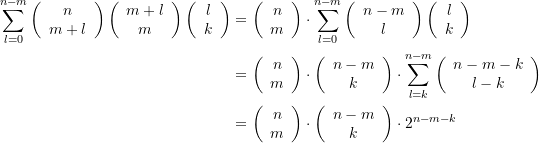
Somit bekommen wir für die Wahrscheinlichkeit ![]() die gleiche Formel wie für
die gleiche Formel wie für ![]() :
:
(30) ![]()
Die erhaltenen Formeln zur Bestimmung der Wahrscheinlichkeiten sind in Tabelle 2‑9 zusammenfassend aufgelistet.
Man entnimmt der Tabelle, dass die Wahrscheinlichkeiten in allen Fällen gleichartig nur von der Anzahl der zu öffnenden Kästchen abhängen, völlig unabhängig davon, wie viele Kästchen bereits geöffnet worden sind. Pro zu öffnendem Kästchen kommt einfach der Faktor ![]() hinzu. Warum ist das so? Nun, die Erklärung ist einfach. Im obigen Schema wurde bereits angedeutet, wie man die
hinzu. Warum ist das so? Nun, die Erklärung ist einfach. Im obigen Schema wurde bereits angedeutet, wie man die ![]() Kästchen pro Schublade mit Gold- und Silbermünzen bestückt, um den Voraussetzungen der Aufgabe Rechnung zu tragen. Tatsächlich kommen in den
Kästchen pro Schublade mit Gold- und Silbermünzen bestückt, um den Voraussetzungen der Aufgabe Rechnung zu tragen. Tatsächlich kommen in den ![]() Schubladen genau die
Schubladen genau die ![]() möglichen Fälle für die Kombinationen von Gold- und Silbermünzen entsprechend der Zahlen
möglichen Fälle für die Kombinationen von Gold- und Silbermünzen entsprechend der Zahlen ![]() bis
bis ![]() vor. In jeder Kästchenposition innerhalb einer Schublade findet sich daher in der Hälfte der Fälle eine Goldmünze (bzw. eine Silbermünze). Das heißt, beim Öffnen eines beliebigen Kästchens ist die Chance, auf eine Goldmünze zu treffen, stets 50%. Jede Schublade ist daher ein gleichwahrscheinliches Muster für die mögliche Auswahl von
vor. In jeder Kästchenposition innerhalb einer Schublade findet sich daher in der Hälfte der Fälle eine Goldmünze (bzw. eine Silbermünze). Das heißt, beim Öffnen eines beliebigen Kästchens ist die Chance, auf eine Goldmünze zu treffen, stets 50%. Jede Schublade ist daher ein gleichwahrscheinliches Muster für die mögliche Auswahl von ![]() Kästchen mit Gold- und Silbermünzen. Die Auswahl einer Schublade entspricht folglich dem Ereignis, in
Kästchen mit Gold- und Silbermünzen. Die Auswahl einer Schublade entspricht folglich dem Ereignis, in ![]() Kästchen zufällig Gold- bzw. Silbermünzen zu hineinzulegen. Oder, noch einfacher, eine Münze
Kästchen zufällig Gold- bzw. Silbermünzen zu hineinzulegen. Oder, noch einfacher, eine Münze ![]() mal zu werfen und entsprechend Kopf (=Gold) und Zahl (=Silber) zu notieren. Im letzten Bild sieht man natürlich sofort, dass die Wahrscheinlichkeit für beliebige Sequenzen von
mal zu werfen und entsprechend Kopf (=Gold) und Zahl (=Silber) zu notieren. Im letzten Bild sieht man natürlich sofort, dass die Wahrscheinlichkeit für beliebige Sequenzen von ![]() -mal Kopf oder
-mal Kopf oder ![]() -mal Zahl eben gleich
-mal Zahl eben gleich ![]() ist, unabhängig davon, wie oft zuvor Kopf oder Zahl gefallen waren.
ist, unabhängig davon, wie oft zuvor Kopf oder Zahl gefallen waren.
| Problemstellung im Rahmen von Aufgabe (6) | Formel | Beispiel | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
| Wahrscheinlichkeit | | | |
Tabelle 2‑9



![Rendered by QuickLaTeX.com \[\frac{1}{{\left( {\begin{array}{{c}} {n+1} \\ {m+1} \end{array}} \right)}}\]](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-48c6ce41d3715d074c00d1b82f274c9a_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{{\left( {\begin{array}{{c}} {m+k+1} \\ {m+1} \end{array}} \right)}}\]](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-efa24bde0987dc4519ccfdb70fb1e6de_l3.png)
Danke für die ausführliche Erläuterung!
Bei der Berechnung von P(S|G) in Abschnitt 2.2 zwischen Tabelle 2-2 und Tabelle 2-3 müsste es P(S|G)=…=(1/4)x(2/1)=(1/2) heißen anstelle von P(S|G)=…=(1/4)x(1/2)=(1/2)
Vielen Dank für den Hinweis. Ist korrigiert!