-
Gronwall-Verfahren
Das Gronwall-Verfahren dient zur Summierung von konvergenten und divergenten unendlichen Reihen und wird definiert auf der Basis von konformen Abbildungen. Das Summationsverfahren arbeitet mit geeigneten analytischen Funktionen
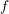 und
und 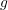 von denen insbesondere verlangt wird, dass sie auf dem abgeschlossenen Einheitskreis
von denen insbesondere verlangt wird, dass sie auf dem abgeschlossenen Einheitskreis 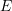 (mit Ausnahme des Punktes
(mit Ausnahme des Punktes 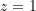 ) holomorph sind. Von
) holomorph sind. Von 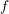 wird darüber hinaus Injektivität und
wird darüber hinaus Injektivität und 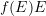 erwartet, zudem
erwartet, zudem 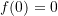 und
und 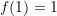 . Eine Voraussetzung an die Funktion
. Eine Voraussetzung an die Funktion 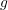 ist
ist 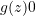 für alle
für alle 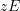 , außerdem hat
, außerdem hat 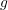 an der Stelle
an der Stelle 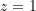 eine Singularität.
eine Singularität.⇒ Gronwall-Verfahren
——————————————
-
Eine Theorie komplexwertiger Abelscher Limitierungsmethoden
Ausgehend von einer geeigneten Potenzreihe
![Rendered by QuickLaTeX.com \[P(z)=\sum\limits_{{n=0}}^{\infty }{{{{p}_{n}}{{z}^{n}}}}\]](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-7cf6c0989f170fc2c54c8752db6f1f17_l3.png)
definieren wir Limitierung durch ein Potenzreihenverfahren über die Zuordnung
![Rendered by QuickLaTeX.com \[\underset{{n\to \infty }}{\mathop{{\lim }}}\,{{s}_{n}}:=\underset{{z\to r}}{\mathop{{\lim }}}\,\frac{1}{{P(z)}}\sum\limits_{{n=0}}^{\infty }{{{{p}_{n}}{{s}_{n}}{{z}^{n}}}}.\]](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-9a6527ea8c57fee76169ab5e9a4d213a_l3.png)
Gegenstand dieser Arbeit sind die Verfahren mit
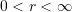 , wobei wir für den Grenzübergang komplexe Werte von
, wobei wir für den Grenzübergang komplexe Werte von  zulassen. Es wird insbesondere der Zusammenhang zwischen der Limitierungseigenschaft und der geometrischen Form des den Grenzübergang beschreibenden komplexen Gebiets untersucht.
zulassen. Es wird insbesondere der Zusammenhang zwischen der Limitierungseigenschaft und der geometrischen Form des den Grenzübergang beschreibenden komplexen Gebiets untersucht.⇒ Eine Theorie komplexwertiger Abelscher Limitierungsmethoden
—————————————


