Harmonische Brücken

Print 🖨 PDF 📄 eBook 📱

Wir stapeln gleichförmige Steine der Länge $2b$ und nummerieren sie fortlaufend von $1$ bis $n$ . Den ersten Stein legen wir mit einem kleinen Überstand an die Tischkante. Dem Stein darüber geben wir seinerseits einen kleinen Überstand über den ersten Stein hinaus, aber so, dass die beiden nicht herunterfallen. Gleichfalls legen wir den dritten Stein auf den zweiten und schieben ihn leicht über die Kante hinaus, aber wieder so, dass er nicht herunterfällt und der Stapel nicht kippt. Und so verfahren wir mit allen weiteren Steinen. Die Länge des jeweiligen Überstands eines Steins über den darunterliegenden bezeichnen wir mit $a_{n}$ . Demnach ist also $a_{1}$ die Länge, mit welcher der erste Stein über die Tischkante hinausragt und $a_{2}$ die Länge des Überstands des zweiten Steins über den ersten Stein hinaus, usw. Die Länge des Überstands des letzten, also des $n$ -ten Steins, ist demzufolge $a_{n}$ . In Abbildung 1 sind die Bezeichnungen erläutert.

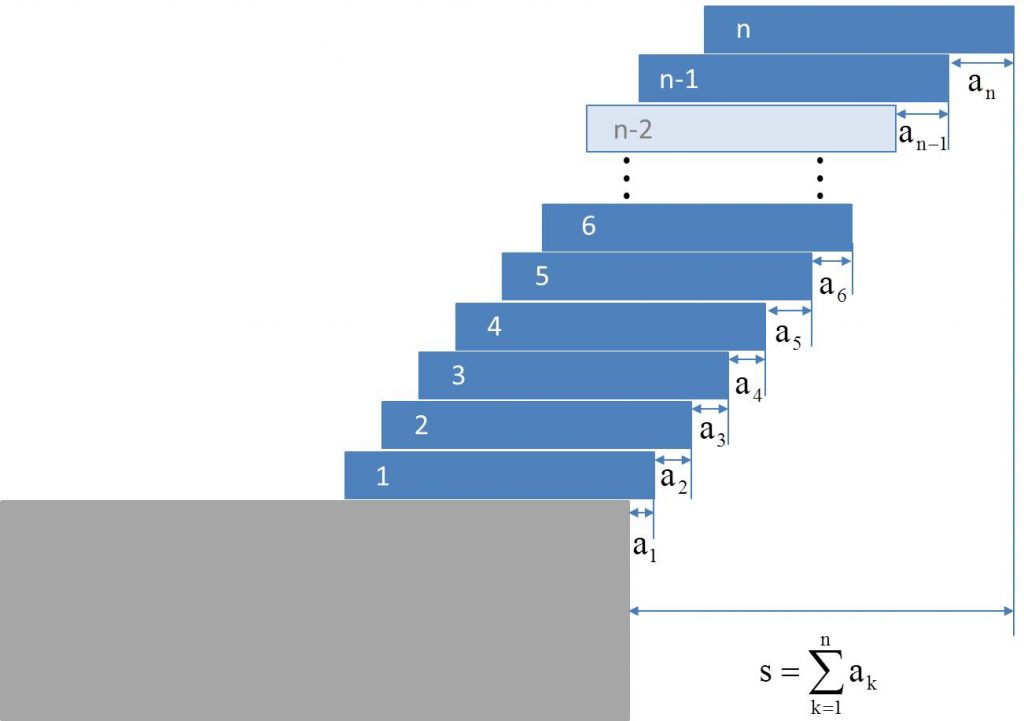
Abbildung 1

Frage: Wie weit über die Tischkante hinaus können wir den Stapel bauen? Oder, anders gefragt, welche Strecke können wir solchermaßen mit den Steinen überbrücken? Welche Spannbreite kann die Brücke erreichen: Wie groß kann $s$ maximal werden?

Offenbar können wir den ersten Stein nur maximal bis zur Hälfte seiner Länge über die Tischkante hinausschieben, also kann $a_{1}$ höchstens dem Wert $b$ erreichen. Wenn wir aber $a_{1}=b$ wählen, wie geht es dann weiter? – Leider ist das Ende bereits erreicht; $b$ ist dann der maximal mögliche Überstand für die Brücke.

Nehmen wir also für $a_{1}$ einen kleineren Wert, sagen wir $a_{1}=\frac{b}{2}$ . In diesem Falle können wir den nächsten Stein so darauf legen, dass er um den Wert $a_{2}=b$ über die jetzt durch den ersten Stein gebildete äußerste Kante hinausragt. Der gesamte Überstand der Brücke erreicht jetzt den Betrag $s = a_{1}+a_{2}=(\frac{1}{2} + 1)\cdot b=\frac{3}{2}\cdot b$ . Wenn wir nun aber einen dritten Stein darauf packen, dann kippt die Brücke sogar dann, wenn wir den Stein genau über den zweiten legen. Demnach ist in dieser Konstellation ebenfalls schon die maximale möglich Spannweite der Brücke erreicht.

Alternativ können wir fortfahren, indem wir z.B. für den ersten Stein $a_{1}=\frac{b}{3}$ wählen. Den zweiten Stein dürfen wir nun bis zum Wert $a_{2}=b$ über die durch den ersten Stein gebildete Kante hinausschieben, weiter aber nicht, sonst kippt der Brückenbau. Gewonnen haben wir damit aber noch nichts, denn der Überstand ist jetzt nur noch $s = a_{1}+a_{2}=(\frac{1}{3} + 1)\cdot b =\frac{4}{3}\cdot b$ . Und wenn wir einen weiteren Stein darauf legen, stürzt die Brücke wieder ein. Wir können aber $a_{2}=\frac{b}{2}$ nehmen. In diesem Falle haben wir die Möglichkeit, den nächsten, also den dritten Stein, mit einem Überstand von $a_{3}=b$ darauf zu legen. Der erreichte Gesamtüberstand ist jetzt $s = a_{1}+a_{2}+a_{3}=(\frac{1}{3}+\frac{1}{2} + 1)\cdot b=1\frac{5}{6}\cdot b$ .

In Abbildung 2 sind diese Beispiele dargestellt, dabei ist Schwerpunkts des Teilstapels vom jeweiligen Stein bis zum obersten Stein jeweils mit einem weißen Kreuz markiert. Liegt dieses Kreuz, bezogen auf den darunter liegenden Stein innerhalb der Auflagefläche, dann ist der Stapel stabil, liegt er außerhalb, dann stürzt der Stapel. Abbildung 2 zeigt den Grenzfall einer gerade noch stabilen Lage.

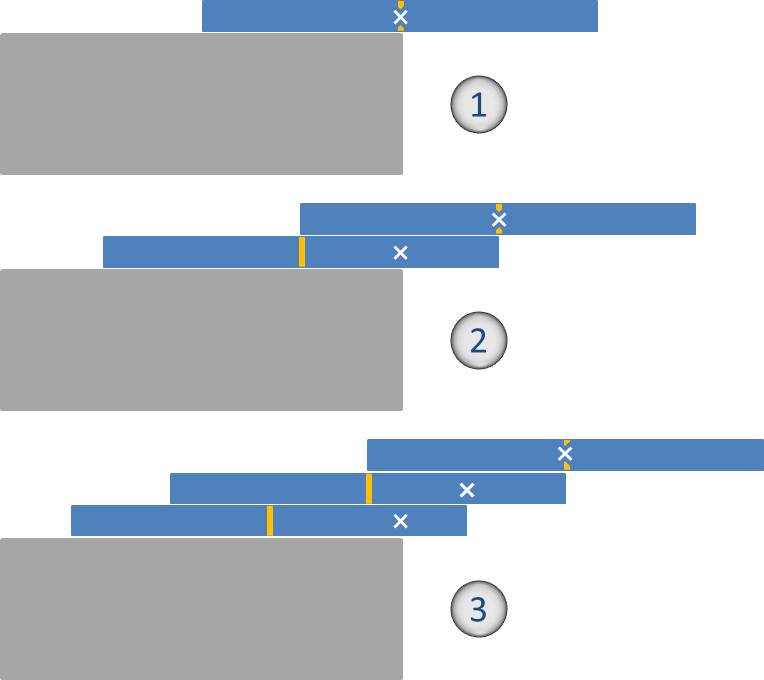
Abbildung 2

In Abbildung 3 ist der weitere Fall von 4 Steinen, die in der Abfolge $a_{1}=\frac{b}{4}$ , $a_{2}=\frac{b}{3}$ , $a_{3}=\frac{b}{2}$ , $a_{4}=\frac{b}{1}$ aufeinander gelegt werden im Detail skizziert. Zur besseren Nachvollziehbarkeit der relativen Positionierung tragen die einzelnen Steine ein Unterteilungsraster in Zehnteln der halben Länge $b$ . Der Gesamtüberstand im letzten Fall ist $s = a_{1}+a_{2}+a_{3}+a_{4}=(\frac{1}{4}+\frac{1}{3}+\frac{1}{2} + 1)\cdot b=2\frac{1}{12}\cdot b$ . Mit 4 Steinen kann man immerhin also mehr als die Länge $2b$ eines Steins überbrücken.

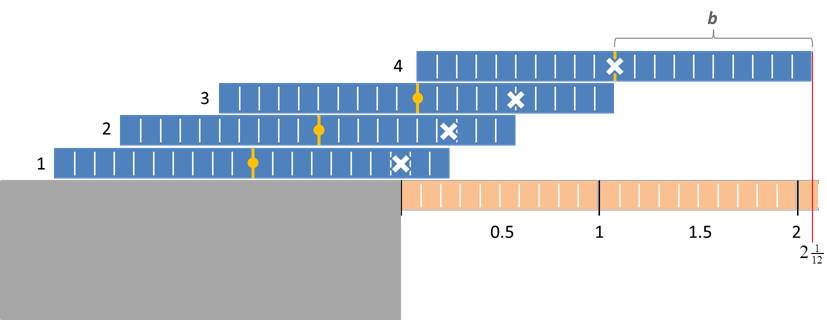
Abbildung 3

Zur Untersuchung des allgemeinen Falls schauen wir uns die Beziehungen zwischen der Lage der Steine und den resultierenden Schwerpunkten genauer an. Dazu definieren wir $s_{nk}$ als die relative Position des Schwerpunkts der Steine $n-k+1$ bis $n$ bezogen auf den rechten Rand des darunter liegenden $n-k$ -ten Steins. In Abbildung 4 sind die Zusammenhänge dargestellt. Die weißen Kreuze markieren jeweils die Positionen der betreffenden Schwerpunkte. Liegt ein Kreuz in diesem Sinne links vom rechten Rand des $n-k$ -ten Steins, dann ist $s_{nk}$ negativ, liegt es rechts davon, dann ist der Wert positiv, wobei letzteres natürlich bedeutet, dass der Stapel einstürzt.

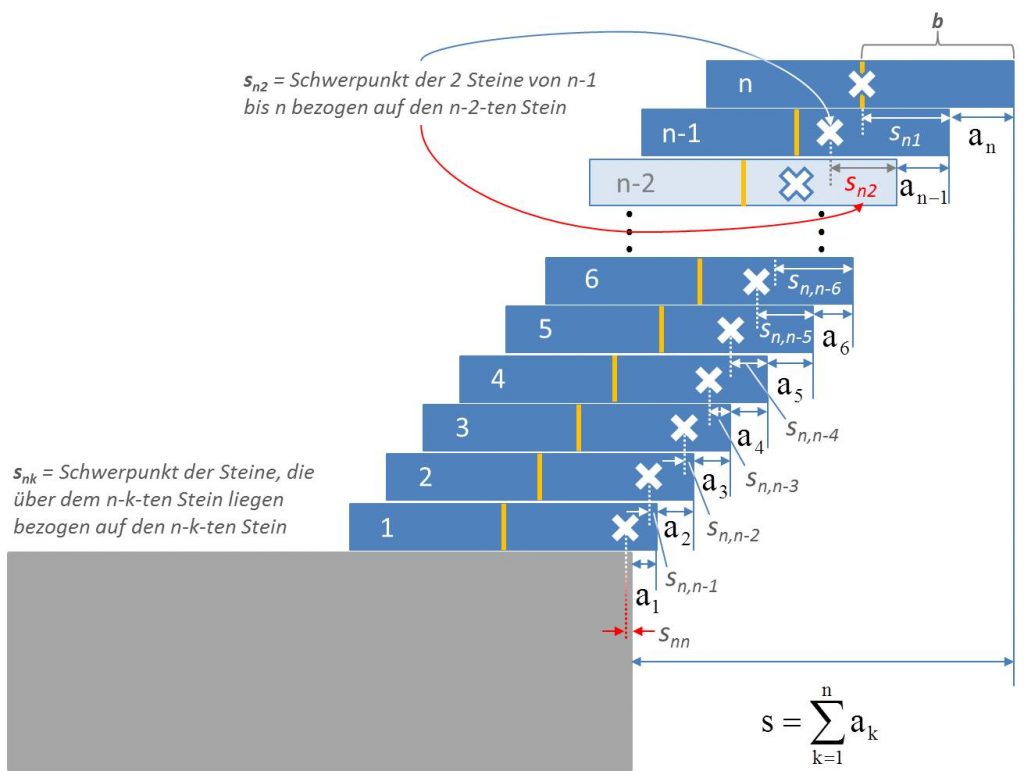
Abbildung 4

Beispiele:

$s_{n1} =a_n - b$ ist der Schwerpunkt des $n$ -ten Steins bezogen auf den $n-1$ -ten Stein.

$s_{n2} = \dfrac{a_{n-1}-b + \left(s_{n1}+a_{n-1}\right)}{2}$ ist der gemeinsame Schwerpunkt des $n-1$ -ten und des $n$ -ten Steins bezogen auf den $n-2$ -ten Stein.

$s_{n3} = \dfrac{a_{n-2}-b + \left(s_{n2}+a_{n-2}\right)\cdot 2}{3}$ ist der gemeinsame Schwerpunkt des $n-2$ -ten, $n-1$ -ten und des $n$ -ten Steins bezogen auf den $n-3$ -ten Stein. Der Faktor 2 steht hier im Zähler hinter der Klammer, weil der Ausdruck $s_{n2}+a_{n-2}$ die Lage des Schwerpunkts von $2$ Steinen repräsentiert (nämlich die über Stein Nummer $n-2$ liegenden Steine mit den Nummern $n-1$ und $n$ ).

Nur der Vollständigkeit halber: $s_{n0} = -b$ ist in dieser Terminologie der Schwerpunkt des $n$ -ten Steins bezogen auf den $n$ -ten Stein.

Allgemein gilt für die Berechnung des Schwerpunkts der Steine $n-k+1$ bis $n$ bezogen auf den darunter liegenden $n-k$ -ten Stein:

(1) $\begin{equation*} s_{nk} = \dfrac{a_{n-k+1}-b + \left(s_{n,k-1}+a_{n-k+1}\right)\cdot (k-1)}{k}\end{equation*}$

Wann können wir sicher sein, dass der Stapel nicht stürzt? Ganz einfach: Der Stapel ist stabil, wenn für alle Steine gilt, dass der Schwerpunkt des über einem gegebenen Steins gestapelten Turms innerhalb der Begrenzungen des jeweiligen Steins liegt. Nach den gewählten Bezeichnungen können wir dieses Kriterium formal so schreiben:

(2) $\begin{equation*} s_{nk} < 0 \quad \text{für alle } k, \, 1\le k \le n \end{equation*}$

Damit wird ein System von $n$ Ungleichungen definiert. Wie schon oben gesehen, gilt $s_{n1} =a_n - b$ . Demnach erhalten wir mittels Formel (1)

(3) $\begin{equation*} \begin{split} s_{n2} &< \dfrac{a_{n-1}-b + \left(s_{n1}+a_{n-1}\right)\cdot 1}{2} \\ &= \dfrac{a_{n-1}-b + \left(a_n - b + a_{n-1}\right)}{2} \\ &= \dfrac{a_n + 2a_{n-1}}{2} - b \end{split} \end{equation*}$

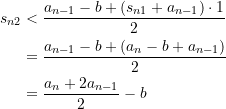
und somit weiter sukzessive

(4) $\begin{equation*} \begin{split} s_{n2} &< \dfrac{1}{2} \left( a_{n} + 2 a_{n-1}\right) - b \\ s_{n3} &< \dfrac{1}{3} \left( a_{n} + 2 a_{n-1} + 3 a_{n-2}\right) - b \\ s_{n4} &< \dfrac{1}{4} \left( a_{n} + 2 a_{n-1} + 3 a_{n-2} + 4 a_{n-3}\right) - b \\ &\vdots \\ s_{nn} &< \dfrac{1}{n} \left( a_{n} + 2 a_{n-1} + 3 a_{n-2} + 4 a_{n-3} + \cdots + n a_{1}\right) - b \end{split} \end{equation*}$

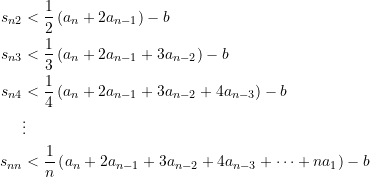
Demnach lautet die Formel für die direkte Bestimmung der Schwerpunkte $s_{nk}$

(5) $\begin{equation*} s_{nk} = -b + \dfrac{1}{k} \sum\limits_{j=1}^{k} {ja_{n-j+1}} \end{equation*}$

Die obige Bedingung dafür, dass die gestapelten Steine nicht stürzen, lässt sich nun explizit in der Form

(6) $\begin{equation*} \sum\limits_{j=1}^{k} {ja_{n-j+1}} < k\cdot b \quad \text{für alle } k, \, 1\le k \le n \end{equation*}$

niederschreiben. Übersichtlicher ist die Matrixschreibweise:

(7) $\begin{equation*} \begin{pmatrix} 1 &0 &0 &\cdots &0 &0 \\ 1 &2 &0 &\cdots &0 &0 \\ 1 &2 &3 &\cdots &0 &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\ 1 &2 &3 &\cdots &{n-1} &0 \\ 1 &2 &3 &\cdots &{n-1} &n \end{pmatrix} \begin{pmatrix} a_{n} \\ a_{n-1} \\ a_{n-2} \\ \vdots \\ a_{2} \\ a_{1} \end{pmatrix} < \begin{pmatrix} 1 \\ 2 \\ 3 \\ \vdots \\ {n-1} \\ n \end{pmatrix} b \end{equation*}$

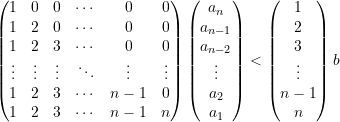
Durch Inversion der Matrix folgt daraus zunächst

(8) $\begin{equation*} \begin{pmatrix} a_{n} \\ a_{n-1} \\ a_{n-2} \\ \vdots \\ a_{2} \\ a_{1} \end{pmatrix} < \begin{pmatrix} 1 &0 &0 &\cdots &0 &0 \\ -\frac{1}{2} &\frac{1}{2} &0 &\cdots &0 &0 \\ 0 &-\frac{1}{3} &\frac{1}{3} &\cdots &0 &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\ 0 &0 &0 &\cdots &\frac{1}{n-1} &0 \\ 0 &0 &0 &\cdots &-\frac{1}{n} &\frac{1}{n} \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \\ \vdots \\ {n-1} \\ n \end{pmatrix} b \end{equation*}$

woraus wir direkt die Folgerung

(9) $\begin{equation*} \begin{split} a_{n} &< 1\cdot b \\ a_{n-1} &< \left(-\dfrac{1}{2} + 1\right) \cdot b \\ a_{n-2} &< \left(-\dfrac{2}{3} + 1\right) \cdot b \\ &\vdots \\ a_{2} &< \left(-\dfrac{n-2}{n-1} + 1\right) \cdot b\\ a_{1} &< \left(-\dfrac{n-1}{n} + 1\right) \cdot b \end{split} \end{equation*}$

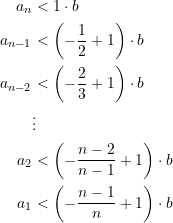
oder kürzer

(10) $\begin{equation*} \begin{split} a_{n} &< \dfrac{b}{1} \\ a_{n-1} &< \dfrac{b}{2} \\ a_{n-2} &< \dfrac{b}{3} \\ &\vdots \\ a_{2} &< \dfrac{b}{n-1} \\ a_{1} &< \dfrac{b}{n} \end{split} \end{equation*}$

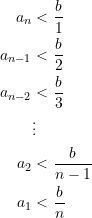
ableiten können. Insgesamt bekommen wir die notwendige und zugleich hinreichende Bedingung für einen stabilen Brückenbau einfach zu

(11) $\begin{equation*} a_{n-k+1} < \dfrac{b}{k} \quad \text{für alle } k, \, 1\le k \le n \end{equation*}$

bzw.

(12) $\begin{equation*} a_{k} < \frac{b}{n-k+1} \quad \text{für alle } k, \, 1\le k \le n \end{equation*}$

Nun können wir die aufgeworfene Frage zu dem maximal erreichbaren Wert für die Spannweite $s$ der Brücke beantworten. Bei einer gegebenen Anzahl von Steinen gilt

(13) $\begin{equation*} s = s(n) < b \cdot H_n = b \cdot \sum\limits_{k=1}^{n} {\frac{1}{k}} \end{equation*}$

Hierbei steht $H_n$ für die $n$ -te harmonische Zahl. Wenn wir die $a_k$ hinreichend nahe an $\dfrac{b}{n-k+1}$ wählen, dann können wir mit einer vorgegebenen Anzahl von Steinen den Stapel stets so bauen, dass damit die Spannweite $b \cdot H_n$ nahezu erreicht wird und der Stapel trotzdem stabil bleibt. Da nun aber $H_n$ für $n \rightarrow \infty$ über alle Grenzen wächst, können wir bei einer unbegrenzten Anzahl von Steinen jeden beliebig großen Überhang $s$ konstruieren.

Somit schaffen wir es, den Stapel beliebig weit über die Tischkante hinaus zu bauen. Abbildung 5 zeigt ein Beispiel mit 11 Steinen und dem damit erreichten Überhang von $s = 3.019\overline{877344}$

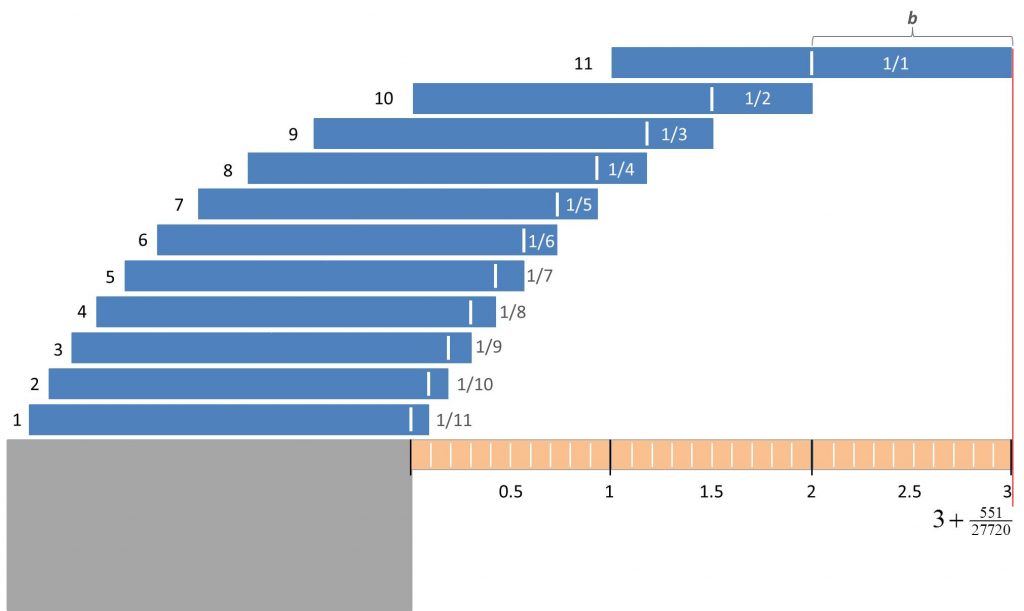
Abbildung 5

Das „harmonische“ Konstruktionsprinzip ist einfach: Bei $n$ Steinen schiebt man den ersten Stein knapp um die Länge $\dfrac{b}{n}$ über die Tischkante hinaus, den zweiten dann knapp um die Länge $\dfrac{b}{n-1}$ über den ersten Stein, usw. bis zum $n-1$ -ten Stein, der dann um fast $\dfrac{b}{2}$ über den $n-2$ -ten Stein hinausragen darf und schließlich zum $n$ -ten Stein, der knapp um die Länge $b$ über den $n-1$ -ten Stein hinauszeigt. In Abbildung 5 ist dies für 11 Steine detailliert ausgeführt.

Wir hatten oben erwähnt, dass $H_n$ über alle Grenzen wächst, dass also $lim_{n\rightarrow \infty} H_n = \infty$ gilt. Dass dies tatsächlich so ist, sieht man ganz leicht. Für $n > 1$ haben wir

$\begin{equation*} \begin{split} H_{2^n} &= \sum\limits_{k=1}^{2^n} {\dfrac{1}{k}} \\ &= 1 + \dfrac{1}{2}+ \dfrac{1}{3}+ \dfrac{1}{4} + \dfrac{1}{5}+ \dfrac{1}{6} + \dfrac{1}{7} + \dfrac{1}{8} + \dfrac{1}{9} + \dfrac{1}{10} + \dfrac{1}{11} + \dfrac{1}{12}+\cdots \\ &= 1 + \dfrac{1}{2}+ \left(\dfrac{1}{3}+ \dfrac{1}{4}\right) + \left(\dfrac{1}{5}+ \dfrac{1}{6}+ \dfrac{1}{7}+ \dfrac{1}{8}\right) \\ &\quad +\left(\dfrac{1}{9} + \dfrac{1}{10}+ \dfrac{1}{11}+ \dfrac{1}{12} + \cdots + \dfrac{1}{16} \right) + \cdots \end{split} \end{equation*}$

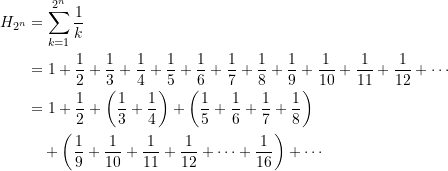
und weiter

(14) $\begin{equation*} \begin{split} H_{2^n} &> 1 + \dfrac{1}{2}+ 2\cdot\dfrac{1}{4} + 4\cdot\dfrac{1}{8} + 8\cdot\dfrac{1}{16} + \cdots \\ &= 1 + \underset{n\times \frac{1}{2}}{\left(\dfrac{1}{2} + \dfrac{1}{2} + \dfrac{1}{2} + \dfrac{1}{2} + \cdots \right)}\\ &= 1 +\dfrac{n}{2} \end{split} \end{equation*}$

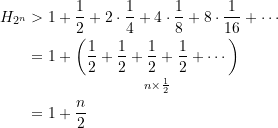
Somit gilt für $n > 2$

(15) $\begin{equation*} H_n > 1 +\dfrac{\lfloor {\log_2(n)} \rfloor}{2} \end{equation*}$

Beispiel 1a: Um eine Brücke der Länge $10b$ zu bauen, brauchen wir also nicht mehr als $2^{18}=262144$ Steine der Länge $2b$ , denn $H_{2^{18}} > 1 +\dfrac{\lfloor {\log_2(2^{18})} \rfloor}{2} = 10$ .

Umgekehrt kann man auch nach einer einfachen Schätzformel für die Mindestanzahl der Steine fragen die nötig ist, um eine gewünschte Strecke zu überbrücken. In obiger Ableitung haben wir für $n \ge 1$

$\begin{equation*} \begin{split} H_{2^n} &= \sum\limits_{k=1}^{2^n} {\dfrac{1}{k}} \\ &= 1 + \dfrac{1}{2}+ \left(\dfrac{1}{3}+ \dfrac{1}{4}\right) + \left(\dfrac{1}{5}+ \dfrac{1}{6}+ \dfrac{1}{7}+ \dfrac{1}{8}\right) \\ &\quad +\left(\dfrac{1}{9} + \dfrac{1}{10}+ \dfrac{1}{11}+ \dfrac{1}{12} + \cdots + \dfrac{1}{16} \right) + \cdots \end{split} \end{equation*}$

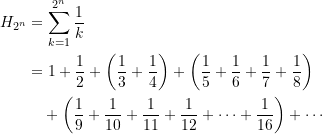
woraus folgt

(16) $\begin{equation*} \begin{split} H_{2^n} &< 1 + 2\cdot\dfrac{1}{2}+ 2\cdot\dfrac{1}{2} + 4\cdot\dfrac{1}{4} + 8\cdot\dfrac{1}{8} + \cdots \\ &= 1 + \underset{n\times 1}{\left(1 + 1 + 1 + 1 + \cdots \right) }\\ &= 1 + n \end{split} \end{equation*}$

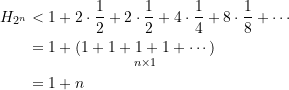
Insgesamt bekommen wir daher die Abschätzung

(17) $\begin{equation*} 1 + \dfrac{\lfloor {\log_2(n)} \rfloor}{2} < H_n < 1 + \lceil {\log_2(n)} \rceil \end{equation*}$

wobei die linke Seite für $n > 2$ und die rechte Seite für $n \ge 2$ gilt.

Beispiel 1b: Um eine Strecke der Länge $20b$ zu überbrücken werden mindestens $2^{19}=524288$ Steine der Länge $2b$ benötigt, denn $H_{2^{19}} < 1 +\lceil {\log_2(2^{19})} \rceil = 20$ .

Die so erhaltenen Abschätzungen sind ziemlich ungenau, das geht natürlich besser. Eine sehr gute Approximation ist gegeben durch die folgende Ungleichung

(18) $\begin{equation*} \gamma + \log\left(n+\frac{1}{2}\right) < H_n < \gamma + \log\left(n+\frac{1}{2}\right) + \frac{1}{24\,n^2} \end{equation*}$

Dabei ist $\gamma = 0.577215664901532860606512090\dots$ die Eulersche Gamma-Konstante, auch Euler-Mascheroni-Konstante genannt. Diese Konstante ergibt sich aus der Überlegung

(19) $\begin{equation*} \sum\limits_{k=1}^{n} {\dfrac{1}{k}} \approx \int\limits_{1}^{n} {\dfrac{1}{x} \:\mathrm{d}x} \end{equation*}$

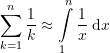
woraus bei genauerer Analyse und der Ersetzung $\int\limits_{1}^{n} {\dfrac{1}{x} \:\mathrm{d}x} = \log(n)$ schon Euler

(20) $\begin{equation*} \sum\limits_{k=1}^{n} {\dfrac{1}{k}} = \log(n) \; + \text{const.} \; + O\left({\dfrac{1}{n}}\right) \quad \text{für } n \rightarrow \infty \end{equation*}$

gefolgert und mit der Definition $\gamma = \text{const.}$ den Grenzwert

(21) $\begin{equation*} \lim_{n \rightarrow \infty } \left(H_n - \log(n)\right) = \gamma \end{equation*}$

erhalten hat. Umgekehrt können wir so $n$ näherungsweise aus $m=H_n$ bestimmen.

(22) $\begin{equation*} n \approx \lfloor {e^{m - \gamma} + \frac{1}{2}}\rfloor \end{equation*}$

Damit erhalten wir für die beiden obigen Beispiele viel bessere Abschätzungen:

Beispiel 2a: Um eine Brücke der Länge $10b$ zu bauen, brauchen wir also nicht mehr als $\lfloor {e^{10 - \gamma} + \frac{1}{2}}\rfloor = 12367$ Steine der Länge $2b$ , denn $H_{12367} > \gamma + \log\left(12367+\frac{1}{2}\right) \approx 10$ .

Beispiel 2b: Um eine Strecke der Länge $20b$ zu überbrücken werden mindestens $\lfloor {e^{20 - \gamma} + \frac{1}{2}}\rfloor = 272400600$ Steine der Länge $2b$ benötigt, denn $H_{272400600} < \gamma + \log\left(272400600+\frac{1}{2}\right) + \frac{1}{24\,n^2} \approx 20$ .

In The On-Line Encyclopedia of Integer Sequences: https://oeis.org/A002387 (Harmonic numbers: Least n such that H(n) > m, where H(n) is the harmonic number sum_{k=1..n} 1/k) findet man eine Tabelle, die zu vorgegebenen Werten $m$ den minimalen Wert $n$ angibt, für den $H_n > m$ gilt.

In unserer Terminologie finden wir also damit zu vorgegebenen Brückenspannweiten von $m\cdot b$ die gerade ausreichende Anzahl von Steinen $n$ , für die $H_n$ erstmals den Wert $m$ überschreitet, womit die konstruierte Brücke sodann die Strecke $s = m\cdot b$ überspannt.

Die genauen Werte für die nötige Anzahl der Steine zur Überbrückung einer Strecke von $m\cdot b$ kann man für $m = 1\cdots 30$ der folgenden Tabelle entnehmen (s. OEIS, https://oeis.org/A002387).

$m$	minimales $n$ , so dass $H_n > m$	$m$	minimales $n$ , so dass $H_n > m$	$m$	minimales $n$ , so dass $H_n > m$
1	2	11	33617	21	740461601
2	4	12	91380	22	2012783315
3	11	13	248397	23	5471312310
4	31	14	675214	24	14872568831
5	83	15	1835421	25	40427833596
6	227	16	4989191	26	109894245429
7	616	17	13562027	27	298723530401
8	1674	18	36865412	28	812014744422
9	4550	19	100210581	29	2207284924203
10	12367	20	272400600	30	6000022499693

Wie man sieht: Wirklich große Spannweiten kann man so in der Praxis nicht überbrücken. Für einen Überhang von $1000\cdot b$ braucht man nach obiger Schätzformel etwa $\lfloor {e^{1000 - \gamma} + \frac{1}{2}}\rfloor \approx 1.1061151102660\cdot 10^{434}$ Steine – das sind deutlich mehr als die ca. $10^{80}$ Atome im Universum.

Harmonische Brücken

Schreibe einen Kommentar Antwort abbrechen