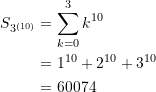Die Anzahl der Quadrate in einem Rechteck mit den Seitenlängen ![]() , wobei
, wobei ![]() und
und ![]() kann man leicht abzählen. In der nachfolgenden Grafik ist ein Beispiel mit
kann man leicht abzählen. In der nachfolgenden Grafik ist ein Beispiel mit ![]() Feldern dargestellt. Es gibt offensichtlich
Feldern dargestellt. Es gibt offensichtlich ![]() Quadrate mit der Seitenlänge 1,
Quadrate mit der Seitenlänge 1, ![]() Quadrate mit der Seitenlänge 2,
Quadrate mit der Seitenlänge 2, ![]() Quadrate mit der Seitenlänge 3, usw. … bis
Quadrate mit der Seitenlänge 3, usw. … bis ![]() Quadrate mit der Seitenlänge 6. In der Grafik sind einige der so entstehenden Quadrate exemplarisch eingezeichnet (gestrichelt und in Farbe).
Quadrate mit der Seitenlänge 6. In der Grafik sind einige der so entstehenden Quadrate exemplarisch eingezeichnet (gestrichelt und in Farbe).
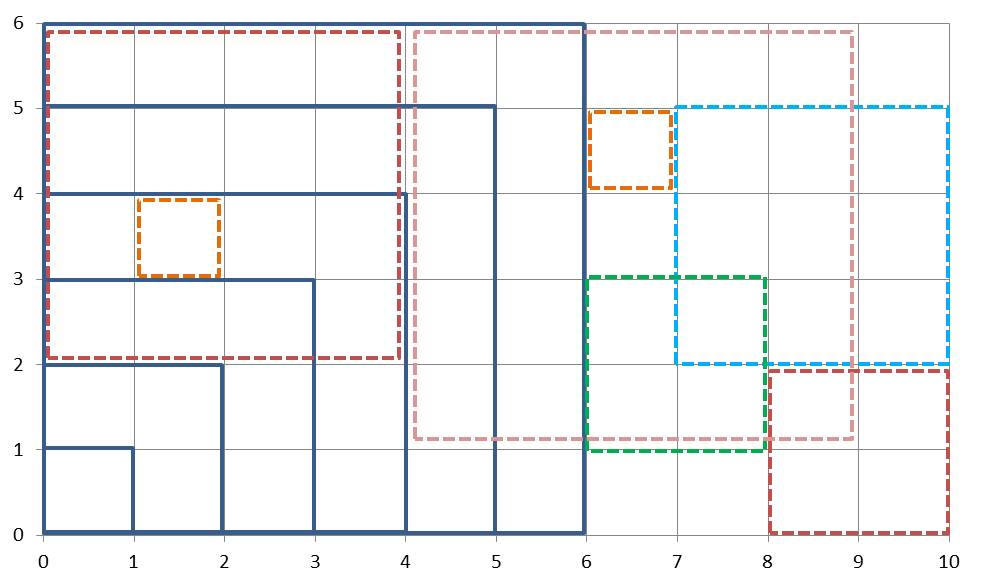
Abbildung 1
In Summe sind es hier ![]() Quadrate. Die allgemeine Formel für die Summe der Quadrate in einem Rechteck mit den Seitenlängen
Quadrate. Die allgemeine Formel für die Summe der Quadrate in einem Rechteck mit den Seitenlängen ![]() mit und
mit und ![]() lautet
lautet
(1) 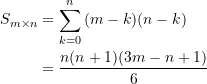
Die Anzahl der Quadrate in einem Quadrat mit den Seitenlängen ![]() , mit
, mit ![]() ist
ist
(2) 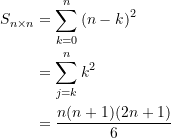
In Abbildung 2 ist ein Beispiel mit ![]() Feldern dargestellt.
Feldern dargestellt.
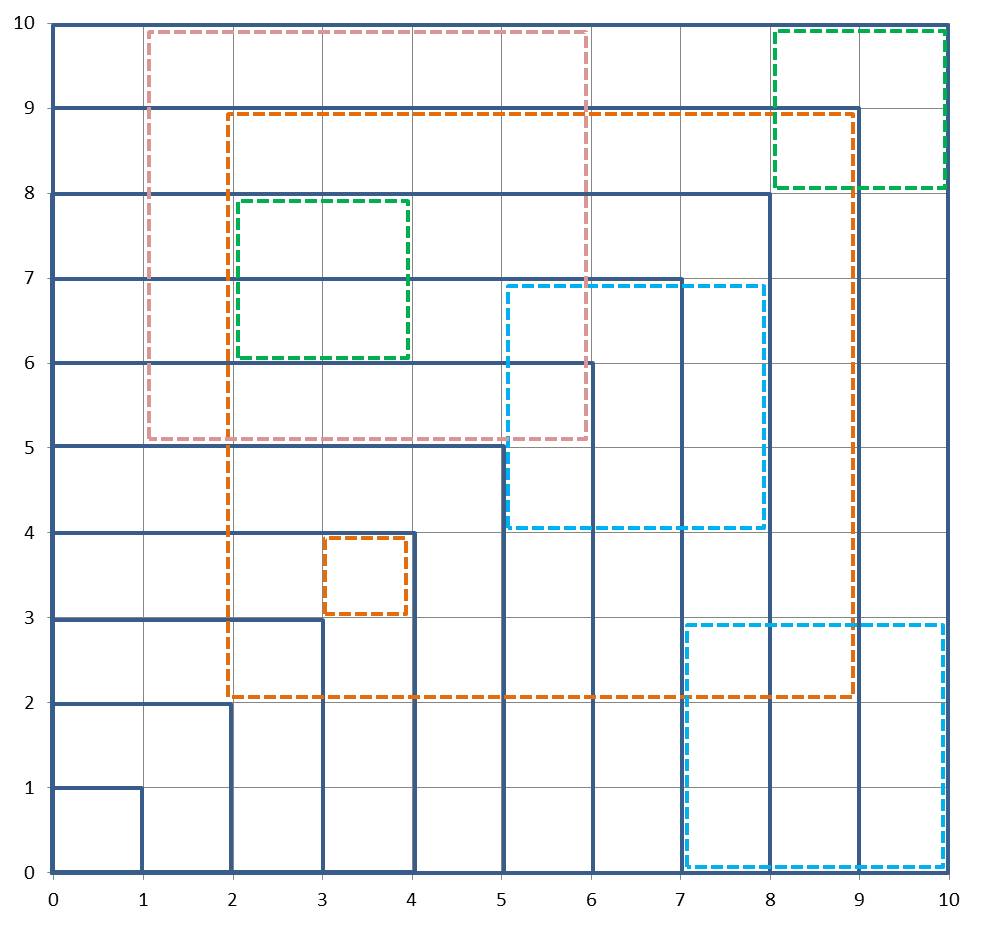
Abbildung 2
Hier erhalten wir jetzt nach obiger Formel insgesamt bereits ![]() Quadrate.
Quadrate.
Die Entsprechung zum Quadrat in der dritten Dimension ist der Würfel. Man kann also genau so fragen, wie viele Würfel in einem Quader mit den Seitenlängen ![]() enthalten sind. Setzen wir
enthalten sind. Setzen wir ![]() , so erhalten wir für die Summe der Würfel
, so erhalten wir für die Summe der Würfel
(3) ![]()
Ein Quader mit den Seitenlängen ![]() enthält somit
enthält somit
(4) 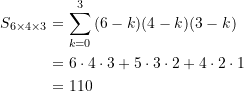
Würfel (s. Abbildung 3)
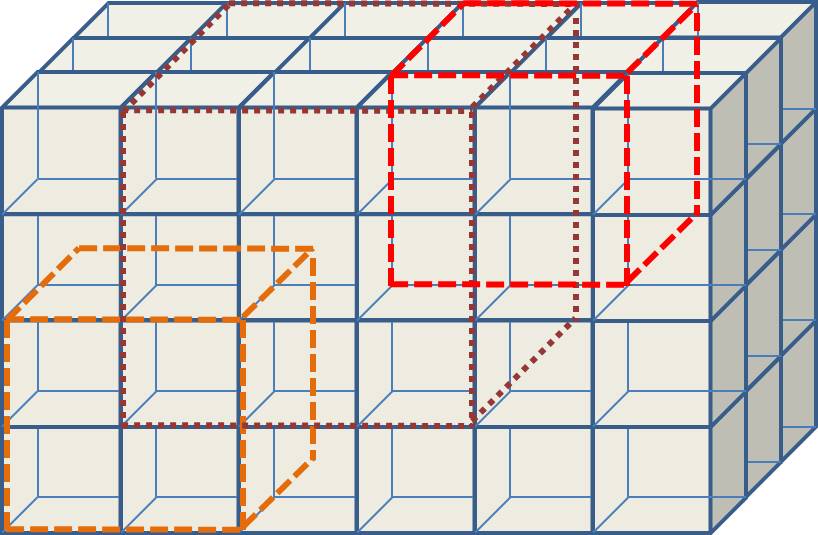
Abbildung 3
Die geschlossene Formel hierfür lautet
(5) ![]()
Dabei haben wir ohne Beschränkung der Allgemeinheit ![]() als den kleinsten Wert unter den drei Dimensionsparametern
als den kleinsten Wert unter den drei Dimensionsparametern ![]() und
und ![]() angenommen. Das obige Rechenbeispiel wird jetzt zu
angenommen. Das obige Rechenbeispiel wird jetzt zu
(6) 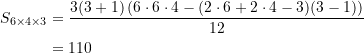
Wenn alle Seitenlängen gleich sind, also ![]() gilt, vereinfacht sich die Formel auf
gilt, vereinfacht sich die Formel auf
(7) ![]()
Wie man damit leicht berechnet, sind somit in einem 3-dimensionalen Quader mit den gleichen Seitenlängen ![]() insgesamt
insgesamt
(8) 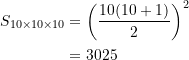
Würfel mit den Seitenlängen ![]() enthalten.
enthalten.
In ![]() Dimensionen gilt eine zu (1) und (3) analoge Formel. Nehmen wir einen
Dimensionen gilt eine zu (1) und (3) analoge Formel. Nehmen wir einen ![]() -dimensionalen Quader mit den Seitenlängen
-dimensionalen Quader mit den Seitenlängen ![]() , wobei
, wobei ![]() ,
, ![]() ,
, ![]() und
und ![]() . Wir erhalten die folgende Formel
. Wir erhalten die folgende Formel
(9) ![]()
Sind auch hier wieder alle Seitenlängen gleich, also ![]() für
für ![]() und somit
und somit ![]() , so ergibt sich die Vereinfachung
, so ergibt sich die Vereinfachung
(10) 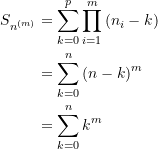
(s. entsprechende Summenformeln für ![]() )
)
Zwei Beispiele auch hierzu:
Dimension ![]() , Seitenlängen
, Seitenlängen ![]() :
:
(11) 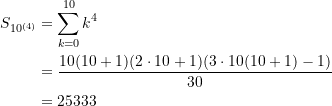
Dimension ![]() , Seitenlängen
, Seitenlängen ![]() :
:
(12)