- Die Originalvariante
- Diskussion zur Originalvariante
- Abwandlungen zum Geschwisterproblem
- Verallgemeinerungen zur Originalvariante
1 Das Geschwisterparadoxon 
1.1 Die Originalvariante
Das Paradoxon lautet:
- (1) Eine Familie habe zwei Kinder. Eines davon ist ein Mädchen. Mit welcher Wahrscheinlichkeit ist auch das zweite Kind ein Mädchen?
Das Rätsel ist gleichfalls bekannt unter dem Namen „Geschwisterproblem“. Allgemein wird die gestellte Frage mit ![]() beantwortet. Vereinzelt wird allerdings die Auffassung vertreten, die Wahrscheinlichkeit sei
beantwortet. Vereinzelt wird allerdings die Auffassung vertreten, die Wahrscheinlichkeit sei ![]() und nicht
und nicht ![]() . Im Folgenden werden die diesbezüglichen Argumente als nicht stichhaltig entkräftet. Das zweite Kind ist also unter den gegebenen Bedingungen mit der Wahrscheinlichkeit
. Im Folgenden werden die diesbezüglichen Argumente als nicht stichhaltig entkräftet. Das zweite Kind ist also unter den gegebenen Bedingungen mit der Wahrscheinlichkeit ![]() ein Mädchen.
ein Mädchen.
Versuchen wir, das Problem ganz formal zu behandeln und betrachten wir daher den Ereignisraum. Durch den ersten Satz wird zunächst die überhaupt interessierende Grundgesamtheit auf die Menge
(1) ![]()
festgelegt (![]() = Junge,
= Junge, ![]() = Mädchen). Diese Information ist natürlich wichtig, es könnten ja auch 5 Kinder oder 3 Kinder und 2 Fahrräder gemeint sein. In tabellarischer Form ist dies die Grundgesamtheit:
= Mädchen). Diese Information ist natürlich wichtig, es könnten ja auch 5 Kinder oder 3 Kinder und 2 Fahrräder gemeint sein. In tabellarischer Form ist dies die Grundgesamtheit:
| 1 | |
| 2 | |
| 3 | |
| 4 |
Tabelle 1‑1
Der zweite Satz macht nun eine einschränkende Aussage über die Grundgesamtheit: nicht die Menge ![]() ist gemeint, sondern die kleinere Grundgesamtheit
ist gemeint, sondern die kleinere Grundgesamtheit
(2) ![]()
also die Menge ![]() ohne das Paar
ohne das Paar ![]() [die Zeilen 2, 3 und 4 in der Tabelle].
[die Zeilen 2, 3 und 4 in der Tabelle].
Mit diesen beiden Sätzen ist die relevante Grundgesamtheit endgültig auf ![]() festgelegt. Es macht im Folgenden also keinen Sinn mehr, auf die prinzipiell mögliche Kombination
festgelegt. Es macht im Folgenden also keinen Sinn mehr, auf die prinzipiell mögliche Kombination ![]() zu verweisen. Dieser Ausgang des „Experiments“ ist voraussetzungsgemäß nach den Rahmenbedingungen unter denen die Frage nach der Wahrscheinlichkeit gestellt wird definitiv ausgeschlossen. Das Ereignis
zu verweisen. Dieser Ausgang des „Experiments“ ist voraussetzungsgemäß nach den Rahmenbedingungen unter denen die Frage nach der Wahrscheinlichkeit gestellt wird definitiv ausgeschlossen. Das Ereignis ![]() ist somit nicht Teil der relevanten Grundgesamtheit, daher kann es unter den gegebenen Bedingungen auch nicht eintreten bzw. ist als nicht eingetreten ausgeschlossen und interessiert folglich nicht. Genauso wenig, wie eine Familie mit genau zwei Kindern nun einmal keine drei Kinder hat (will sagen, keines der Ereignisse
ist somit nicht Teil der relevanten Grundgesamtheit, daher kann es unter den gegebenen Bedingungen auch nicht eintreten bzw. ist als nicht eingetreten ausgeschlossen und interessiert folglich nicht. Genauso wenig, wie eine Familie mit genau zwei Kindern nun einmal keine drei Kinder hat (will sagen, keines der Ereignisse ![]() kann eintreten) aber auch nicht nur ein Kind hat (keines der Ereignisse
kann eintreten) aber auch nicht nur ein Kind hat (keines der Ereignisse ![]() oder
oder ![]() ist im Kontext erlaubt).
ist im Kontext erlaubt).
In diesem Zusammenhang sollte klar werden, dass auch der Satz „Eine Familie habe zwei Kinder“ nicht anderes ist, als eine einschränkende Aussage über die erlaubte Grundgesamtheit. Die weitere Enthüllung: „Eines davon sei ein Mädchen“ steht in diesem Sinne mathematisch gesehen gleichrangig daneben, auch wenn, rein sprachlogisch, dem ersten Satz des Rätsels scheinbar ein höheres Gewicht zukommt. Erst zusammengenommen ist die relevante Grundgesamtheit definiert. Der verschiedentlich gehörte Einwand, Einschränkungen oder zusätzliche Informationen könnten nur nach dem Ziehen gemacht werden trägt dieser definitorischen Bestimmung des Ereignisraums nicht Rechnung.
Nachdem also ![]() die relevante Grundgesamtheit ist und allen drei möglichen Ereignissen darin die gleiche Wahrscheinlichkeit zukommt, ist die Wahrscheinlichkeit dafür, dass auch das zweite Kind ein Mädchen ist
die relevante Grundgesamtheit ist und allen drei möglichen Ereignissen darin die gleiche Wahrscheinlichkeit zukommt, ist die Wahrscheinlichkeit dafür, dass auch das zweite Kind ein Mädchen ist ![]() und nicht
und nicht ![]() wie man intuitiv erwartet.
wie man intuitiv erwartet.
Beleuchten wir noch die eigentliche Frage: „Mit welcher Wahrscheinlichkeit ist auch das andere Kind ein Mädchen?“. Im Kontext der Voraussetzung „es gibt ein Mädchen“ ist das mathematisch äquivalent zu der Formulierung „mit welcher Wahrscheinlichkeit sind dann beide Kinder Mädchen?“.
An dieser Stelle sei darauf verwiesen, dass der Befund (![]() dafür, dass auch das zweite Kind ein Mädchen ist) sich gleichfalls auch dann ergibt, wenn die Grundgesamtheit auf
dafür, dass auch das zweite Kind ein Mädchen ist) sich gleichfalls auch dann ergibt, wenn die Grundgesamtheit auf ![]() festgelegt wird und die weitere Information „eines davon ist ein Mädchen“ als Zusatzinformation „nach der Ziehung“ gegeben wird. Die Frage nach der Wahrscheinlichkeit für das Ereignis
festgelegt wird und die weitere Information „eines davon ist ein Mädchen“ als Zusatzinformation „nach der Ziehung“ gegeben wird. Die Frage nach der Wahrscheinlichkeit für das Ereignis ![]() , „das andere Kind ist ein Mädchen“ bezieht sich nun darauf, dass das Ereignis
, „das andere Kind ist ein Mädchen“ bezieht sich nun darauf, dass das Ereignis ![]() „eines davon ist ein Mädchen“ eingetreten ist. Es wird hier also nach einer bedingten Wahrscheinlichkeit gefragt. Bezeichnen wir
„eines davon ist ein Mädchen“ eingetreten ist. Es wird hier also nach einer bedingten Wahrscheinlichkeit gefragt. Bezeichnen wir ![]() als das Ereignis, dass bei zufälliger Wahl zweier Kinder beide Kinder Mädchen sind, so ist also
als das Ereignis, dass bei zufälliger Wahl zweier Kinder beide Kinder Mädchen sind, so ist also ![]() nichts anderes, als das bedingte Ereignis «
nichts anderes, als das bedingte Ereignis «![]() unter der Bedingung
unter der Bedingung ![]() » (
» (![]() ). Formelmäßig haben wir daher
). Formelmäßig haben wir daher
(3) ![]()
Die Wahrscheinlichkeit ![]() ist
ist ![]() (drei der vier Paare aus
(drei der vier Paare aus ![]() enthalten ein
enthalten ein ![]() ), die Wahrscheinlichkeit
), die Wahrscheinlichkeit ![]() ist
ist ![]() (nur eines der vier Paare aus
(nur eines der vier Paare aus ![]() enthält zwei
enthält zwei ![]() ). Daher gilt
). Daher gilt ![]() .
.
Wer nun aber der Auffassung ist, die Wahrscheinlichkeit für das Eintreten von ![]() sei nun einmal
sei nun einmal ![]() , weil die Fälle
, weil die Fälle ![]() und
und ![]() gleichwahrscheinlich sind, übersieht dabei, dass
gleichwahrscheinlich sind, übersieht dabei, dass ![]() kein „absolutes“ sondern ein bedingtes Ereignis darstellt. Aus der Annahme
kein „absolutes“ sondern ein bedingtes Ereignis darstellt. Aus der Annahme ![]() folgt deshalb nach den Rechenregeln für bedingte Wahrscheinlichkeiten der Widerspruch
folgt deshalb nach den Rechenregeln für bedingte Wahrscheinlichkeiten der Widerspruch
(4) ![]()
1.2 Diskussion zur Originalvariante
Um noch klarer herauszuarbeiten, wie man zu dem richtigen Ergebnis ![]() gelangt, schauen wir uns die bestimmenden Überlegungen im Detail an und diskutieren dazu die folgende Variante:
gelangt, schauen wir uns die bestimmenden Überlegungen im Detail an und diskutieren dazu die folgende Variante:
- (2) Eine Familie habe zwei Kinder. Eines davon ist ein Junge oder ein Mädchen. Mit welcher Wahrscheinlichkeit ist das andere Kind ein Mädchen? [Man beachte den Unterschied zur Variante (1)]
Natürlich gibt uns hier der Einschub („eines davon ist ein Junge oder ein Mädchen“) keinen weiteren Aufschluss zur relevanten Grundgesamtheit, das wussten wir ja schon. Im Gegensatz zum obigen Hinweis („eines davon ist ein Mädchen“) handelt es sich nur um eine bloße Scheininformation, die zudem den Leser irreführen soll. Der Einschub ist indessen nötig, um in der sich anschließenden Fragestellung auf das „andere Kind“ abheben zu können.
Des „Rätsels“ Lösung liegt auf der Hand: da wir keine weiteren Informationen zu den Kindern haben, können wir davon ausgehen, dass Jungen und Mädchen gleich häufig vorkommen. Es ist daher ohne weitere Rechnung intuitiv klar, dass das andere Kind mit 50%-iger Wahrscheinlichkeit ein Mädchen ist. Richten wir das Augenmerk trotzdem genauer auf die Frage, wie es zu dieser Antwort kommt. Dazu erweitern wir das Szenario um einen unabhängigen Beobachter. Den Beobachter bitten wir um die zufällige Auswahl eines der Kinder und um Mitteilung des Geschlechts desselben.
- (3) Eine Familie habe zwei Kinder. Wir bitten einen unabhängigen Beobachter um die zufällige Auswahl eines der Kinder und fragen ihn: Ist es ein Junge oder Mädchen? Er antwortet wahrheitsgemäß mit: „Es ist ein Junge“ bzw. „Es ist ein Mädchen“. Mit welcher Wahrscheinlichkeit ist das andere Kind ein Mädchen?
Die möglichen Ergebnisse sind in der folgenden Tabelle aufgelistet:
| Nr. | Geschlechter | Geschlecht des vom Beobachter zufällig gewählten Kindes | Geschlecht des anderen Kindes | W. für das Eintreten des Ereignisses |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
Tabelle 1‑2
Mit 50%-iger Wahrscheinlichkeit ist das von dem unabhängigen Beobachter gewählte Kind ein Junge (Zeilen 1 und 2 der Tabelle). In jeweils der Hälfte der Fälle (![]() zu
zu ![]() ) ist dabei das andere Kind ein Junge (Zeile 1) bzw. ein Mädchen (Zeile 2). Zum gleichen Ergebnis gelangt man, wenn der Beobachter ein Mädchen gewählt hat (Zeilen 3 und 4). Insgesamt ist daher, unabhängig von der Auswahl des Beobachters, das andere Kind mit der Wahrscheinlichkeit
) ist dabei das andere Kind ein Junge (Zeile 1) bzw. ein Mädchen (Zeile 2). Zum gleichen Ergebnis gelangt man, wenn der Beobachter ein Mädchen gewählt hat (Zeilen 3 und 4). Insgesamt ist daher, unabhängig von der Auswahl des Beobachters, das andere Kind mit der Wahrscheinlichkeit ![]() ein Mädchen (Zeilen 2 und 4). Die fragliche Wahrscheinlichkeit ist also tatsächlich
ein Mädchen (Zeilen 2 und 4). Die fragliche Wahrscheinlichkeit ist also tatsächlich ![]() .
.
- (4) Eine Familie habe zwei Kinder. Wir fragen einen unabhängigen Beobachter: Ist es eines der Kinder ein Mädchen? Er antwortet wahrheitsgemäß mit: „JA“ bzw. „NEIN“. Mit welcher Wahrscheinlichkeit ist das andere Kind ein Mädchen?
Nun stellen wir dem Beobachter also eine andere Frage: Ist eines der Kinder ein Mädchen? Der Beobachter teilt uns dabei nicht mit, welches Kind er ggf. fixiert. Er antwortet nur mit JA oder NEIN. Die folgende Tabelle gibt den Überblick zu den möglichen Ereignissen. Um den Zusammenhang mit dem Obigen nicht zu verlieren, erweitern wir einfach die vorige Tabelle um eine weitere Spalte:
| Nr. | Geschlechter | Geschlecht des vom Beobachter zufällig gewählten Kindes | Geschlecht des anderen Kindes | Antwort des Beobachters auf die Frage: Ist eines der Kinder ein Mädchen? | W. für das Eintreten des Ereignisses |
| 1 | Nein | ||||
| 2 | Ja | ||||
| 3 | Ja | ||||
| 4 | Ja |
Tabelle 1‑3
Der Tabelle entnimmt man, dass die Antwort des Beobachters auf die Frage: „Ist eines der Kinder ein Mädchen?“, auch dann JA lauten kann, wenn das von ihm zuvor zufällig gewählte Kind ein Junge ist (Zeile 2). Deswegen können wir nun konstatieren: in drei von vier Fällen (Zeilen 2, 3 und 4) ist eines der Kinder ein Mädchen, aber nur in einem dieser Fälle (Zeile 4) sind beide Kinder Mädchen. Die Wahrscheinlichkeit, dass beide Kinder Mädchen sind, ist unter der gegebenen Bedingung (Antwort auf die Frage ist JA) deswegen ![]() . Doch heißt dies auch, dass „das andere Kind“ mit der Wahrscheinlichkeit
. Doch heißt dies auch, dass „das andere Kind“ mit der Wahrscheinlichkeit ![]() ein Mädchen ist? Hierzu muss der Beobachter näher einbezogen und es muss präzisiert werden, was „das andere Kind“ heißt.
ein Mädchen ist? Hierzu muss der Beobachter näher einbezogen und es muss präzisiert werden, was „das andere Kind“ heißt.
Offensichtlich bezieht sich die Frage nach dem „anderen Kind“ sprachlich und logisch darauf, dass ein Kind bereits näher bezeichnet wurde. Im Kontext der Frage (Ist eines der Kinder ein Mädchen?) kann das nur das Bezugssubjekt des Beobachters sein, obgleich wir das nicht kennen. Zeile 1 ist irrelevant, da die Antwort NEIN lautet (in diesem Falle wissen wir mit Sicherheit, dass das „andere Kind“ kein Mädchen ist). Im Falle von Zeile 2 und 3 ist das Bezugssubjekt immerhin eindeutig bestimmt (das Mädchen, es gibt ja nur eines). In Zeile 4 gibt es indessen zwei Möglichkeiten für die Bezugnahme des Beobachters: in beiden Fällen handelt es sich um ein Mädchen, aber eben um zwei verschiedene Mädchen. Lautet die Antwort des Beobachter JA, so wissen wir nicht, welcher der Fälle 2, 3 oder 4 vorliegt. Wir wissen aber: in zwei von drei Fällen (die Zeilen 2 und 3), in denen der Beobachter mit JA antwortet, ist das „andere Kind“ ein Junge. Im verbleibenden Fall indes ist das „andere Kind“ ein Mädchen. Der Beobachter hat dabei offensichtlich zwei Möglichkeiten, ein Mädchen auszuwählen. Die Frage ist, ob durch diese zweifache Auswahlchance die Eintrittswahrscheinlichkeit für das der Zeile 4 entsprechende Ereignis verändert wird bzw. wie dieser Umstand den Ereignisraum überhaupt verändert? Betrachten wir die nochmals erweiterte Ereignistabelle:
| Nr. | Geschlechter | Geschlecht des vom Beobachter zufällig gewählten Kindes | Geschlecht des anderen Kindes | Antwort des Beobachters auf die Frage: Ist eines der Kinder ein Mädchen? | Bezugssubjekt des Beobachters | Geschlecht des anderen Kindes (bezogen auf die Wahl des Beobachters) | W. für das Eintreten des Ereignisses | |
| 1a | Nein | |||||||
| 1b | Nein | |||||||
| 2 | Ja | |||||||
| 3 | Ja | |||||||
| 4a | Ja | |||||||
| 4b | Ja |
Anmerkung: Im Falle von Zeile 1a/b bzw. 4a/b entscheidet sich der Beobachter zufällig für einen der beiden Jungen bzw. eines der Mädchen
Tabelle 1‑4
Wie man der Übersicht entnimmt, ist nun in den vier Zeilen 2, 3, 4a und 4b eines der Kinder ein Mädchen, in zweien davon (4a und 4b) ist das „andere Kind“ ein Mädchen. Bei Eintreten des Ereignisses ![]() erweist es sich indes letztlich als belanglos, welches der beiden Kinder der Beobachter als Referenz nimmt (Nr. 1 oder Nr. 2), da das „andere Kind“ hier unabhängig von der Bezugnahme des Beobachters stets ein Mädchen ist und daher durch die Wahl des Beobachters nach außen hin kein neues (unterscheidbares) Ereignis generiert wird. Ganz gleich wie sich der Beobachter entscheidet, ist im Falle des Ereignisses
erweist es sich indes letztlich als belanglos, welches der beiden Kinder der Beobachter als Referenz nimmt (Nr. 1 oder Nr. 2), da das „andere Kind“ hier unabhängig von der Bezugnahme des Beobachters stets ein Mädchen ist und daher durch die Wahl des Beobachters nach außen hin kein neues (unterscheidbares) Ereignis generiert wird. Ganz gleich wie sich der Beobachter entscheidet, ist im Falle des Ereignisses ![]() das „andere Kind“ mit Sicherheit ein Mädchen. Dies gilt natürlich auch dann, wenn wir, da wir die Wahl des Beobachters nicht kennen, mit dem „anderen Kind“ dasselbe meinen wie der Beobachter selbst. Das ist der entscheidende Punkt: die 25%-ige Eintrittswahrscheinlichkeit für das Ereignis
das „andere Kind“ mit Sicherheit ein Mädchen. Dies gilt natürlich auch dann, wenn wir, da wir die Wahl des Beobachters nicht kennen, mit dem „anderen Kind“ dasselbe meinen wie der Beobachter selbst. Das ist der entscheidende Punkt: die 25%-ige Eintrittswahrscheinlichkeit für das Ereignis ![]() (beide Kinde sind Mädchen) wird durch die willkürliche Bezugnahme auf ein „gewähltes“ und das „andere“ Kind nicht verändert. Unabhängig von der Entscheidung des gedachten Beobachters und unserer eigenen Wahl bleibt die Chance, im Endeffekt zwei Mädchen vorzufinden bei
(beide Kinde sind Mädchen) wird durch die willkürliche Bezugnahme auf ein „gewähltes“ und das „andere“ Kind nicht verändert. Unabhängig von der Entscheidung des gedachten Beobachters und unserer eigenen Wahl bleibt die Chance, im Endeffekt zwei Mädchen vorzufinden bei ![]() . Gleichgültig, welches Kind auch immer als „das Andere“ genommen wird.
. Gleichgültig, welches Kind auch immer als „das Andere“ genommen wird.
Letztlich ist der Beobachter für die Deutung des Ereignisraums absolut verzichtbar. Für die weitere Argumentation dürfen daher 4a und 4b wieder zusammengefasst werden. Aus diesem Grunde ist also „das andere Kind“ tatsächlich mit der Wahrscheinlichkeit ![]() zu
zu ![]() ) ein Mädchen.
) ein Mädchen.
Man versteht nun, wie es zu den unterschiedlichen Ergebnissen kommt: weiß man nur, „eines der Kinder ist ein Junge oder ein Mädchen“, so kann sich der Beobachter mit gleicher Wahrscheinlichkeit auf einen Jungen oder ein Mädchen beziehen. Das andere Kind ist daher mit der Wahrscheinlichkeit ![]() ein Mädchen. Sagt er aber „JA, eines der Kinder ist ein Mädchen“, dann macht die Frage nach dem anderen Kind nur dann Sinn, wenn dazu die willkürliche Bezugnahme des Beobachters implizit übernommen wird. Jener freilich bezieht sich zwingend auf ein Mädchen. Die Aufsplittung nach den obigen Zeilen 4a und 4b erweist sich dabei als nicht relevant, weil sowohl die Bezugnahme (Spalte 6) wie auch die Antwort auf die gestellte Frage (Spalte 7) in beiden Fällen gleich sind und folglich nicht weiter im Hinblick auf die Referenz des Beobachters differenziert werden muss. Deshalb ist insgesamt „das andere Kind“, wie gezeigt, mit der Chance
ein Mädchen. Sagt er aber „JA, eines der Kinder ist ein Mädchen“, dann macht die Frage nach dem anderen Kind nur dann Sinn, wenn dazu die willkürliche Bezugnahme des Beobachters implizit übernommen wird. Jener freilich bezieht sich zwingend auf ein Mädchen. Die Aufsplittung nach den obigen Zeilen 4a und 4b erweist sich dabei als nicht relevant, weil sowohl die Bezugnahme (Spalte 6) wie auch die Antwort auf die gestellte Frage (Spalte 7) in beiden Fällen gleich sind und folglich nicht weiter im Hinblick auf die Referenz des Beobachters differenziert werden muss. Deshalb ist insgesamt „das andere Kind“, wie gezeigt, mit der Chance ![]() ein Mädchen.
ein Mädchen.
Die folgende Tabelle gibt in Abhängigkeit von der Beantwortung der betreffende Frage (Ist es eines der Kinder ein Mädchen? / Ist es eines der Kinder ein Junge?) durch den Beobachter einen vollständigen Überblick für die resultierende Wahrscheinlichkeit. Um den Bogen zur Problemstellung (2) wieder zu schlagen, betrachten wie zusätzlich die Beantwortung der Frage „Ist eines der Kinder ein Junge oder Mädchen?“ (worauf die Antwort natürlich nur JA sein kann).
| Nr. | Antwort des Beobachters auf die Frage: Ist eines der Kinder ein Mädchen? | Mögliche Geschlechter-kombinationen | W. für das Eintreten des Ereignisses | W. dafür, dass das andere Kind ein Mädchen ist | W. dafür, dass das andere Kind ein Junge ist |
| 1 | Nein | ||||
| 2 | Ja | ||||
| Antwort des Beobachters auf die Frage: Ist eines der Kinder ein Junge? | Mögliche Geschlechter-kombinationen | W. für das Eintreten des Ereignisses | W. dafür, dass das andere Kind ein Mädchen ist | W. dafür, dass das andere Kind ein Junge ist | |
| 3 | Nein | ||||
| 4 | Ja | ||||
| Nr. | Antwort des Beobachters auf die Frage: Ist eines der Kinder ein Junge oder ein Mädchen? | Mögliche Geschlechter-kombinationen | W. für das Eintreten des Ereignisses | W. dafür, dass das andere Kind ein Mädchen ist | W. dafür, dass das andere Kind ein Junge ist |
| 5 | Ja |
Tabelle 1‑5
Die Einführung des unabhängigen Beobachters gestattete uns eine objektive Sicht auf die Verhältnisse und erleichterte daher die Argumentation. Denken wir uns ihn wieder weg, so ändert dies selbstredend nichts an den Resultaten. Die Tabelle gibt daher auch für das Originalproblem (1) die richtige Antwort ![]() (s. Zeile Nr. 2, Spalte 5). Wichtig ist dabei aber die Einsicht, dass diese Aussage nur dann gilt, wenn die Fragestellung (Ist es eines der Kinder ein Mädchen? / Ist es eines der Kinder ein Junge?) als immanenter Bestandteil des Rätsels verstanden wird.
(s. Zeile Nr. 2, Spalte 5). Wichtig ist dabei aber die Einsicht, dass diese Aussage nur dann gilt, wenn die Fragestellung (Ist es eines der Kinder ein Mädchen? / Ist es eines der Kinder ein Junge?) als immanenter Bestandteil des Rätsels verstanden wird.
In der Tat macht es einen wesentlichen Unterschied, ob man nun frägt:
- „Ist eines der Kinder ein Junge oder ein Mädchen?“ oder
- „Ist eines der Kinder ein Mädchen?“ oder
- „Ist eines der Kinder ein Junge?“.
Denn ist die Antwort im ersten Falle JA, so ist das andere Kind mit der Wahrscheinlichkeit ![]() ein Mädchen. Dagegen ist die Chance hierfür nur
ein Mädchen. Dagegen ist die Chance hierfür nur ![]() , wenn stattdessen Frage 2 mit JA beantwortet wird. Wird hingegen Frage 3 gestellt und mit JA beschieden, so ist das andere Kind mit der Wahrscheinlichkeit
, wenn stattdessen Frage 2 mit JA beantwortet wird. Wird hingegen Frage 3 gestellt und mit JA beschieden, so ist das andere Kind mit der Wahrscheinlichkeit ![]() ein Mädchen.
ein Mädchen.
Betrachtet man Zeile Nr. 2 und Zeile Nr. 5 von Tabelle 1‑5 im Vergleich, so sieht man beispielhaft, wie sich durch das Mehr an Information (die möglichen Ereignisse sind auf ![]() der prinzipiell möglichen Fälle eingegrenzt) die Wahrscheinlichkeitsaussage von
der prinzipiell möglichen Fälle eingegrenzt) die Wahrscheinlichkeitsaussage von ![]() auf
auf ![]() verändert. Der relevante Informationsgewinn manifestiert sich hier im unterschiedlichen Gehalt der betreffenden Fragen und in den resultierenden Antworten bzw. den damit verbundenen Ereignissen.
verändert. Der relevante Informationsgewinn manifestiert sich hier im unterschiedlichen Gehalt der betreffenden Fragen und in den resultierenden Antworten bzw. den damit verbundenen Ereignissen.
Es ist demnach nicht ins Belieben des Betrachters gestellt, sich unter den beiden Fragen (2 oder 3) eine auszusuchen. Tut man dies dennoch – sagen wir mit Gleichverteilung – so mitteln sich die Ergebnisse der Zeilen Nr. 1, 2, 3 und 4 der Tabelle untereinander aus. Im Endeffekt ergibt sich daher unter dieser Prämisse die fragliche Wahrscheinlichkeit zu ![]() . Unnötig darauf hinzuweisen, dass dies mit dem ursprünglichen Geschwisterparadoxon (1) nichts mehr zu tun hat.
. Unnötig darauf hinzuweisen, dass dies mit dem ursprünglichen Geschwisterparadoxon (1) nichts mehr zu tun hat.
Beleuchten wir das Problem noch kurz von einer anderen Seite:
- (5) Familie F habe zwei Kinder. Zu Person A sagen wir, eines der Kinder ist ein Mädchen. Unabhängig davon teilen wir Person B mit, eines der Kinder ist ein Junge. Anschließend fragen wir beide Personen unabhängig voneinander, mit welcher Wahrscheinlichkeit das jeweils zweite Kind ein Mädchen ist?
Aufgrund der Analyse zum Geschwisterparadoxon antwortet uns A, dass das zweite Kind mit der Wahrscheinlichkeit ![]() ein Mädchen sei. Unabhängig davon erklärt B, die Wahrscheinlichkeit ergebe sich zu
ein Mädchen sei. Unabhängig davon erklärt B, die Wahrscheinlichkeit ergebe sich zu ![]() , weil in zwei von drei Fällen die Konstellation
, weil in zwei von drei Fällen die Konstellation ![]() auftritt, nur in einem Falle indes beide Kinder Jungen sind und die Konstellation
auftritt, nur in einem Falle indes beide Kinder Jungen sind und die Konstellation ![]() überhaupt nicht vorliegen könne.
überhaupt nicht vorliegen könne.
Welche Antwort ist nun richtig? Nun, beide sind zutreffend, eine jede aber nur im Kontext der jeweils gegebenen Vorinformation. Was sehen wir daraus? Es ist maßgeblich für die resultierende Antwort, welche Auskunft über Familie F erteilt wird? Mit anderen Worten, wird diese Information verändert, so hat dies bei unveränderter Geschwisterkonstellation (in beiden Fällen geht es ja um dieselbe Familie F), i. A. direkten Einfluss auf die nachgefragte Wahrscheinlichkeit.
Wenden wir uns einer Rätselvariante zu, die angeblich klar machen soll, dass die fragliche Wahrscheinlichkeit nicht ![]() sondern
sondern ![]() sein muss:
sein muss:
- (6) Eine Familie mit zwei Kindern zieht in Nachbars Wohnung ein. Eines davon ist ein Mädchen. Mit welcher Wahrscheinlichkeit ist auch das zweite Kind ein Mädchen?
Die Argumentation geht dahin, man könne ja nicht wissen, welche Familie vor Stellung des Rätsels in Nachbars Wohnung eingezogen sei, deswegen müsse man davon ausgehen, dass in dieser Familie alle Kombinationen von Kindern ![]() ,
, ![]() und
und ![]() mit gleicher Wahrscheinlichkeit auftreten. Die Chance, zwei Jungen oder zwei Mädchen anzutreffen, sei daher jeweils 25%, die gemischten Paare treten mit 50%-iger Wahrscheinlichkeit auf. Soweit, so gut. Nun wird aber weiter argumentiert: wenn in jedem vierten Falle die Kombination
mit gleicher Wahrscheinlichkeit auftreten. Die Chance, zwei Jungen oder zwei Mädchen anzutreffen, sei daher jeweils 25%, die gemischten Paare treten mit 50%-iger Wahrscheinlichkeit auf. Soweit, so gut. Nun wird aber weiter argumentiert: wenn in jedem vierten Falle die Kombination ![]() vorkommt und die Chance für
vorkommt und die Chance für ![]() gleichfalls genau 1:4 ist, so könne daraus nur geschlossen werden, dass das zweite Kind mit gleicher Wahrscheinlichkeit von
gleichfalls genau 1:4 ist, so könne daraus nur geschlossen werden, dass das zweite Kind mit gleicher Wahrscheinlichkeit von ![]() eben Junge oder Mädchen ist. Oder, ähnlich verquer: wenn in jedem vierten Falle die Kombination
eben Junge oder Mädchen ist. Oder, ähnlich verquer: wenn in jedem vierten Falle die Kombination ![]() vorkommt und die Chance für
vorkommt und die Chance für ![]() gleichfalls genau
gleichfalls genau ![]() ist, so folgt aufgrund der Zusatzinformation („eines davon ist ein Mädchen“) die Wahrscheinlichkeit für das Ereignis „auch das zweite Kind ist ein Mädchen“ zu
ist, so folgt aufgrund der Zusatzinformation („eines davon ist ein Mädchen“) die Wahrscheinlichkeit für das Ereignis „auch das zweite Kind ist ein Mädchen“ zu ![]() ,, weil MM genau halb so häufig auftritt wie
,, weil MM genau halb so häufig auftritt wie ![]() .
.
Hier wird sehr plastisch persifliert, worauf es wirklich ankommt. Natürlich nicht darauf, dass eine Familie in Nachbars Wohnung einzieht. Wichtig ist allein der Umstand, dass es sich dabei um eine Familie mit zwei Kindern handelt, und, dass unter allen denkbaren Familien mit zwei Kindern nur solche Familien zu betrachten sind (- per definitionem -), in denen ein Mädchen vorkommt, wobei diese Information schon bekannt ist, bevor die eigentliche Frage nach der Wahrscheinlichkeit gestellt wird. Im Kontext der Problemstellung gibt es sozusagen keine Familien ohne Mädchen. Derweil geht dieses Verständnis obiger Schlussweise ab. Als Beleg für einen Wert von ![]() für die Wahrscheinlichkeit, dass „auch das zweite Kind ein Mädchen ist“ kann diese Variante und die vorgetragene Argumentation infolgedessen nicht dienen, weil die Voraussetzungen unter denen die Aufgabe gestellt wird außer acht gelassen werden.
für die Wahrscheinlichkeit, dass „auch das zweite Kind ein Mädchen ist“ kann diese Variante und die vorgetragene Argumentation infolgedessen nicht dienen, weil die Voraussetzungen unter denen die Aufgabe gestellt wird außer acht gelassen werden.
Der Einwurf, das Originalrätsel entspräche nicht dem geschilderten Gedankenexperiment mit der Begründung, das Rätsel könne nur in ![]() aller Fälle überhaupt so gestellt werden, geht gleichfalls an der Sache vorbei. Ist es nicht stets so, dass Fragen genau wie Antworten nur in einem bestimmten Kontext zu verstehen sind? Was „alle denkbaren Fälle“ sind, wird durch die Rahmenbedingungen der Problemstellung endgültig definiert, durch nichts sonst. Andernfalls könnte man ja immer sagen, es seien nicht alle denkbaren Fälle abgedeckt. Das Rätsel kann z. B. gleichfalls nicht in den Fällen gestellt werden, in denen eine Familie nur ein Kind oder gar drei Kinder hat. Diese Interpretation führt daher selbstredend in die Irre.
aller Fälle überhaupt so gestellt werden, geht gleichfalls an der Sache vorbei. Ist es nicht stets so, dass Fragen genau wie Antworten nur in einem bestimmten Kontext zu verstehen sind? Was „alle denkbaren Fälle“ sind, wird durch die Rahmenbedingungen der Problemstellung endgültig definiert, durch nichts sonst. Andernfalls könnte man ja immer sagen, es seien nicht alle denkbaren Fälle abgedeckt. Das Rätsel kann z. B. gleichfalls nicht in den Fällen gestellt werden, in denen eine Familie nur ein Kind oder gar drei Kinder hat. Diese Interpretation führt daher selbstredend in die Irre.
Wie könnte das nun im konkreten Experiment aussehen?
Betrachten wir ![]() Kinder,
Kinder, ![]() Jungen und
Jungen und ![]() Mädchen. Wir bilden die
Mädchen. Wir bilden die ![]() gleichverteilten Paare von Jungen und Mädchen (
gleichverteilten Paare von Jungen und Mädchen (![]() mal
mal ![]() ,
, ![]() mal
mal ![]() ,
, ![]() mal
mal ![]() ,
, ![]() mal
mal ![]() ). Bringen wir nun zunächst die entsprechenden
). Bringen wir nun zunächst die entsprechenden ![]() Familien mit jeweils einem der
Familien mit jeweils einem der ![]() Kinderpärchen in
Kinderpärchen in ![]() Wohnblöcken mit
Wohnblöcken mit ![]() jeweils
jeweils ![]() „familiengerechten“ Wohnungen unter. Die Familien mit den Jungenpärchen
„familiengerechten“ Wohnungen unter. Die Familien mit den Jungenpärchen ![]() in Wohnblock
in Wohnblock ![]() , die mit den gemischten Pärchen
, die mit den gemischten Pärchen ![]() in Wohnblock
in Wohnblock ![]() , die
, die ![]() -Familien in Block 3 und schließlich die Familien mit Mädchenpärchen
-Familien in Block 3 und schließlich die Familien mit Mädchenpärchen ![]() in Block
in Block ![]() .
.
Nun wird also Nachbars Wohnung frei. Frage: Wer kann bzw. darf dort einziehen? Im Prinzip eine beliebige andere Familie, z.B. eine mit drei Kindern, eine kinderlose, oder eben auch eine mit zwei Kindern aus einem der Wohnblöcke ![]() . Im Kontext des Rätsels geht es nun aber nicht darum, allgemein darüber zu spekulieren, wer einziehen könnte. Dies ist zwar nicht ohne Spielraum festgelegt, aber doch stark eingegrenzt: in der einziehenden Familie muss es genau zwei Kindern geben, von denen (mindestens) eines ein Mädchen ist. Damit scheiden die Familien aus Wohnblock
. Im Kontext des Rätsels geht es nun aber nicht darum, allgemein darüber zu spekulieren, wer einziehen könnte. Dies ist zwar nicht ohne Spielraum festgelegt, aber doch stark eingegrenzt: in der einziehenden Familie muss es genau zwei Kindern geben, von denen (mindestens) eines ein Mädchen ist. Damit scheiden die Familien aus Wohnblock ![]() als mögliche Kandidaten ebenso aus, wie irgendwelche andere Familien, die nicht genau zwei Kinder, darunter mindestens ein Mädchen, haben. Sie haben sozusagen nicht die Berechtigung, in Nachbars Wohnung einzuziehen. Es verbleiben demnach nur die Familien aus den Blöcken
als mögliche Kandidaten ebenso aus, wie irgendwelche andere Familien, die nicht genau zwei Kinder, darunter mindestens ein Mädchen, haben. Sie haben sozusagen nicht die Berechtigung, in Nachbars Wohnung einzuziehen. Es verbleiben demnach nur die Familien aus den Blöcken ![]() als mögliche Kandidaten.
als mögliche Kandidaten.
Das den Rahmenbedingungen des Rätsels vollkommen entsprechende „experimentelle“ Umfeld stellt sich nun so dar: 1. Nachbars Wohnung ist frei. 2. Nach den Bedingungen des Rätsels wählen wir zufällig und blind eine beliebige Familie ![]() aus einem der Wohnblöcke
aus einem der Wohnblöcke ![]() . 3. Familie
. 3. Familie ![]() zieht in Nachbars Wohnung ein. 4. Nun wird die entscheidende Frage gestellt: Mit welcher Wahrscheinlichkeit sind dann beide Kinder Mädchen? Aus dem Experiment heraus ergibt sich völlig zwanglos die Antwort
zieht in Nachbars Wohnung ein. 4. Nun wird die entscheidende Frage gestellt: Mit welcher Wahrscheinlichkeit sind dann beide Kinder Mädchen? Aus dem Experiment heraus ergibt sich völlig zwanglos die Antwort ![]() , weil von den
, weil von den ![]() zur Auswahl stehenden Familien nur die
zur Auswahl stehenden Familien nur die ![]() Familien aus Block
Familien aus Block ![]() tatsächlich zwei Mädchen haben.
tatsächlich zwei Mädchen haben.
1.3 Abwandlungen zum Geschwisterproblem
Nun zu der verwandten Rätselvariante:
- (7) Eine Familie habe zwei Kinder. Das Ältere ist ein Mädchen. Mit welcher Wahrscheinlichkeit ist auch das zweite Kind ein Mädchen?
Im Unterschied zur ursprünglichen Form, wird hier also nicht gesagt, „eines der Kinder ist ein Mädchen“, sondern „das Ältere ist ein Mädchen“. Nur, was macht dies für einen Unterschied in Bezug auf die Fragestellung? Eigentlich doch gar keinen, will man meinen.
Betrachten wir zur Erhellung die Grundgesamtheit. Die einzelnen Ereignisse können beschrieben werden durch Wertepaare mit der zusätzlichen Information, welcher der beiden Einträge „das ältere Kind“ ist, also durch Tripel (Kind 1, Kind 2, Nr. „des älteren Kindes“). Die Grundgesamtheit, nennen wir sie ![]() , ist in folgender Tabelle dargestellt.
, ist in folgender Tabelle dargestellt.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
Tabelle 1‑6
Den Voraussetzungen des Rätsels („das ältere Kind ist ein Mädchen“) entsprechen nur die Zeilen 4, 5, 7 und 8. Das ist die interessierende Grundgesamtheit ![]() : bei den anderen möglichen Realisierungen ist das ältere Kind ein Junge.
: bei den anderen möglichen Realisierungen ist das ältere Kind ein Junge.
Nachdem nun aber alle Ereignisse gleichwahrscheinlich und nur in den Fällen der Zeilen 7 und 8 beide Kinder Mädchen sind, ist die fragliche Wahrscheinlichkeit („auch das zweite Kind ist ein Mädchen“) ![]() .
.
Intuitiv mag einen bei dieser Lösung ein ungutes Gefühl beschleichen. Teilweise wird hier ein mathematischer Formalismus bemüht, der nicht unmittelbar eingängig ist. Wird eventuell durch die Paarbildung und die doppelte Berücksichtigung der Paare ![]() und
und ![]() das Ergebnis in die gewünschte Richtung gedrängt? Versuchen wir einen alternativen Zugang ganz ohne Formalismus.
das Ergebnis in die gewünschte Richtung gedrängt? Versuchen wir einen alternativen Zugang ganz ohne Formalismus.
Wir beschreiben die möglichen Ereignisse durch ![]() je nachdem, ob nur Jungen, nur Mädchen oder beide Geschlechter vorkommen. Dazu notieren wir, welches Geschlecht (
je nachdem, ob nur Jungen, nur Mädchen oder beide Geschlechter vorkommen. Dazu notieren wir, welches Geschlecht (![]() bzw.
bzw. ![]() ) das ältere Kind hat sowie die Wahrscheinlichkeit für das Eintreten des entsprechenden Ereignisses. Die folgende Tabelle gibt den Überblick hierzu:
) das ältere Kind hat sowie die Wahrscheinlichkeit für das Eintreten des entsprechenden Ereignisses. Die folgende Tabelle gibt den Überblick hierzu:
| Nr. | Geschlechter | Geschlecht des älteren Kindes | W. für das Eintreten des Ereignisses |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
Tabelle 1‑7
Nur in den Fällen der Zeilen 3 und 4 ist eines der Kinder ein Mädchen und zugleich das ältere Kind ein Mädchen, und nur in Zeile 4 sind beide Kinder Mädchen. Wie oben ergibt sich daher auch jetzt die Wahrscheinlichkeit ![]() für das Eintreten des Ereignisses „auch das zweite Kind ist ein Mädchen“.
für das Eintreten des Ereignisses „auch das zweite Kind ist ein Mädchen“.
Trotz dieser Bestätigung mag man sich fragen: Wo eigentlich liegt denn der Unterschied zwischen den beiden Aufgabenstellungen? Formal ist zwar eines der beiden Kinder näher bestimmt („das ältere Kind ist ein Mädchen“), doch leuchtet nicht unmittelbar ein, wie diese Information letztlich das Ergebnis beeinflussen kann. Absolut gesehen sind nach wie vor nur in jedem vierten Falle beide Kinder Mädchen?
An dieser Stelle ist es hilfreich, sich die Laplace’sche Definiton von Wahrscheinlichkeit in Erinnerung zu rufen. Sie lautet ganz lapidar:
(5) ![]()
Bei der Betrachtung von ![]() Familien mit zwei Kindern werden im Mittel
Familien mit zwei Kindern werden im Mittel ![]() Familien zwei Mädchen haben, das ist die Anzahl der günstigen Fälle („auch das zweite Kind ist ein Mädchen“ bzw. “beide Kinder sind Mädchen“). Dieser Befund ist unabhängig von den genannten Voraussetzungen in den beiden Rätselformen. Unterschiedlich ist indessen die Anzahl der möglichen Fälle. In der ursprünglichen Problemstellung (1) sind die „möglichen Fälle“ eingegrenzt auf die Familien mit mindestens einem Mädchen. Dies sind
Familien zwei Mädchen haben, das ist die Anzahl der günstigen Fälle („auch das zweite Kind ist ein Mädchen“ bzw. “beide Kinder sind Mädchen“). Dieser Befund ist unabhängig von den genannten Voraussetzungen in den beiden Rätselformen. Unterschiedlich ist indessen die Anzahl der möglichen Fälle. In der ursprünglichen Problemstellung (1) sind die „möglichen Fälle“ eingegrenzt auf die Familien mit mindestens einem Mädchen. Dies sind ![]() Familien (=
Familien (= ![]() – die
– die ![]() Familien mit Jungenpärchen). Daher ist hier die fragliche Wahrscheinlichkeit
Familien mit Jungenpärchen). Daher ist hier die fragliche Wahrscheinlichkeit ![]() . Im anderen Falle (7) dürfen dagegen nur die
. Im anderen Falle (7) dürfen dagegen nur die ![]() Familien betrachtet werden, in denen das ältere Kind ein Mädchen ist. Deswegen kommt man in dieser Situation auf die Wahrscheinlichkeit
Familien betrachtet werden, in denen das ältere Kind ein Mädchen ist. Deswegen kommt man in dieser Situation auf die Wahrscheinlichkeit ![]() , obwohl doch in beiden Problemstellungen die Menge der günstigen Fälle genau gleich ist. Genau in dieser Gegebenheit liegt die scheinbare Paradoxie der Aufgabenstellung zu einem guten Teil begründet: nicht das fragliche Ereignis an sich wird durch die Voraussetzungen der Problemstellung näher beschrieben, sondern dessen Bezugsgröße, die relevante Grundgesamtheit.
, obwohl doch in beiden Problemstellungen die Menge der günstigen Fälle genau gleich ist. Genau in dieser Gegebenheit liegt die scheinbare Paradoxie der Aufgabenstellung zu einem guten Teil begründet: nicht das fragliche Ereignis an sich wird durch die Voraussetzungen der Problemstellung näher beschrieben, sondern dessen Bezugsgröße, die relevante Grundgesamtheit.
In diesem Zusammenhang muss man auch beachten, dass wir in der alternativen Aufgabenform (7) eigentlich zwei Informationen mitgeteilt bekommen:
- Eines der Kinder ist ein Mädchen.
- Das ältere Kind ist ein Mädchen.
Eine Wahrscheinlichkeitsaussage ist eine quantifizierte Vermutung zum Ausgang eines Experiments. Jede relevante Information zum Experiment (zum Ereignis selbst oder zur Grundgesamtheit) ist daher prinzipiell geeignet, den Grad an Genauigkeit für die Vorhersage zum Ausgang des Experiments zu erhöhen. In der Regel wird sich daher die Wahrscheinlichkeitsaussage mit jeder zusätzlichen relevanten Information verändern.
Im vorliegenden Falle ist die Information „Das ältere Kind ist ein Mädchen“ aus dem ganz einfachen Grunde relevant, weil dadurch all die Familien ausscheiden, in denen das ältere Kind ein Junge ist, und das trifft immerhin auf 50% aller zufällig gewählten Zwei-Kind-Familien zu.
Schauen wir uns zur Anwendung und Vertiefung noch einige weitere Problemvarianten an:
- (8) Eine Familie habe zwei Kinder. Eines der Kinder trägt weiße Schuhe und ist ein Mädchen, das andere Kind trägt schwarze Schuhe. Eines der Kinder trägt eine rote Mütze und ist ein Mädchen, das andere Kind trägt eine blaue Mütze. Das ältere Kind ist ein Mädchen. Mit welcher Wahrscheinlichkeit ist auch das zweite Kind ein Mädchen?
Stillschweigend dürfen wir hier davon ausgehen, dass die Zuordnung der Schuh- und Mützenfarben zu den beiden Kindern rein zufällig und gleichverteilt vorgenommen wurde.
Offensichtlich haben wir es hier mit einer durchaus abstrus zu nennenden Variante des Geschwisterparadoxons zu tun. Auf Anhieb möchte man sich fast verweigern, die Fragestellung ernst zu nehmen. Bei genauerer Betrachtung sieht man jedoch, dass die gleichen Prinzipien wie oben vorliegen, allerdings mit größeren Grundgesamtheiten.
Die folgende Tabelle gibt den Überblick zu den möglichen Ereignissen.
| Nr. | Geschlechter | Geschlecht des älteren Kindes | Kind mit weißen Schuhen | Kind mit roter Mütze | W. für das Eintreten des Ereignisses |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 |
Tabelle 1‑8
Man sieht sofort, dass nur in den Fällen der Zeilen ![]() und
und ![]() das ältere Kind ein Mädchen mit weißen Schuhen und roter Mütze ist. Nur in einem von
das ältere Kind ein Mädchen mit weißen Schuhen und roter Mütze ist. Nur in einem von ![]() Fällen tritt das Ereignis nach Zeile
Fällen tritt das Ereignis nach Zeile ![]() ein, in
ein, in ![]() von
von ![]() hingegen das Ereignis nach Zeile
hingegen das Ereignis nach Zeile ![]() (beide Kinder sind Mädchen). Diese
(beide Kinder sind Mädchen). Diese ![]() Fälle zusammen sind die „möglichen“ Ereignisse. Die Wahrscheinlichkeit dafür, dass auch das zweite Kind ein Mädchen ist, erhalten wir daher einfach zu
Fälle zusammen sind die „möglichen“ Ereignisse. Die Wahrscheinlichkeit dafür, dass auch das zweite Kind ein Mädchen ist, erhalten wir daher einfach zu ![]() =80%.
=80%.
In der weiter oben vorgetragenen Argumentation mit bedingten Wahrscheinlichkeiten ergibt sich, ausgehend von den betreffenden Ereignissen:
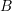 = „Beide Kinder sind Mädchen“
= „Beide Kinder sind Mädchen“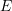 = „Das ältere Kind, das Kind mit den weißen Schuhen sowie das Kind mit der roten Mütze sind jeweils Mädchen“ …
= „Das ältere Kind, das Kind mit den weißen Schuhen sowie das Kind mit der roten Mütze sind jeweils Mädchen“ …
und dem bedingten Ereignis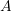 = „… auch das zweite Kind ist ein Mädchen …“ =
= „… auch das zweite Kind ist ein Mädchen …“ = 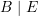
analog:
(6) ![]()
Das Ereignis ![]() entspricht den Zeilen 9 und 10 von Tabelle 1‑8, Ereignis
entspricht den Zeilen 9 und 10 von Tabelle 1‑8, Ereignis ![]() nur Zeile 10. Demzufolge ist
nur Zeile 10. Demzufolge ist
(7) ![]()
1.4 Verallgemeinerungen zur Originalvariante
Eine verallgemeinerte Problemvariante zur ursprünglichen Form ist die folgende:
- (9) Eine Familie habe
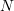 Kinder.
Kinder.  der Kinder seien Mädchen. Mit welcher Wahrscheinlichkeit ist auch das verbleibende Kind ein Mädchen?
der Kinder seien Mädchen. Mit welcher Wahrscheinlichkeit ist auch das verbleibende Kind ein Mädchen?
Wir betrachten die folgenden Ereignisse:
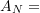 „alle
„alle 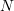 Kinder sind Mädchen“
Kinder sind Mädchen“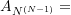 „
„ der Kinder sind Mädchen“
der Kinder sind Mädchen“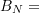 „…auch das verbleibende Kind (das
„…auch das verbleibende Kind (das 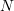 -te) ist ein Mädchen…“
-te) ist ein Mädchen…“
Hier ist ![]() das bedingte Ereignis
das bedingte Ereignis ![]() . Es gilt
. Es gilt ![]() . Das Ereignis
. Das Ereignis ![]() tritt genau dann ein, wenn alle Kinder Mädchen sind oder genau eines der Kinder ein Junge ist, daher ist
tritt genau dann ein, wenn alle Kinder Mädchen sind oder genau eines der Kinder ein Junge ist, daher ist
(8) ![]()
und wir bekommen:
(9) ![]()
In einer Familie von neun Kindern, darunter ![]() Mädchen, ist das neunte Kind nur mit 10%.iger Chance ein Mädchen.
Mädchen, ist das neunte Kind nur mit 10%.iger Chance ein Mädchen.
Für ![]() erhalten wir wieder das ursprüngliche Geschwisterparadoxon (1) mit dem Ergebnis
erhalten wir wieder das ursprüngliche Geschwisterparadoxon (1) mit dem Ergebnis ![]() .
.
Nun noch zu einer letzten Spielart des Rätsels:
- (10) Eine Familie habe
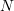 Kinder. Eines der Kinder sei ein Mädchen. Mit welcher Wahrscheinlichkeit gibt es noch ein weiteres Mädchen?
Kinder. Eines der Kinder sei ein Mädchen. Mit welcher Wahrscheinlichkeit gibt es noch ein weiteres Mädchen?
Wir betrachten die folgenden Ereignisse:
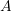 = „alle Kinder sind Jungen“
= „alle Kinder sind Jungen“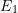 = „genau eines der Kinder ist ein Mädchen“
= „genau eines der Kinder ist ein Mädchen“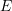 = „eines der Kinder ist ein Mädchen“
= „eines der Kinder ist ein Mädchen“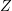 ’= „zwei der Kinder sind Mädchen“
’= „zwei der Kinder sind Mädchen“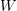 = „…es gibt ein weiteres Mädchen…“
= „…es gibt ein weiteres Mädchen…“
Hier ist ![]() das bedingte Ereignis
das bedingte Ereignis ![]() . Es gilt ferner
. Es gilt ferner ![]() und
und ![]() sowie
sowie
(10) ![]()
Daraus folgt:
(11) ![]()
In einer Familie von zehn Kindern, darunter sicher ein Mädchen, gibt es daher mit etwa 99%-iger Wahrscheinlichkeit noch ein weiteres Mädchen.
Für ![]() erhalten wir auch hier wieder das ursprüngliche Geschwisterparadoxon (1) mit dem Ergebnis
erhalten wir auch hier wieder das ursprüngliche Geschwisterparadoxon (1) mit dem Ergebnis ![]() .
.



Bei Aufgabe (8) habe ich 6/7 erhalten.
xy steht für „das Kind hat Schuhe der Farbe x und eine Mütze der Farbe y.
(u,v) bedeutet „u ist das erste Kind, v das zweite.“
Dann gibt es die vier Fälle, die alle die W’keit 1/4 haben.
1. (wr,sb)
2. (wb,sr)
3. (sr,wb)
4. (sb,wr)
Nun steht (a,b) für „Erstes Kind hat Geschlecht a, zweites b.“
Wir erhalten
1. (m, ?)
2. (m,m)
3. (m, m)
4. (?, m)
Wir erhalten P(K1 = m) = 1/4 + 1/4 + 1/4 + 1/4×1/8 = 7/8
und P(K1=m & K2=m) = 1/4×1/8 + 1/4 + 1/4 + 1/4×1/8 = 3/4
Damit P(K2=m)|P(K1=m)= (3/4)/(7/8)=6/7
Wo mache ich einen Denkfehler?
Sorry, dass die Antwort so lange auf sich warten ließ, ich war umständehalber mehrere Monate nicht auf der Seite.
Wie dargelegt, muss man stets die komplette Grundgesamtheit betrachten. Sie nehmen die Eigenschaften Schuhe/Mütze und J/M völlig getrennt voneinander in den Blick. In der Aufgabenstellung wird aber explizit eine Verbindung zwischen Schuhen, Mützen und dem Geschlecht hergestellt. Die Anzahl der möglichen und der günstigen Ereignisse können nur durch die gemeinsame Betrachtung korrekt bestimmt werden.
Die beiden Summen sind fehlerhaft. Bei Ihrer ersten Summe ergibt sich 25/32 statt 7/8, bei der zweiten 18/32 statt 3/4. Im Ergebnis erhielten Sie daher in Ihrer Rechnung das Resultat 18/25 statt 6/7.