1 Einführung
Eine Zahl, die bei Umkehrung der Ziffernfolge unverändert bleibt, nennt man «Palindrom». Eine andere Bezeichnung dafür ist einfach «symmetrische Zahl».
Beispiele: ![]() usw.
usw.
Ob eine bestimmte Zahl Palindrom ist oder nicht, hängt natürlich vom verwendeten Ziffernsystem ab. In der folgenden Tabelle sind einige Zahlen in verschiedenen Ziffernsystemen aufgelistet. Die Palindrome sind farbig hervorgehoben.
| Basis 10 (Dezimal) | Basis 2 (Binär) | Basis 3 | Basis 5 | Basis 8 (Oktal) | Basis 16 (Hex) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 | 2 | 2 |
| 3 | 11 | 10 | 3 | 3 | 3 |
| 4 | 100 | 11 | 4 | 4 | 4 |
| 5 | 101 | 12 | 10 | 5 | 5 |
| 6 | 110 | 20 | 11 | 6 | 6 |
| 7 | 111 | 21 | 12 | 7 | 7 |
| 8 | 1000 | 22 | 13 | 10 | 8 |
| 9 | 1001 | 100 | 14 | 11 | 9 |
| 10 | 1010 | 101 | 20 | 12 | A |
| Basis 10 (Dezimal) | Basis 2 (Binär) | Basis 3 | Basis 5 | Basis 8 (Oktal) | Basis 16 (Hex) |
| 11 | 1011 | 102 | 21 | 13 | B |
| 12 | 1100 | 110 | 22 | 14 | C |
| 13 | 1101 | 111 | 23 | 15 | D |
| 14 | 1110 | 112 | 24 | 16 | E |
| 15 | 1111 | 120 | 30 | 17 | F |
| 16 | 10000 | 121 | 31 | 20 | 10 |
| 17 | 10001 | 122 | 32 | 21 | 11 |
| 18 | 10010 | 200 | 33 | 22 | 12 |
| 19 | 10011 | 201 | 34 | 23 | 13 |
| 20 | 10100 | 202 | 40 | 24 | 14 |
| Basis 10 (Dezimal) | Basis 2 (Binär) | Basis 3 | Basis 5 | Basis 8 (Oktal) | Basis 16 (Hex) |
| 21 | 10101 | 210 | 41 | 25 | 15 |
| 22 | 10110 | 211 | 42 | 26 | 16 |
| 23 | 10111 | 212 | 43 | 27 | 17 |
| 24 | 11000 | 220 | 44 | 30 | 18 |
| 25 | 11001 | 221 | 100 | 31 | 19 |
| 26 | 11010 | 222 | 101 | 32 | 1A |
| 27 | 11011 | 1000 | 102 | 33 | 1B |
| 28 | 11100 | 1001 | 103 | 34 | 1C |
| 29 | 11101 | 1002 | 104 | 35 | 1D |
| 30 | 11110 | 1010 | 110 | 36 | 1E |
| Basis 10 (Dezimal) | Basis 2 (Binär) | Basis 3 | Basis 5 | Basis 8 (Oktal) | Basis 16 (Hex) |
| 31 | 11111 | 1011 | 111 | 37 | 1F |
| 32 | 100000 | 1012 | 112 | 40 | 20 |
| 33 | 100001 | 1020 | 113 | 41 | 21 |
| 34 | 100010 | 1021 | 114 | 42 | 22 |
| 55 | 110111 | 2001 | 210 | 67 | 37 |
| 99 | 1100011 | 10200 | 344 | 143 | 63 |
| 100 | 1100100 | 10201 | 400 | 144 | 64 |
| 101 | 1100101 | 10202 | 401 | 145 | 65 |
| 200 | 11001000 | 21102 | 1300 | 310 | C8 |
| 499 | 111110011 | 200111 | 3444 | 763 | 1F3 |
| Basis 10 (Dezimal) | Basis 2 (Binär) | Basis 3 | Basis 5 | Basis 8 (Oktal) | Basis 16 (Hex) |
| 500 | 111110100 | 200112 | 4000 | 764 | 1F4 |
| 501 | 111110101 | 200120 | 4001 | 765 | 1F5 |
| 502 | 111110110 | 200121 | 4002 | 766 | 1F6 |
| 503 | 111110111 | 200122 | 4003 | 767 | 1F7 |
| 504 | 111111000 | 200200 | 4004 | 770 | 1F8 |
| 511 | 111111111 | 200221 | 4021 | 777 | 1FF |
| 512 | 1000000000 | 200222 | 4022 | 1000 | 200 |
| 513 | 1000000001 | 201000 | 4023 | 1001 | 201 |
| 514 | 1000000010 | 201001 | 4024 | 1002 | 202 |
| 524 | 1000001100 | 201102 | 4044 | 1014 | 20C |
Wenden wir uns zunächst den dezimalen Palindromen zu.
2 Dezimale Palindrome
Die ersten dezimalen Palindrome sind:
(1) 
Die Palindrome werden fortlaufend nummeriert, beginnend mit dem Index 1. Das erste solche Palindrome ist also die Zahl ![]() , das zweite die
, das zweite die ![]() , usw. Formal bezeichnen wir das
, usw. Formal bezeichnen wir das ![]() -te dezimale Palindrom mit
-te dezimale Palindrom mit ![]() . Es gilt daher z.B.
. Es gilt daher z.B. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Wenn man die Palindrome solchermaßen notiert, erkennt man eine erste Gesetzmäßigkeit.
Palindrome mit der Nummer ![]() lauten daher
lauten daher ![]() . Für
. Für ![]() gilt dagegen
gilt dagegen ![]() . Die weitergehende Analyse zeigt
. Die weitergehende Analyse zeigt
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array} {lll} P_{10}(10^q + 10^{q-1}) &= 10^{2q-1} + 1, &\text{für}\; q > 0 \\[8pt]P_{10}(10^q + 10^{q-1} - 1) &= 10^{2q-1} - 1, &\text{für}\; q > 0 \\[8pt] P_{10}((d+1) \cdot 10^q) &= d \cdot 10^{2q} +d, &\text{für}\; 0 < d \le 9, \, q \ge 0 \\[8pt] P_{10}((d+10) \cdot 10^{q-1}) &= d \cdot 10^{2q-1} + d, &\text{für}\; 0 < d \le 9, \, q > 0 \end{array} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-9687636807e9e84920edaab537f02979_l3.png)
Im Folgenden geht es um die Bestimmung von dezimalen Palindromen, wir wollen also eine formelmäßige Beziehung für ![]() . Damit wird die Frage beantwortet: Wie lautet das
. Damit wird die Frage beantwortet: Wie lautet das ![]() -te dezimale Palindrom?
-te dezimale Palindrom?
Wir werden dazu drei Lösungen präsentieren: die rekursive Berechnung, die direkte formelmäßige Berechnung sowie eine anschauliche Schnellbestimmung völlig ohne Hilfsmittel.
Nach der vorstehenden Tabelle gibt es einen direkten Zusammenhang zwischen bestimmten Wertebereichen von ![]() und der Stellenanzahl des zugeordneten dezimalen Palindroms. Diese Stellenanzahl ist von Bedeutung, weil sie den Charakter der Symmetrieeigenschaft des Palindroms unmittelbar beeinflusst. Bei einer ungeraden Anzahl von Ziffern liegt die Symmetrieachse genau auf der mittleren Ziffer, bei einer geraden Anzahl von Stellen dagegen zwischen den beiden mittleren Ziffern.
und der Stellenanzahl des zugeordneten dezimalen Palindroms. Diese Stellenanzahl ist von Bedeutung, weil sie den Charakter der Symmetrieeigenschaft des Palindroms unmittelbar beeinflusst. Bei einer ungeraden Anzahl von Ziffern liegt die Symmetrieachse genau auf der mittleren Ziffer, bei einer geraden Anzahl von Stellen dagegen zwischen den beiden mittleren Ziffern.
Die Anzahl der Ziffern des ![]() -ten Palindrom lässt sich aus der Anzahl der Stellen von
-ten Palindrom lässt sich aus der Anzahl der Stellen von ![]() und dem betreffenden Wertebereich bestimmen. Die Stellenanzahl des resultierenden Palindroms ist das Doppelte der Ziffernanzahl von
und dem betreffenden Wertebereich bestimmen. Die Stellenanzahl des resultierenden Palindroms ist das Doppelte der Ziffernanzahl von ![]() minus
minus ![]() , minus
, minus ![]() oder minus
oder minus ![]() , je nachdem, in welchem Wertebereich
, je nachdem, in welchem Wertebereich ![]() liegt.
liegt.
Die nachfolgend für ![]() definierten Hilfsfunktionen
definierten Hilfsfunktionen ![]() und
und ![]() erlauben direkt die Bestimmung der gesuchten Stellenanzahl
erlauben direkt die Bestimmung der gesuchten Stellenanzahl ![]() . Mit
. Mit
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \lambda(n) &:= \left\lfloor \log_{10}\left(\max\left(1,\frac{10}{11}\cdot n \right) \right) \right\rfloor \\[8pt] \overline{\lambda}(n) &:= \left\lfloor \log_{10}\left(\max\left(1,\frac{1}{2} \cdot n\right) \right) \right\rfloor \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-5988ec702bbb2065bd2899ff125e16a6_l3.png)
ergibt sich
(4) ![Rendered by QuickLaTeX.com \begin{equation*} L\left(P_{10}(n)\right) = \begin{cases} 2 \cdot \lambda(n) +1, &\text{wenn} \; \lambda(n) = \overline{\lambda}(n) \\[8pt]2 \cdot \overline{\lambda}(n), &\text{sonst} \end{cases} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-41124f9b488e5147068bb9d899281d53_l3.png)
Da ![]() entweder gleich
entweder gleich ![]() oder um
oder um ![]() kleiner ist, wird die Stellenanzahl von
kleiner ist, wird die Stellenanzahl von ![]() im Falle der Ungleichheit
im Falle der Ungleichheit ![]() auch durch die Summe
auch durch die Summe ![]() bestimmt. Man kann daher für die Stellenanzahl von
bestimmt. Man kann daher für die Stellenanzahl von ![]() auch schreiben
auch schreiben
(5) ![]()
Nach dem Vorstehenden ist somit die Stellenanzahl ungerade im ersteren Falle, wenn also ![]() , andernfalls, wenn also
, andernfalls, wenn also ![]() , ist sie gerade.
, ist sie gerade.
2.1 Die rekursive Berechnung
Zunächst drängt sich ein rekursiver Ansatz auf. Nehmen wir als Beispiel das Palindrom ![]() . Es setzt sich offensichtlich zusammen aus den drei Palindromen
. Es setzt sich offensichtlich zusammen aus den drei Palindromen ![]() ,
, ![]() und
und ![]() und kann aus diesen mittels der Summe
und kann aus diesen mittels der Summe ![]() rekonstruiert werden. Noch einfacher ist die zweistufige Ableitung
rekonstruiert werden. Noch einfacher ist die zweistufige Ableitung ![]() mit
mit ![]() . Ein weiteres Beispiel:
. Ein weiteres Beispiel: ![]() . Der Rekursionsansatz könnte daher lauten:
. Der Rekursionsansatz könnte daher lauten:
(6) ![]()
Wobei die Größen ![]() und der Exponent
und der Exponent ![]() geeignet aus
geeignet aus ![]() zu wählen bzw. zu errechnen sind. Nach der vorstehenden Betrachtung über die einfach zu bestimmenden Palindrome für Vielfache von Zehnerpotenzen
zu wählen bzw. zu errechnen sind. Nach der vorstehenden Betrachtung über die einfach zu bestimmenden Palindrome für Vielfache von Zehnerpotenzen ![]() sowie
sowie ![]() , erscheint es sinnvoll, den Wert für
, erscheint es sinnvoll, den Wert für ![]() im entsprechenden Wertebereich zu wählen und die weiteren Parameter
im entsprechenden Wertebereich zu wählen und die weiteren Parameter ![]() und
und ![]() auf dieser Basis zu bestimmen. Wir formulieren daher die folgende Rekursionsbeziehung
auf dieser Basis zu bestimmen. Wir formulieren daher die folgende Rekursionsbeziehung
(7) ![]()
Damit können wir für ![]() das
das ![]() -te dezimale Palindrom rekursiv berechnen. Die Parameter
-te dezimale Palindrom rekursiv berechnen. Die Parameter ![]() und
und ![]() sind dabei folgendermaßen zu bestimmen:
sind dabei folgendermaßen zu bestimmen:
(8) ![Rendered by QuickLaTeX.com \begin{align*} q &= \lambda(n) + \overline{\lambda}(n) \\[8pt]d &= \displaystyle \left(\left\lfloor \frac{n}{10^{ \left\lfloor\frac{q}{2}\right\rfloor}} \right\rfloor -1 + q \bmod 2 \right) \bmod 10 \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-ecf28db406eb918ec8b1bf963f84a77e_l3.png)
Wegen ![]() kann man dabei auch direkt auf die
kann man dabei auch direkt auf die ![]() -Funktionen zurückgreifen. Die weiteren Parameter
-Funktionen zurückgreifen. Die weiteren Parameter ![]() und
und ![]() erhält man mittels des nachfolgend definierten Hilfsparameters
erhält man mittels des nachfolgend definierten Hilfsparameters ![]() .
.
(9) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} N &= \displaystyle \left(d+1+ 9\cdot \left(q \bmod 2 \right) \right) \cdot 10^{ \left\lfloor\frac{q}{2}\right\rfloor} \\[8pt] m &= \begin{cases} 1, &\text{wenn} \; n = N \\[4pt] n - N + 10^{\displaystyle \left\lfloor\log_{10}\left(n-N\right) \right\rfloor + q \bmod 2}, &\text{sonst} \end{cases} \\[8pt]p &= \lambda(n) - \lambda(m) \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-25be927817c9fc05bd7c9ce7d5070d43_l3.png)
Die Stellenanzahl ![]() des Palindroms ist
des Palindroms ist ![]() . Demnach hat das gesuchte Palindrom eine ungerade Anzahl von Stellen, wenn
. Demnach hat das gesuchte Palindrom eine ungerade Anzahl von Stellen, wenn ![]() gerade ist, und eine gerade Anzahl von Stellen, wenn
gerade ist, und eine gerade Anzahl von Stellen, wenn ![]() ungerade ist.
ungerade ist.
Rechenbeispiel für ![]() . Wie lautet das betreffende dezimale Palindrom? – Wir erhalten
. Wie lautet das betreffende dezimale Palindrom? – Wir erhalten
(10) 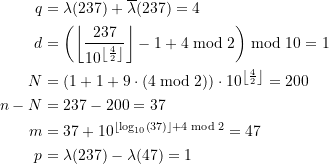
Eingesetzt in die Rekursionsformel ergibt sich
(11) ![]()
Das Palindrom mit der Nummer ![]() wurde somit auf das kleinere Palindrom mit
wurde somit auf das kleinere Palindrom mit ![]() zurückgeführt. Zur Finalisierung der Rekursion müssen wir auch dieses berechnen. Analog folgt:
zurückgeführt. Zur Finalisierung der Rekursion müssen wir auch dieses berechnen. Analog folgt:
(12) 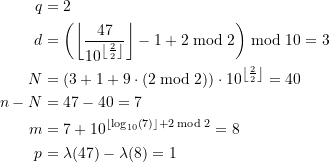
Damit bekommen wir nun, ![]() berücksichtigend,
berücksichtigend,
(13) 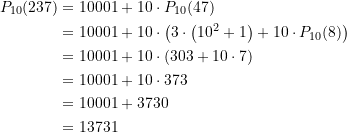
2.2 Die direkte Berechnung
Für ![]() kann man das
kann man das ![]() -te dezimale Palindrom auch auf direktem Wege berechnen. Dazu definieren wir
-te dezimale Palindrom auch auf direktem Wege berechnen. Dazu definieren wir ![]() und erinnern an
und erinnern an ![]() , sowie
, sowie ![]() . Wir unterscheiden zwei Fälle.
. Wir unterscheiden zwei Fälle.
Fall 1: ![]()
(14) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{10}(n) &=\sum \limits_{k=1}^{m-1} \left(\left\lfloor \frac{n}{10^{m-k}}\right\rfloor \bmod 10\right)\left(10^k + 10^{2m-k}\right) \; + \\[4pt]& \quad \, \left( \left\lfloor \frac{n}{10^m} \right\rfloor -1 \right) \left(1 + 10^{2m}\right) + \left(n \bmod 10 \right) \cdot 10^m \\[10pt]&= \sum \limits_{k=1}^{m-1} \left(\left\lfloor \frac{n}{10^{m-k}}\right\rfloor \bmod 10\right) \cdot 10^k \;+ \\[4pt] & \quad \, \left(n - 10^m\right) \cdot 10^m + \left\lfloor \frac{n}{10^m} \right\rfloor -1 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-f49f570c313a3042a33a51e8ddab705d_l3.png)
Fall 2: ![]()
(15) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{10}(n) &=\sum \limits_{k=0}^{m-1} \left(\left\lfloor \frac{n}{10^{m-k-1}}\right\rfloor \bmod 10\right)\left(10^{k} + 10^{2m-k-1}\right) \\[8pt]&= \sum \limits_{k=1}^{m-1} \left(\left\lfloor \frac{n}{10^{m-k}}\right\rfloor \bmod 10\right)\cdot 10^{k-1} \;+ \\[4pt] & \quad \, \left(n - 10^m\right) \cdot 10^m + \left( n \bmod 10\right) \cdot 10^{m-1} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-feb06de8039c16777e7892a73a00b1a2_l3.png)
Beispiel 1: ![]() . Wie man leicht errechnet. ergibt sich
. Wie man leicht errechnet. ergibt sich ![]() . Es gilt daher
. Es gilt daher ![]() . Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Für den Summenausdruck mit dem einzigen Term
. Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Für den Summenausdruck mit dem einzigen Term ![]() bekommen wir
bekommen wir ![]() . Die Summanden außerhalb sind
. Die Summanden außerhalb sind ![]() und
und ![]() . Das ergibt
. Das ergibt ![]() .
.
Beispiel 2: Wir haben ![]() . Wieder ist
. Wieder ist ![]() , somit trifft erneut der erstgenannte Fall zu. Der einzige Term des Summenausdrucks mit dem Index-Term
, somit trifft erneut der erstgenannte Fall zu. Der einzige Term des Summenausdrucks mit dem Index-Term ![]() ist
ist ![]() . Die Terme ausßerhalb der Summe sind
. Die Terme ausßerhalb der Summe sind ![]() und
und ![]() . Das ergibt
. Das ergibt ![]() .
.
Beispiel 3: Nun haben wir ![]() , das ist der zweite Fall mit
, das ist der zweite Fall mit ![]() . Der finale Summenausdruck mit den beiden Index-Termen für
. Der finale Summenausdruck mit den beiden Index-Termen für ![]() und
und ![]() ergibt
ergibt ![]() sowie
sowie
![]() mit der Summe
mit der Summe ![]() . Die Summanden außerhalb sind
. Die Summanden außerhalb sind ![]() und
und ![]() . Zusammen resultiert das in
. Zusammen resultiert das in ![]() .
.
2.3 Ein einfacher Algorithmus zur Bestimmung von dezimalen Palindromen
Aus dem Vorstehenden ergibt sich eine anschauliche und leicht ohne jegliche Hilfsmittel durchführbare Ableitung für die Berechnung des ![]() -ten Palindroms. Sei
-ten Palindroms. Sei ![]() die Ziffernfolge von
die Ziffernfolge von ![]() als
als ![]() -Tupel und
-Tupel und ![]() die Ziffernfolge des entsprechenden Palindroms
die Ziffernfolge des entsprechenden Palindroms ![]() als
als ![]() -Tupel. Man erhält die Ziffernfolge des
-Tupel. Man erhält die Ziffernfolge des ![]() -ten Palindroms
-ten Palindroms ![]() nach folgender einfacher Berechnungsvorschrift:
nach folgender einfacher Berechnungsvorschrift:
(16) ![Rendered by QuickLaTeX.com \begin{equation*} P_{10}(n) \Leftrightarrow \begin{cases} \large \left[ \, d_1-1\; d_2\; d_3 \cdots d_k \cdots d_3\; d_2\; d_1 -1 \,\right], & \text{falls}\; d_1 > 1 \\[4pt]\large \left[ \, 9\; d_3 \cdots d_k \cdots d_3\; 9 \, \right], & \text{falls}\; d_1 = 1 \; \text{und} \; d_2 = 0 \\[4pt]\large \left[ \, d_2\; d_3 \cdots d_k\; d_k \cdots d_3\; d_2 \,\right], & \text{falls}\; d_1 = 1 \; \text{und} \; d_2 > 0 \end{cases} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-f9ca429ff7b1bbeb993478eb79f68682_l3.png)
Beispiel 1: ![]() . Wir haben
. Wir haben ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() . Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Demzufolge bekommen wir die Ziffernfolge von
. Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Demzufolge bekommen wir die Ziffernfolge von ![]() zu
zu ![]() , also
, also ![]() .
.
Beispiel 2: ![]() . Wir haben
. Wir haben ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() . Nach der Fallunterscheidung trifft der zweite Fall zu. Nun erhalten wir die Ziffernfolge von
. Nach der Fallunterscheidung trifft der zweite Fall zu. Nun erhalten wir die Ziffernfolge von ![]() zu
zu ![]() , mithin
, mithin ![]() .
.
Beispiel 3: ![]() . Wir haben
. Wir haben ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() . Nach der Fallunterscheidung trifft der dritte Fall zu. Wir erhalten für die Ziffernfolge von
. Nach der Fallunterscheidung trifft der dritte Fall zu. Wir erhalten für die Ziffernfolge von ![]() demnach
demnach ![]() , und folglich
, und folglich ![]() .
.
2.4 Die Umkehrung der Palindromformel
Wir fragen nun umgekehrt: Welche Nummer trägt ein vorgegebenes dezimales Palindrom? Konkret: ![]() . Wie lautet das
. Wie lautet das ![]() , für das gilt:
, für das gilt: ![]() ?
?
Wegen ![]() und
und ![]() ist
ist ![]() größer als
größer als ![]() aber kleiner als
aber kleiner als ![]() . Für die genaue Bestimmung gehen wir zurück auf die vorstehend dargestellte anschauliche Palindromformel, aus welcher sich die algorithmische Vorschrift zur Berechnung unmittelbar ergibt.
. Für die genaue Bestimmung gehen wir zurück auf die vorstehend dargestellte anschauliche Palindromformel, aus welcher sich die algorithmische Vorschrift zur Berechnung unmittelbar ergibt.
Sei ![]() bzw.
bzw. ![]() die Ziffernfolge von
die Ziffernfolge von ![]() als
als ![]() -Tupel bzw. als
-Tupel bzw. als ![]() -Tupel und
-Tupel und ![]() die Ziffernfolge des gesuchten Wertes für
die Ziffernfolge des gesuchten Wertes für ![]() als
als ![]() -Tupel. Man bekommt die Ziffernfolge von
-Tupel. Man bekommt die Ziffernfolge von ![]() nach folgender Fallunterscheidung in sinngemäßer Umkehrung der Direktformel:
nach folgender Fallunterscheidung in sinngemäßer Umkehrung der Direktformel:
(17) ![Rendered by QuickLaTeX.com \begin{equation*} n = P_{10}^{-1}(p) \Leftrightarrow \begin{cases} \Large \left[\, p_1+1\; p_2\; p_3 \cdots p_k \,\right], &\text{falls}\; L(P) \bmod 2 = 1 \; \text{und}\; 0< p_1 < 9 \\[4pt]\Large \left[ \,1 \; 0 \; p_2 \;p_3 \cdots p_k \, \right], &\text{falls}\; L(P) \bmod 2 = 1 \; \text{und}\; p_1 = 9 \\[4pt] \Large \left[ \,1 \; p_1 \; p_2 \; p_3 \cdots p_k \, \right], &\text{falls}\; L(P) \bmod 2 = 0 \end{cases} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-c3d3b4084282b79686f258813d242050_l3.png)
Für die formale algorithmische Berechnung definieren wir ![]() und orientieren wir uns an den vorgenannten drei Fällen. Wenn
und orientieren wir uns an den vorgenannten drei Fällen. Wenn ![]() , das sind die beiden obigen Fälle mit
, das sind die beiden obigen Fälle mit ![]() , dann haben wir
, dann haben wir
(18) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} n = P_{10}^{-1}(P) &=10^{\frac{m}{2}} + \sum \limits_{k=0}^{\frac{m}{2}} \left(\left\lfloor \frac{P}{10^{k}}\right\rfloor \bmod 10\right) 10^{\frac{m}{2}-k} \\[8pt]&= \left\lfloor \frac{P}{10^{\frac{m}{2}}}\right\rfloor + 10^{\frac{m}{2}} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-fcf738e525c83fffdffb5b2466239a4a_l3.png)
Wie man sich leicht klar macht, muss man den Fall ![]() nicht separieren, weil sich der Summationsterm für den Index
nicht separieren, weil sich der Summationsterm für den Index ![]() , nämlich
, nämlich ![]() , mit dem Term vor der Summe zu
, mit dem Term vor der Summe zu ![]() ergänzt, so dass
ergänzt, so dass ![]() korrekterweise mit der Ziffernfolge
korrekterweise mit der Ziffernfolge ![]() beginnt. Für den obigen dritten Fall
beginnt. Für den obigen dritten Fall ![]() , der gleichbedeutend ist mit
, der gleichbedeutend ist mit ![]() , erhalten wir
, erhalten wir
(19) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} n = P_{10}^{-1}(P) &= 10^{\frac{m+1}{2}} + \sum \limits_{k=0}^{\frac{m-1}{2}} \left(\left\lfloor \frac{P}{10^{k}}\right\rfloor \bmod 10\right) 10^{\frac{m-1}{2}-k} \\[8pt]&= \left\lfloor \frac{P}{10^{\frac{m+1}{2}}}\right\rfloor + 10^{\frac{m+1}{2}} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-d906f56dff6f7189bf963f510a6c7e9c_l3.png)
Zusammen können wir dies in kompakter Form für alle ![]() und ohne Fallunterscheidung folgendermaßen schreiben:
und ohne Fallunterscheidung folgendermaßen schreiben:
(20) ![]()
Beispiel 1: ![]() . Wir haben
. Wir haben ![]() und
und ![]() . Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Demzufolge bekommen wir
. Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Demzufolge bekommen wir ![]() bzw.
bzw. ![]() .
.
Beispiel 2: ![]() . Wir haben
. Wir haben ![]() und
und ![]() . Nach der Fallunterscheidung trifft der zweite Fall zu. Nun erhalten wir
. Nach der Fallunterscheidung trifft der zweite Fall zu. Nun erhalten wir ![]() bzw.
bzw. ![]() .
.
Beispiel 3: ![]() . Wir haben
. Wir haben ![]() . Nach der Fallunterscheidung trifft der dritte Fall zu. Wir erhalten
. Nach der Fallunterscheidung trifft der dritte Fall zu. Wir erhalten ![]() bzw.
bzw. ![]() .
.
2.5 Die Anzahlfunktion für dezimale Palindrome
Aus den oben angegebenen Formeln über dezimale Palindrome für Vielfache von Zehnerpotenzen folgt direkt die Anzahl der Palindrome zwischen ![]() und
und ![]() zu
zu
(21) ![]()
Für die Anzahl der dezimalen Palindrome ![]() ,
, ![]() , ergibt sich daher nach Aufaddieren vorgenannter Partialsummen
, ergibt sich daher nach Aufaddieren vorgenannter Partialsummen
(22) ![Rendered by QuickLaTeX.com \begin{align*} A_{10}\left(10^{n}\right) &= \displaystyle \begin{cases} 2\cdot 10^{\frac{n}{2}} - 1, \; &n \bmod 2 = 0 \\[4pt]\displaystyle 11\cdot 10^{\frac{n-1}{2}} - 1, \; &n \bmod 2 = 1 \end{cases} \\[8pt] &= \displaystyle \frac{13 - 9\cdot (-1)^n}{2} \cdot 10^{\left\lfloor\frac{n}{2}\right\rfloor} - 1\end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-b2de278e6dbb3e7d3abee78638cf2f82_l3.png)
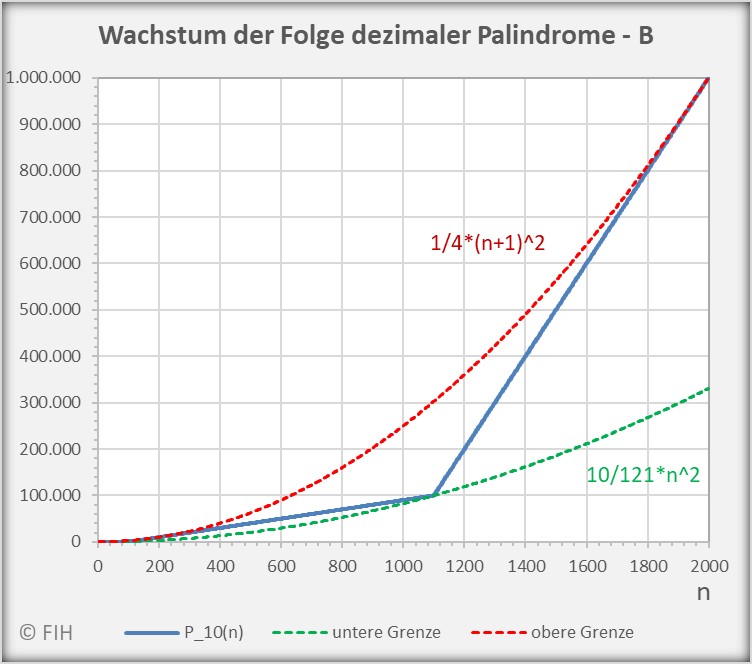
2.6 Das Wachstum der Folge dezimaler Palindrome
Dezimale Palindrome gehorchen für ![]() der Ungleichung
der Ungleichung
(23) ![]()
Die folgenden Abbildungen zeigen, wie die Folge der dezimalen Palindrome mit ![]() wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden (exemplarisch für
wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden (exemplarisch für ![]() bzw.
bzw. ![]() ).
).
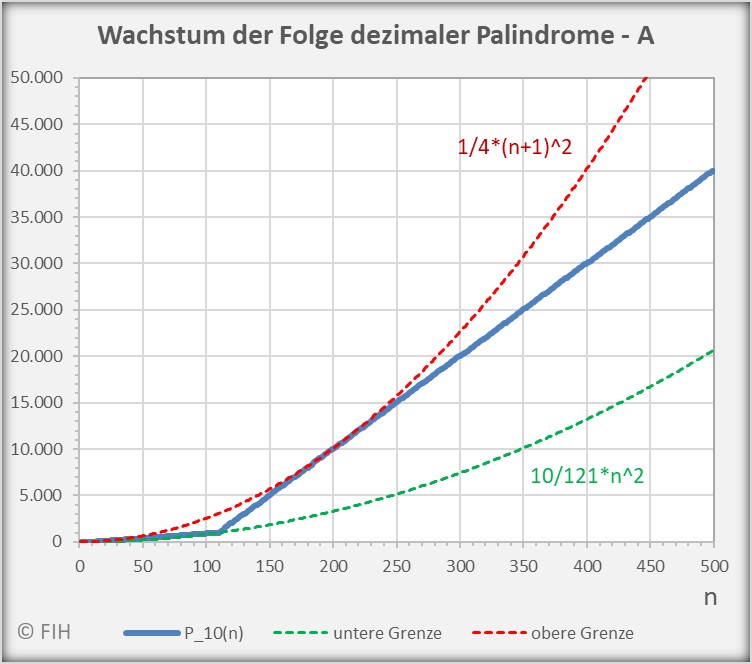
Beim Grenzübergang ![]() gilt
gilt
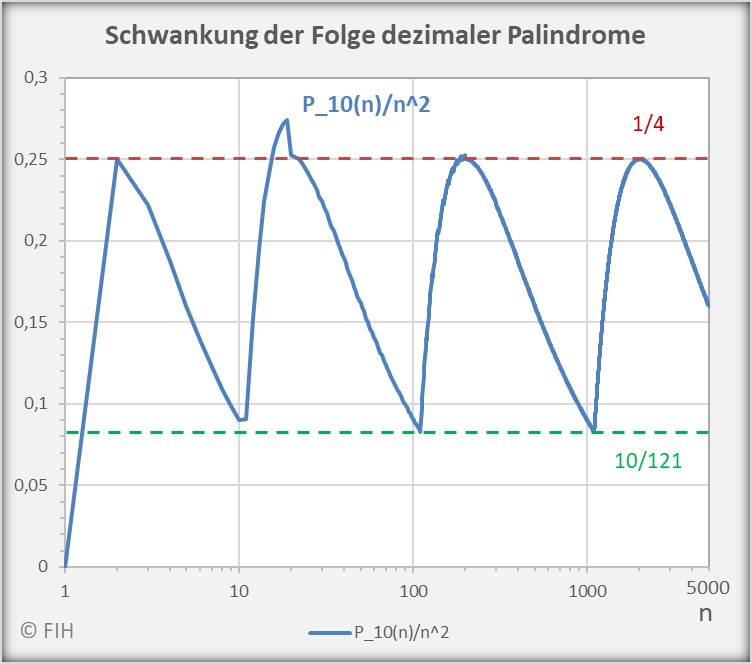
(24) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10}(n)}{n^2} &= \frac{10}{121} \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10}(n)}{n^2} &= \frac{1}{4} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-2000fd7595c01726355de5c483a5b786_l3.png)
Der Kurvenverlauf ![]() mit Bezug auf die Referenzkurve
mit Bezug auf die Referenzkurve ![]() ist für
ist für ![]() im nachfolgenden Diagramm mit den beiden Häufungspunkten bei
im nachfolgenden Diagramm mit den beiden Häufungspunkten bei ![]() und
und ![]() dargestellt. Im Unterschied zu oben ist die x-Achse hier logarithmisch skaliert.
dargestellt. Im Unterschied zu oben ist die x-Achse hier logarithmisch skaliert.
3 Dezimale Palindrome mit einer ungeraden Anzahl von Stellen
Wie man der Diskussion zu den dezimalen Palindromen entnimmt, gibt es prinzipiell zwei verschiedene Arten solcher Palindrome. Solche mit einer ungeraden Anzahl von Stellen und solche mit einer geraden Anzahl von Stellen. Beide haben unterschiedliche Charakteristika und gaben oben diversen Anlass zu Fallunterscheidungen.
Die ersten dezimalen Palindrome mit einer ungeraden Anzahl von Stellen sind:
(25) 
Wir benennen die Palindrome mit dem Formelzeichen ![]() .
.
Die ungeraden Palindrome mit der Nummer ![]() lauten daher
lauten daher ![]() . Für
. Für ![]() gilt dagegen
gilt dagegen ![]() . Die weitere Analyse ergibt die folgenden Beziehungen:
. Die weitere Analyse ergibt die folgenden Beziehungen:
(26) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array} {lll} P_{10\vert U}\left(d \cdot 10^q \right) &= (d-1) \cdot 10^{2q} + 9 \cdot 10^q + d - 1,\; &\text{für}\; 2 \le d \le 10 \\[8pt] P_{10\vert U}\left(d \cdot 10^q + 1\right) &= d \cdot 10^{2q} + d,\; &\text{für}\; 1 \le d \le 9 \\[8pt] P_{10\vert U}\left(d \cdot 10^q + j\right) &= d \cdot 10^{2q} + (j-1) \cdot 10^q+ d,\; &\text{für}\; 1 \le d \le 9, \; 1 \le j \le 10 \end{array} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-a49116c214c3bc2e84dd4ffbe8c023ee_l3.png)
3.1 Die rekursive Bestimmung
Man kann diese Palindrome ebenfalls rekursiv bestimmen. Der Algorithmus ist sogar einfacher als im allgemeinen Falle.
(27) ![]()
Damit können wir für ![]() das
das ![]() -te dezimale Palindrom mit einer ungeraden Anzahl von Stellen effizient berechnen.
-te dezimale Palindrom mit einer ungeraden Anzahl von Stellen effizient berechnen.
Die Parameter ![]() und
und ![]() sind dabei folgendermaßen zu bestimmen:
sind dabei folgendermaßen zu bestimmen:
(28) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} q &= 2\cdot \left\lfloor\log_{10}\left(n-1\right)\right\rfloor \\[4pt] d &= \left\lfloor \frac{n-1}{10^{\frac{q}{2}}} \right\rfloor \bmod 10 \\[4pt] m &= (n-1) \bmod 10^{\frac{q}{2}} + 1 \\[4pt]p &= \frac{q}{2} - \left\lfloor \log_{10}(\max(1,m-1)) \right\rfloor \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-853deb6772ea89d43af60c0376b033d0_l3.png)
Ein Rechenbeispiel für ![]() . Wie lautet das betreffende dezimale Palindrom mit einer ungeraden Anzahl von Stellen?
. Wie lautet das betreffende dezimale Palindrom mit einer ungeraden Anzahl von Stellen?
(29) 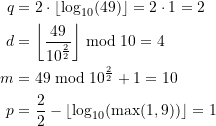
Eingesetzt in die Rekursionsformel erhalten wir
(30) 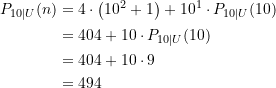
3.2 Die direkte Bestimmung
Für ![]() kann man mit der Definition
kann man mit der Definition ![]() das
das ![]() -te solche dezimale Palindrom folgendermaßen direkt berechnen:
-te solche dezimale Palindrom folgendermaßen direkt berechnen:
(31) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{10\vert U}(n) &= \sum \limits_{k=0}^{m-1} \left(\left\lfloor \frac{n-1}{10^{m-k}}\right\rfloor \bmod 10\right)\left(10^k + 10^{2m-k}\right) \;+ \\[4pt] & \quad \left((n-1) \bmod 10\right)\cdot 10^m \\[8pt]&= \sum \limits_{k=1}^{m-1} \left(\left\lfloor \frac{n-1}{10^{m-k}}\right\rfloor \bmod 10\right) \cdot 10^k \;+ \\[4pt] & \quad \left( n-1 \right) \cdot 10^m + \left\lfloor \frac{n-1}{10^{m}}\right\rfloor \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-3b6045f3a2909dad349cb40559ff8073_l3.png)
Auch hier ergibt sich eine anschauliche und leicht durchführbare Ableitung für die Berechnung des ![]() -ten solchen Palindroms. Sei
-ten solchen Palindroms. Sei ![]() die Ziffernfolge von
die Ziffernfolge von ![]() als
als ![]() -Tupel und
-Tupel und ![]() die Ziffernfolge des entsprechenden Palindroms
die Ziffernfolge des entsprechenden Palindroms ![]() als
als ![]() -Tupel. Man erhält das
-Tupel. Man erhält das ![]() -te Palindrom
-te Palindrom ![]() aus der Ziffernfolge von
aus der Ziffernfolge von ![]() nach der folgenden einfachen Vorschrift:
nach der folgenden einfachen Vorschrift:
(32) ![]()
Man beachte, dass hier ![]() und nicht
und nicht ![]() als Ausgangspunkt für die Zifferndarstellung herangezogen wird.
als Ausgangspunkt für die Zifferndarstellung herangezogen wird.
Beispiel: ![]() . Wir haben
. Wir haben ![]() , also
, also ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() . Demzufolge bekommen wir die Ziffernfolge von
. Demzufolge bekommen wir die Ziffernfolge von ![]() zu
zu ![]() , also
, also ![]() . Entsprechend ergibt sich die Summe in der Bestimmungsformel (31) zu
. Entsprechend ergibt sich die Summe in der Bestimmungsformel (31) zu ![]() und somit P_{10\vert U}(140) = 13900 + 30 + 1 = 13931\).
und somit P_{10\vert U}(140) = 13900 + 30 + 1 = 13931\).
3.3 Die Umkehrfunktion
Auch hier können wir fragen: Welche Nummer ![]() trägt ein vorgegebenes dezimales Palindrom
trägt ein vorgegebenes dezimales Palindrom ![]() mit einer ungeraden Anzahl von Stellen?
mit einer ungeraden Anzahl von Stellen?
Der Blick auf die dargestellte anschauliche Berechnungsvorschrift liefert sofort einen Ansatz für die Umkehrfunktion, da in der Ziffernfolge des Palindroms ![]() die Ziffernfolge von
die Ziffernfolge von ![]() enthalten ist. Mit
enthalten ist. Mit ![]() gilt
gilt
(33) ![]()
Da wir nur Palindrome mit einer ungeraden Anzahl von Stellen betrachten, gibt es stets eine gerade Zahl ![]() , so dass
, so dass ![]() . Nach Definition ist
. Nach Definition ist ![]() diese gerade Zahl, so dass der Exponent
diese gerade Zahl, so dass der Exponent ![]() in der Formel ganz ist.
in der Formel ganz ist.
3.4 Die Anzahlfunktion
Die Anzahl der Palindrome ![]() mit einer ungeraden Anzahl von Stellen zwischen
mit einer ungeraden Anzahl von Stellen zwischen ![]() und
und ![]() , genauer,
, genauer, ![]() , ist
, ist
(34) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} A_{10\vert U}(n)\left(10^{n}\right) - A_{10\vert U}(n)\left(10^{n-1}\right) &= \begin{cases} 0, &\text{falls} \; n \bmod 2 = 0 \\[4pt] \displaystyle 9\cdot 10^{\frac{n-1}{2}}, &\text{sonst} \end{cases} \\[8pt] &= \displaystyle 10^{ \left\lfloor\frac{n+1}{2}\right\rfloor} - 10^{ \left\lfloor\frac{n}{2}\right\rfloor} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-979260d66a9ce8da9ae01b07c74fda5c_l3.png)
Dies gilt für ![]() , die letzte Form auch für
, die letzte Form auch für ![]() . Für die Anzahl solcher Palindrome
. Für die Anzahl solcher Palindrome ![]() ,
, ![]() , folgt daher nach Aufaddieren vorgenannter Differenzen
, folgt daher nach Aufaddieren vorgenannter Differenzen
(35) ![]()
3.5 Das Wachstum der Folge
Für ![]() gilt die Ungleichung
gilt die Ungleichung
(36) ![]()
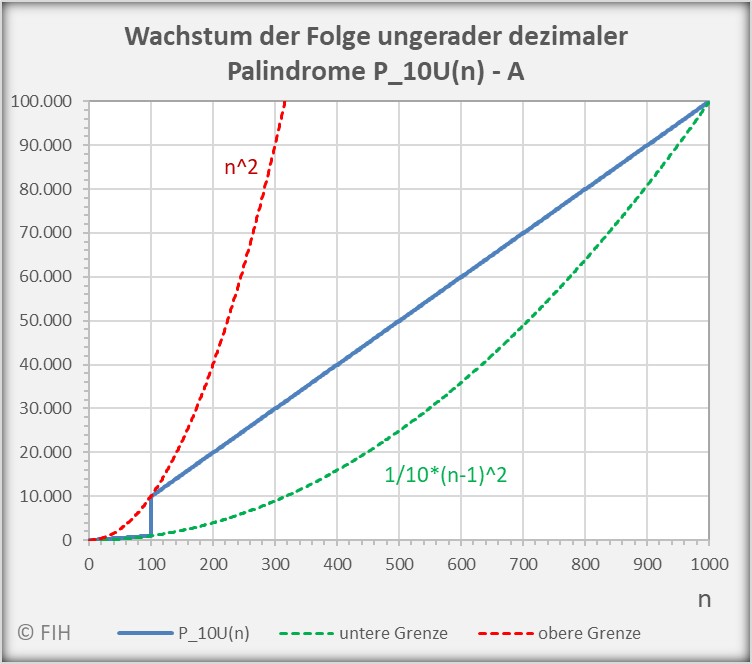
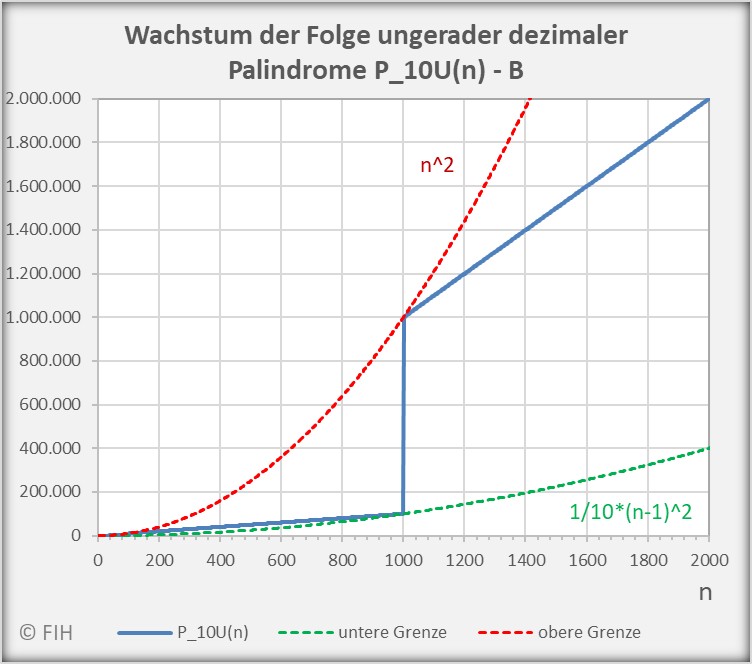
Den folgenden exemplarischen Abbildungen kann man für ![]() bzw.
bzw. ![]() entnehmen, wie die Folge der dezimalen Palindrome mit einer ungeraden Anzahl von Stellen mit
entnehmen, wie die Folge der dezimalen Palindrome mit einer ungeraden Anzahl von Stellen mit ![]() wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden.
wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden.
Beim Grenzübergang ![]() gilt
gilt
(37) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10\vert U}(n)}{n^2} &= \frac{1}{10} \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10\vert U}(n)}{n^2} &= 1 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-d9696926bca6efb291cdb49798cf472b_l3.png)
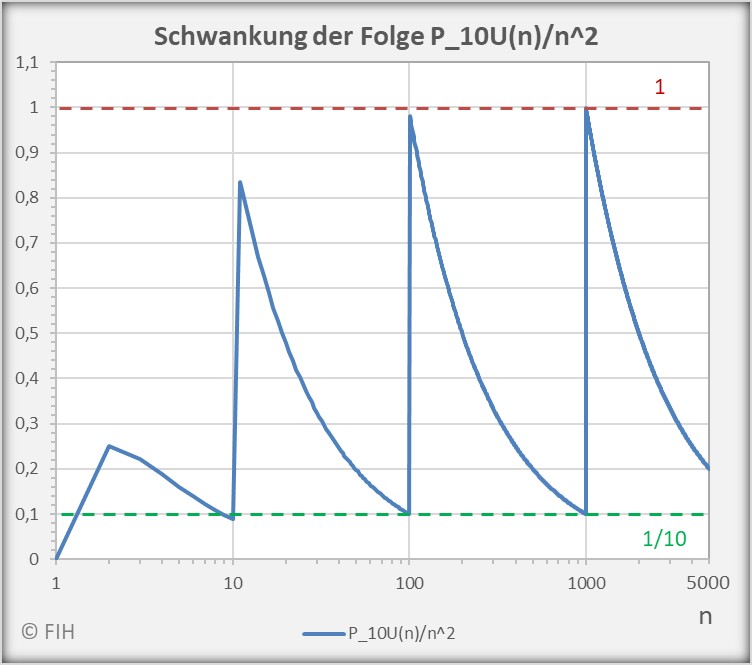
Zur Kurve des Quotienten ![]() für Werte
für Werte ![]() , s. das nachfolgende Diagramm (mit logarithmischer Skalierung der x-Achse) und den beiden Häufungspunkten
, s. das nachfolgende Diagramm (mit logarithmischer Skalierung der x-Achse) und den beiden Häufungspunkten ![]() und
und ![]() .
.
4 Dezimale Palindrome mit einer geraden Anzahl von Stellen
Die ersten dezimalen Palindrome mit einer geraden Anzahl von Stellen sind:
(38) 
Wir benennen diese Palindrome mit dem Formelzeichen ![]() .
.
Die solchermaßen definierten Palindrome mit der Nummer ![]() lauten daher
lauten daher ![]() . Für
. Für ![]() gilt dagegen
gilt dagegen ![]() . Die weitere Betrachtung zeigt:
. Die weitere Betrachtung zeigt:
(39) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array} {lll} P_{10\vert G}\left(d \cdot 10^q -1 \right) &= (d-1) \cdot 10^{2q+1} + 99\cdot 10^q + d - 1,\; &\text{für}\; 2 \le d \le 10 \\[8pt] P_{10\vert G}\left(d \cdot 10^q \right) &= d \cdot 10^{2q+1} + d,\; &\text{für}\; 1 \le d \le 9 \\[8pt] P_{10\vert G}\left(d \cdot 10^q + j\right) &= d \cdot 10^{2q+1} + 11 j \cdot 10^q+ d,\; &\text{für}\; 1 \le d \le 9, \; 1 \le j \le 9 \end{array} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-dce2fe9fbd40e49b54c6d1d13f9a87c8_l3.png)
4.1 Die rekursive Berechnung
Ähnlich wie oben kann man auch die Palindrome mit einer geraden Anzahl von Stellen mittels einer Rekursionsbeziehung ableiten.
(40) ![]()
Zusätzlich definieren wir ![]() . Damit können wir für
. Damit können wir für ![]() das
das ![]() -te solche Palindrom effizient bestimmen.
-te solche Palindrom effizient bestimmen.
Die Parameter ![]() und
und ![]() sind dabei folgendermaßen zu bestimmen:
sind dabei folgendermaßen zu bestimmen:
(41) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} q &= 2\cdot \left\lfloor\log_{10}(n)\right\rfloor + 1 \\[4pt] d &= \left\lfloor \frac{n}{10^{\frac{q-1}{2}}} \right\rfloor \bmod 10 \\[4pt]m &= n \bmod 10^{\frac{q-1}{2}} \\[4pt] p &= \frac{q-1}{2} - \left\lfloor \log_{10}(\max(1,m)) \right \rfloor \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-8584c5d2214ec76ddb6cb9016df97cc3_l3.png)
Ein Rechenbeispiel für ![]() . Wie lautet das betreffende dezimale Palindrom mit einer geraden Anzahl von Stellen?
. Wie lautet das betreffende dezimale Palindrom mit einer geraden Anzahl von Stellen?
(42) 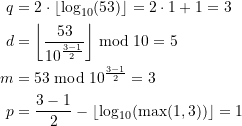
Eingesetzt in die Rekursionsformel erhalten wir
(43) 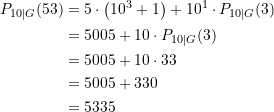
4.2 Die direkte Bestimmung
Für ![]() kann man mit Hilfe der Definition
kann man mit Hilfe der Definition ![]() das
das ![]() -te solche dezimale Palindrom folgendermaßen direkt berechnen:
-te solche dezimale Palindrom folgendermaßen direkt berechnen:
(44) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{10\vert G}(n) &= \sum \limits_{k=0}^{m} \left(\left\lfloor \frac{n}{10^{m-k}}\right\rfloor \bmod 10\right)\left(10^k + 10^{2m+1-k}\right) \\[8pt]&= \sum \limits_{k=0}^{m-1} \left(\left\lfloor \frac{n}{10^{m-k}}\right\rfloor \bmod 10\right) \cdot 10^k \; + \\[4pt] & \quad \; n \cdot 10^{m+1} + \left(n \bmod 10 \right) \cdot 10^m \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-7401feefb9c37fcd5e232abacb734d21_l3.png)
Die anschauliche Ableitung für die Berechnung des ![]() -ten Palindroms mit einer geraden Anzahl von Stellen verläuft ähnlich einfach wie im Falle der ungeraden Palindrome. Sei
-ten Palindroms mit einer geraden Anzahl von Stellen verläuft ähnlich einfach wie im Falle der ungeraden Palindrome. Sei ![]() die Ziffernfolge von
die Ziffernfolge von ![]() als
als ![]() -Tupel und
-Tupel und ![]() die Ziffernfolge des entsprechenden Palindroms
die Ziffernfolge des entsprechenden Palindroms ![]() als
als ![]() -Tupel. Das
-Tupel. Das ![]() -te Palindrom
-te Palindrom ![]() bestimmt man aus der Ziffernfolge von
bestimmt man aus der Ziffernfolge von ![]() nach folgender simplen Vorschrift:
nach folgender simplen Vorschrift:
(45) ![]()
Beispiel: ![]() . Wir haben
. Wir haben ![]() , also
, also ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() . Demzufolge bekommen wir die Ziffernfolge von
. Demzufolge bekommen wir die Ziffernfolge von ![]() zu
zu ![]() , also
, also ![]() . Entsprechend erhalten wir auf Basis der Direktformel mit
. Entsprechend erhalten wir auf Basis der Direktformel mit ![]() die beiden Terme des Summenausdrucks zu
die beiden Terme des Summenausdrucks zu ![]() und
und ![]() . Zusammen mit den äußeren Summanden ergibt sich
. Zusammen mit den äußeren Summanden ergibt sich ![]() .
.
4.3 Die Umkehrfunktion
Wir fragen analog: Welche Nummer ![]() trägt ein vorgegebenes dezimales Palindrom
trägt ein vorgegebenes dezimales Palindrom ![]() mit einer geraden Anzahl von Stellen?
mit einer geraden Anzahl von Stellen?
Auch hier liefert der Blick auf die dargestellte anschauliche Berechnungsvorschrift sofort einen Ansatz für die Umkehrfunktion, da in der Ziffernfolge des Palindroms ![]() die Ziffernfolge von
die Ziffernfolge von ![]() enthalten ist. Mit
enthalten ist. Mit ![]() gilt
gilt
(46) ![]()
Da nur Palindrome mit einer geraden Anzahl von Stellen betrachtet werden, gibt es stets eine ungerade Zahl ![]() , so dass
, so dass ![]() . Nach Definition ist
. Nach Definition ist ![]() diese ungerade Zahl, und somit der Exponent
diese ungerade Zahl, und somit der Exponent ![]() in der Formel eine ganze Zahl.
in der Formel eine ganze Zahl.
4.4 Die Anzahlfunktion
Die Anzahl der Palindrome ![]() mit einer geraden Anzahl von Stellen zwischen
mit einer geraden Anzahl von Stellen zwischen ![]() und
und ![]() ,
, ![]() , ist
, ist
(47) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} A_{10\vert G}\left(10^{n}\right) - A_{10\vert G})\left(10^{n-1}\right) &= \begin{cases} \displaystyle 9\cdot 10^{\frac{n-2}{2}}, &\text{falls} \; n \bmod 2 = 0 \\[4pt] 0, &\text{sonst} \end{cases} \\[8pt] &= \displaystyle 10^{ \left\lfloor\frac{n}{2}\right\rfloor} - 10^{ \left\lfloor\frac{n-1}{2}\right\rfloor} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-390202f5499fe286c63fdf83c0c9a73d_l3.png)
Für die Anzahl solcher Palindrome ![]() ,
, ![]() , folgt daher nach Aufaddieren vorgenannter Differenzen
, folgt daher nach Aufaddieren vorgenannter Differenzen
(48) ![]()
4.5 Das Wachstum der Folge
Für ![]() gilt die Ungleichung
gilt die Ungleichung
(49) ![]()
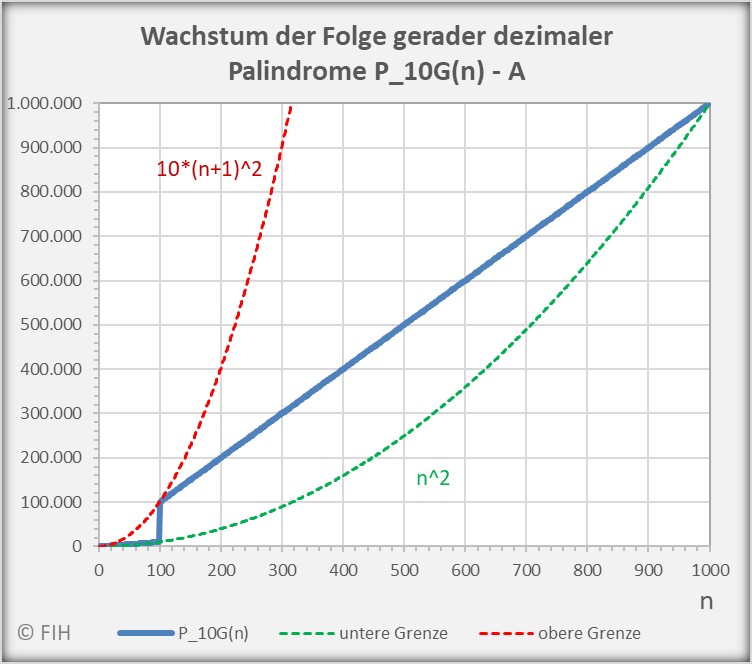
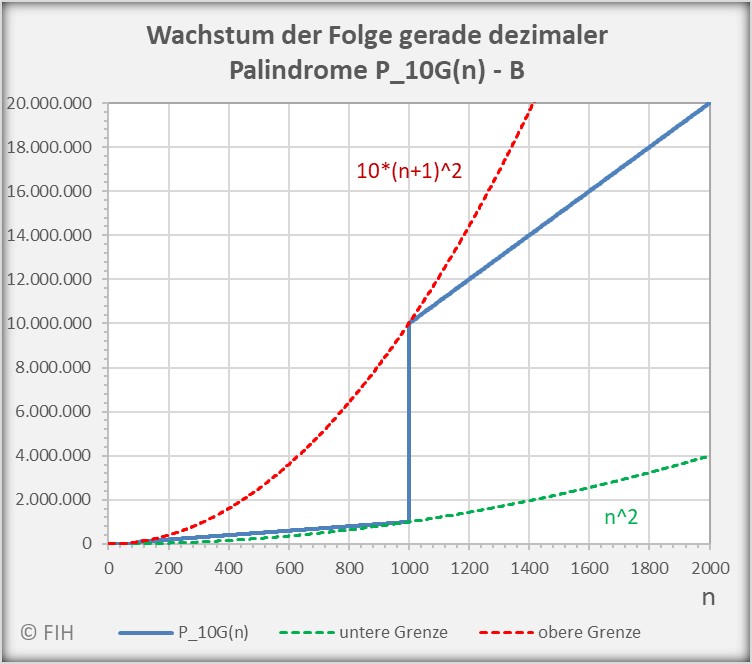
Den beiden nachfolgenden Abbildungen kann man für ![]() bzw.
bzw. ![]() entnehmen, wie die Folge der dezimalen Palindrome mit einer geraden Anzahl von Stellen mit
entnehmen, wie die Folge der dezimalen Palindrome mit einer geraden Anzahl von Stellen mit ![]() wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden.
wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden.
Beim Grenzübergang ![]() gilt
gilt
(50) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10\vert G}(n)}{n^2} &= 1 \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10\vert G}(n)}{n^2} &= 10 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-232673df86f2179c608eee722eea8df4_l3.png)
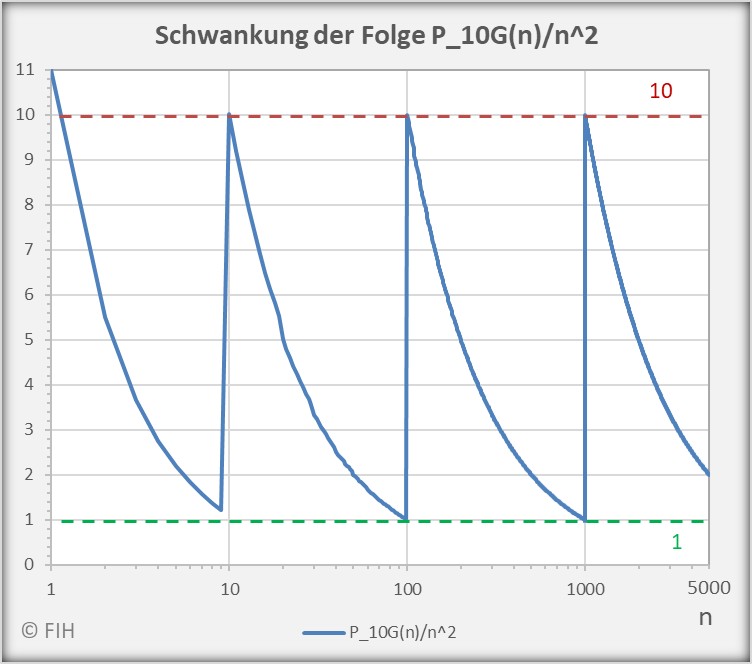
Der Kurvenverlauf der Folge ![]() ist im nachfolgenden Diagramm mit den beiden Häufungspunkten
ist im nachfolgenden Diagramm mit den beiden Häufungspunkten ![]() und
und ![]() beispielhaft für
beispielhaft für ![]() in logarithmischer Skalierung dargestellt.
in logarithmischer Skalierung dargestellt.
5 Der Zusammenhang zwischen der Folge der ungeraden, geraden und allgemeinen dezimalen Palindromen
Jedes dezimale Palindrom mit einer ungeraden oder einer geraden Anzahl von Stellen ist auch ein allgemeines dezimales Palindrom, allerdings zu einem anderen Index ![]() . Umgekehrt hat natürlich jedes dezimale Palindrome entweder einer ungerade oder eine gerade Anzahl von Stellen. In diesem Falle stellt sich jeweils die Frage, für welchen Index
. Umgekehrt hat natürlich jedes dezimale Palindrome entweder einer ungerade oder eine gerade Anzahl von Stellen. In diesem Falle stellt sich jeweils die Frage, für welchen Index ![]() ? Da ein dezimales Palindrom genau dann gerade ist, wenn
? Da ein dezimales Palindrom genau dann gerade ist, wenn ![]() , können wir die Zuordnung einfach auf Basis dieser Fallunterscheidung treffen, wobei
, können wir die Zuordnung einfach auf Basis dieser Fallunterscheidung treffen, wobei ![]() und
und ![]() .
.
(51) ![Rendered by QuickLaTeX.com \begin{equation*} P_{10}(n) = \begin{cases} P_{10\vert U})\left(n + 1 - 10^{\lambda(n)}\right), &\text{wenn} \; \lambda(n) = \overline{\lambda}(n) \\[8pt]P_{10\vert G}\left(n - 10^{\lambda(n)}\right), &\text{sonst} \end{cases} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-d68091156d9bdb14b324df62d29a818c_l3.png)
In der anderen Richtung ergeben sich die beiden Beziehungen
(52) ![Rendered by QuickLaTeX.com \begin{align*} P_{10\vert U}(n)) &= P_{10}\left(n - 1 + 10^{\displaystyle \left \lfloor \log_{10}(\max(1,n-1))\right \rfloor} \right) \\[8pt]P_{10\vert G}(n) &= P_{10}\left(n + 10^{\displaystyle \left \lfloor \log_{10}(n)\right \rfloor + 1} \right) \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-1b8e2baf9971e274ffcc0f7fa3877f38_l3.png)
Interessant sind noch eine Reihe von Grenzwerten, die die zwar ähnlichen, aber doch unterschiedlichen Verläufe der Folgen ![]() ,
, ![]() und
und ![]() mit ihren definierten Sprüngen deutlich machen. Es gilt
mit ihren definierten Sprüngen deutlich machen. Es gilt
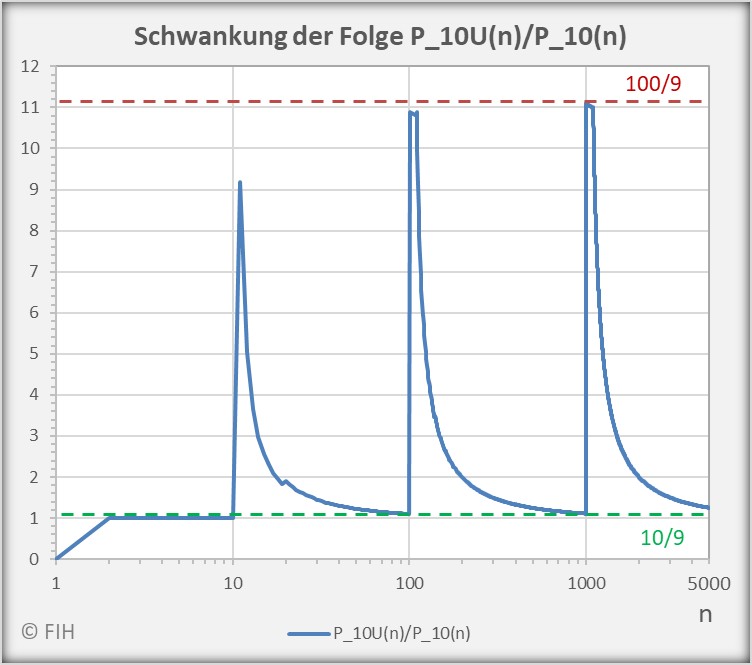
(53) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10\vert U}(n)}{P_{10}(n)} &= \frac{10}{9} \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10\vert U}(n)}{P_{10}(n)} &= \frac{100}{9} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-452f5f1dfa700b3ff16ec1b0221c4257_l3.png)
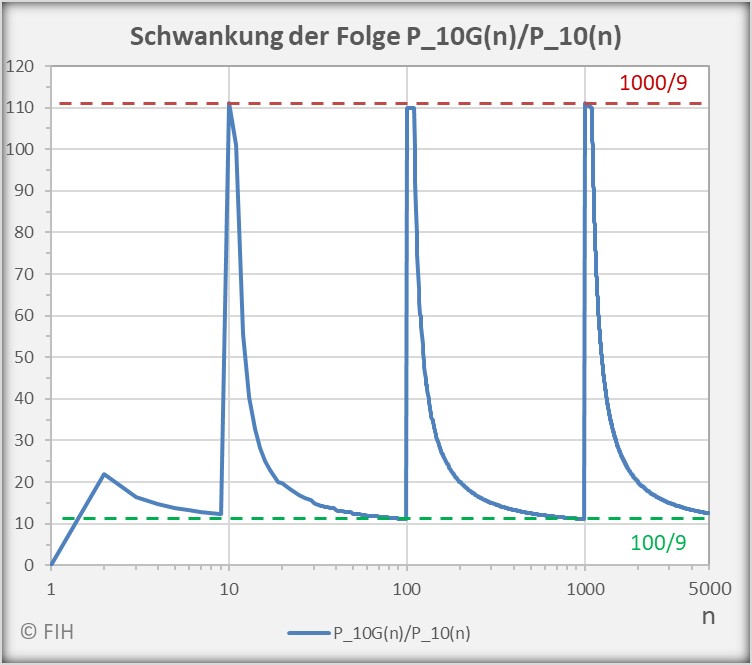
(54) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10\vert G}(n)}{P_{10}(n)} &= \frac{100}{9} \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10\vert G}(n)}{P_{10}(n)} &= \frac{1000}{9} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-8bdb7be2857b16f4234f4a1927f852c8_l3.png)
Die beiden Grafiken zeigen exemplarisch die Kurvenverläufe der Quotientenfolgen ![]() und
und ![]() bis
bis ![]() . Die jeweiligen unteren und oberen Grenzwerte (Häufungspunkte
. Die jeweiligen unteren und oberen Grenzwerte (Häufungspunkte ![]() und
und ![]() ) können ebenfalls entnommen werden.
) können ebenfalls entnommen werden.
Wenn ![]() eine Zehnerpotenz
eine Zehnerpotenz ![]() ist, dann macht die Folge der Palindrome
ist, dann macht die Folge der Palindrome ![]() einen Sprung. Die Höhe des Sprungs entnimmt man den beiden folgenden Grenzwerten.
einen Sprung. Die Höhe des Sprungs entnimmt man den beiden folgenden Grenzwerten.
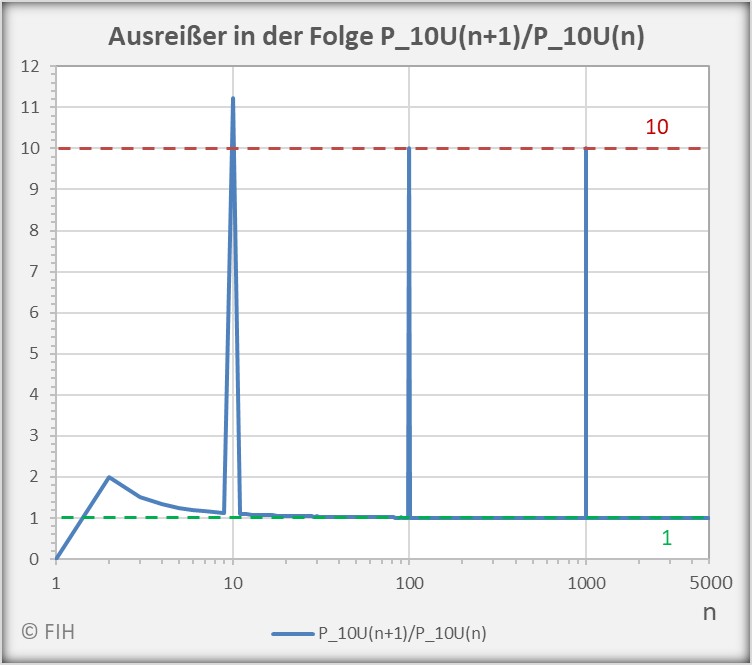
(55) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10\vert U}(n+1)}{P_{10\vert U}(n)} &= 1 \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10\vert U}(n+1)}{P_{10\vert U}(n)} &= 10 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-5b9f4bab7010664bd71bfbc26e17869c_l3.png)
Ähnlich macht auch die Folge der Palindrome ![]() einen Sprung, allerdings schon einen Term vorher, also genau bei der Zehnerpotenz.
einen Sprung, allerdings schon einen Term vorher, also genau bei der Zehnerpotenz.
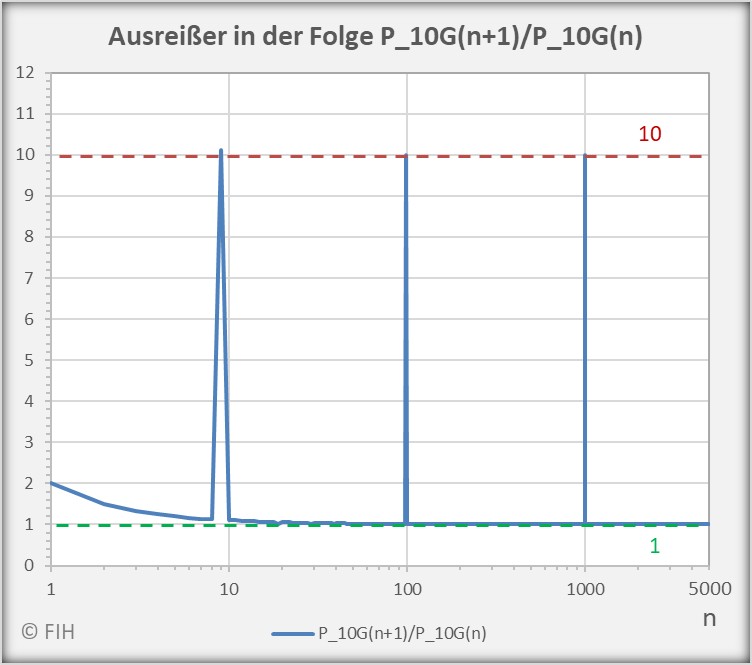
(56) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10\vert G}(n+1)}{P_{10\vert G}(n)} &= 1 \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10\vert G}(n+1)}{P_{10\vert G}(n)} &= 10 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-52fd2ead8e1501cc9194b40d07fd4735_l3.png)
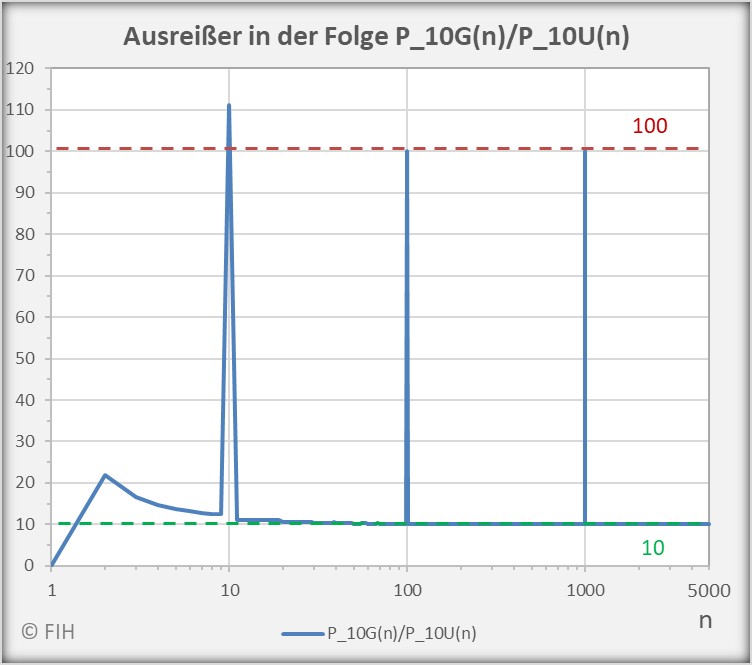
Die genannten Sprünge der beiden Quotientenfolgen ![]() und
und ![]() werden in den untenstehenden Diagrammen für
werden in den untenstehenden Diagrammen für ![]() anschaulich gemacht. Die Ausreißer nach oben häufen sich bei
anschaulich gemacht. Die Ausreißer nach oben häufen sich bei ![]() . Nach unten bildet sich jeweils ein Häufungspunkt bei
. Nach unten bildet sich jeweils ein Häufungspunkt bei ![]() .
.
Beim Vergleich der Palindrome mit einer ungeraden Anzahl von Stellen ![]() mit den Palindromen
mit den Palindromen ![]() fällt auf, dass Letztere offenbar schneller wachsen als Erstere.
fällt auf, dass Letztere offenbar schneller wachsen als Erstere.
(57) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_{10\vert G}(n)}{P_{10\vert U}(n)} &= 10 \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_{10\vert G}(n)}{P_{10\vert U}(n)} &= 100 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-50729a28ca9018b4dae7dfccc6d32e9a_l3.png)
Tatsächlich ist ![]() asymptotisch 10-mal größer als
asymptotisch 10-mal größer als ![]() . Im Gegensatz zu den oben betrachteten Fällen, wo die Quotienten stets in einem weiten Bereich von etwa 1:10 oder 10:100 schwanken oder sich sprunghaft ändern, ist die Folge der Quotienten
. Im Gegensatz zu den oben betrachteten Fällen, wo die Quotienten stets in einem weiten Bereich von etwa 1:10 oder 10:100 schwanken oder sich sprunghaft ändern, ist die Folge der Quotienten ![]() konvergent mit dem Grenzwert
konvergent mit dem Grenzwert ![]() . Dies erkennt man auf Basis der folgenden Überlegung:
. Dies erkennt man auf Basis der folgenden Überlegung:
(58) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{10\vert G}(n)&= 10 \cdot \left(P_{10\vert U}(n+1) - P_{10\vert U}(n+1) \bmod 10^{m} \right) \;+ \\[4pt] & \quad \left\lfloor\frac{P_{10\vert U}(n+1)}{10^{m}}\right\rfloor \bmod 10 \cdot 10^{m} + P_{10\vert U}(n+1) \bmod 10^{m} \\[8pt] &= 10 \cdot P_{10\vert U}(n+1) + \left\lfloor\frac{P_{10\vert U}(n+1)}{10^{m}}\right\rfloor \bmod 10 \cdot 10^{m} \;- \\[4pt] & \quad \quad 9 \cdot P_{10\vert U}(n+1) \bmod 10^{m} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-634ec29e4c47ca5c52427c27ad171fff_l3.png)
woraus folgt
(59) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \frac{P_{10\vert G}(n)}{P_{10\vert U}(n+1)}&= 10 + \frac{\left\lfloor\frac{P_{10\vert U}(n+1)}{10^{m}}\right\rfloor \bmod 10 \cdot 10^{m} - 9\cdot P_{10\vert U}(n+1) \bmod 10^{m}}{P_{10\vert U}(n+1)} \\[8pt] &= 10 + O\left(10^{-m}\right) \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-6098dc6049623c092f2e2f6b2c9d061a_l3.png)
Dabei haben wir ![]() und
und ![]() berücksichtigt. Es gilt demnach
berücksichtigt. Es gilt demnach
(60) ![]()
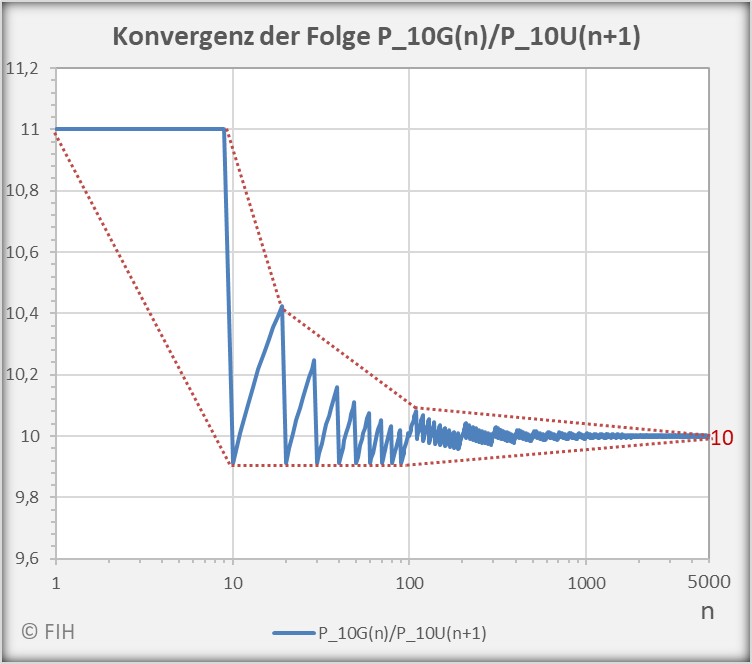
Das nachfolgend dargestellte Diagramm zeigt bespielhaft den Konvergenzverlauf der Folge ![]() in Kontrast zur Divergenz von
in Kontrast zur Divergenz von ![]() für Werte
für Werte ![]() . Der Grenzwert (Grafik Konvergenz:
. Der Grenzwert (Grafik Konvergenz: ![]() ) sowie der obere und untere Häufungspunkt (Grafik Ausreißer:
) sowie der obere und untere Häufungspunkt (Grafik Ausreißer: ![]() und
und ![]() ) sind eingetragen.
) sind eingetragen.
6 Binäre Palindrome
Im Folgenden betrachten wir die Zahlen im Binärsystem (nur die Ziffern ![]() und
und ![]() ). Nichtsdestotrotz schreibt man die Zahlen dezimal, so sind wir es gewohnt. Z.B. ist die Nummer 17 in dieser Folge die Zahl
). Nichtsdestotrotz schreibt man die Zahlen dezimal, so sind wir es gewohnt. Z.B. ist die Nummer 17 in dieser Folge die Zahl ![]() . Die ersten aufeinanderfolgenden binären Palindrome sind:
. Die ersten aufeinanderfolgenden binären Palindrome sind: ![]() … (s. The On-Line Encyclopedia of Integer Sequences, Link: https://oeis.org/A006995 [Numbers whose binary expansion is palindromic] für weitere Zahlen).
… (s. The On-Line Encyclopedia of Integer Sequences, Link: https://oeis.org/A006995 [Numbers whose binary expansion is palindromic] für weitere Zahlen).
In der nachfolgenden Tabelle sind die ersten 32 binären Palindrome in binärer und dezimaler Darstellung aufgelistet.
– binär – | – dezimal – | |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 1 |
| 3 | 11 | 3 |
| 4 | 101 | 5 |
| 5 | 111 | 7 |
| 6 | 1001 | 9 |
| 7 | 1111 | 15 |
| 8 | 10001 | 17 |
| 9 | 10101 | 21 |
| 10 | 11011 | 27 |
| 11 | 11111 | 31 |
| 12 | 100001 | 33 |
| 13 | 101101 | 45 |
| 14 | 110011 | 51 |
| 15 | 111111 | 63 |
| 16 | 1000001 | 65 |
| 17 | 1001001 | 73 |
| 18 | 1010101 | 85 |
| 19 | 1011101 | 93 |
| 20 | 1100011 | 99 |
| 21 | 1101011 | 107 |
| 22 | 1110111 | 119 |
| 23 | 1111111 | 127 |
| 24 | 10000001 | 129 |
| 25 | 10011001 | 153 |
| 26 | 10100101 | 165 |
| 27 | 10111101 | 189 |
| 28 | 11000011 | 195 |
| 29 | 11011011 | 219 |
| 30 | 11100111 | 231 |
| 31 | 11111111 | 255 |
| 32 | 100000001 | 257 |
Man kann das ![]() -te binäre Palindrom bestimmen, ohne alle in Frage kommenden Zahlen im Einzelnen betrachten zu müssen. Z.B. ist das 1000ste binäre Palindrom die Zahl
-te binäre Palindrom bestimmen, ohne alle in Frage kommenden Zahlen im Einzelnen betrachten zu müssen. Z.B. ist das 1000ste binäre Palindrom die Zahl ![]() , das 10-milliardste binäre Palindrom ist
, das 10-milliardste binäre Palindrom ist ![]() . Im letzteren Falle hat die entsprechende Binärzahl bereits 65 Stellen. Eine ganz einfache allgemeine Formel für das
. Im letzteren Falle hat die entsprechende Binärzahl bereits 65 Stellen. Eine ganz einfache allgemeine Formel für das ![]() -te binäre Palindrom – wir bezeichnen es im Folgenden kurz mit
-te binäre Palindrom – wir bezeichnen es im Folgenden kurz mit ![]() – gibt es nicht, doch kann man in speziellen Fällen das
– gibt es nicht, doch kann man in speziellen Fällen das ![]() -te binäre Palindrom leicht berechnen, z.B. gilt
-te binäre Palindrom leicht berechnen, z.B. gilt
(61) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{lcl} P_2 (2^m - 1) &=&2^{2m-2}-1 \\[4pt] P_2 (2^m) &=&2^{2m-2}+1 \\[4pt] P_2 ( 2^m+1) &=&2^{2m-2}+2^{m-1}+1 \\[4pt]P_2( 5\cdot 2^{m-2}-1) &=&2^{2m-2}+2^{m-3}-3 \\[4pt] P_2 ( 5\cdot 2^{m-2}) &=&2^{2m-2}+2^{m-3}+3 \\[4pt]P_2 ( 6\cdot 2^{m-2}-1 ) &=&2^{2m-1}-1 \\[4pt] P_2 ( 6\cdot 2^{m-2} ) &=&2^{2m-1}+1 \\[4pt] P_2( 6\cdot 2^{m-2}+1 ) &=&2^{2m-1}+2^{m}+2^{m-1}+1 \\[4pt]P_2 ( 7\cdot 2^{m-2}-1 ) &=&2^{2m-1}+2^{m-2}-3 \\[4pt]P_2 ( 7\cdot 2^{m-2} ) &=&2^{2m-1}+2^{m-2}+3 \end {array} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-3ace8bc4d632c03768e13f66cd3a0f37_l3.png)
Demnach ist also ![]() das 1025ste binäre Palindrom. Die unmittelbar vorhergehenden 1024sten und 1023sten Palindrome sind
das 1025ste binäre Palindrom. Die unmittelbar vorhergehenden 1024sten und 1023sten Palindrome sind ![]() und
und ![]() .
.
6.1 Rekursive Berechnung
Für die allgemeine Bestimmung kann man eine rekursive Berechnungsmethode anwenden:
(62) ![]()
wobei ![]() und die Parameter
und die Parameter ![]() folgendermaßen bestimmt werden:
folgendermaßen bestimmt werden:
6.2 Direkte Berechnung
Eine Möglichkeit zur direkten Bestimmung des ![]() -ten binären Palindroms ist die Folgende (für
-ten binären Palindroms ist die Folgende (für ![]() ):
):
(63) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_2\left( n \right)=&\,2^{2m-1-p}+1+p\cdot (1-{{\left( {-1} \right)}^{n}})\cdot {{2}^{m-2}} \\[4pt]&+\,\sum \limits_{{k=1}}^{m-1-p} {\left( {\dfrac{{n-\left( {3-p} \right)\cdot {2^{m-1}}}}{2^{m-1-k}}\bmod~2} \right) \left( {2^k+{2^{2m-1-p-k}}} \right)} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-03ee87eea3abe2ddd19b40e1960d1ace_l3.png)
Wobei ![]() und
und ![]() oder, was das gleiche bedeutet, der Parameter nach folgender Fallunterscheidung eingesetzt wird:
oder, was das gleiche bedeutet, der Parameter nach folgender Fallunterscheidung eingesetzt wird:
Hiermit berechnete binäre Palindrome sind in der nachfolgenden Tabelle aufgelistet.
Hierzu noch einige Bitmuster:
– binär – | – dezimal – | |
|---|---|---|
| 50 | 1001001001 | 585 |
| 100 | 100100001001 | 2313 |
| 200 | 10010000001001 | 9225 |
| 300 | 101011000110101 | 22069 |
| 400 | 1001000000001001 | 36873 |
| 500 | 1111010000101111 | 62511 |
| 600 | 10101100000110101 | 88117 |
| 700 | 11011110001111011 | 113787 |
| 800 | 100100000000001001 | 147465 |
| 900 | 110000100001000011 | 198723 |
| 1000 | 111101000000101111 | 249903 |
| 1500 | 1111011100011101111 | 506095 |
| 2000 | 11110100000000101111 | 999471 |
| 5000 | 10111000100000100011101 | 6045981 |
| 10000 | 1011100010000000100011101 | 24183069 |
| 100000 | 10000110101000000000010101100001 | 2258634081 |
6.3 Wachstum der Folge binärer Palindrome
Binäre Palindrome gehorchen für ![]() der Ungleichung
der Ungleichung
(64) ![]()
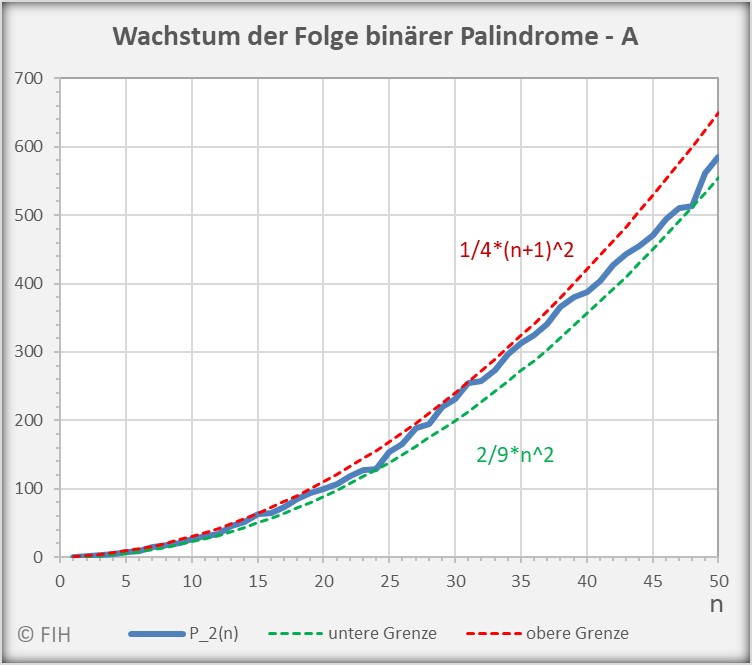
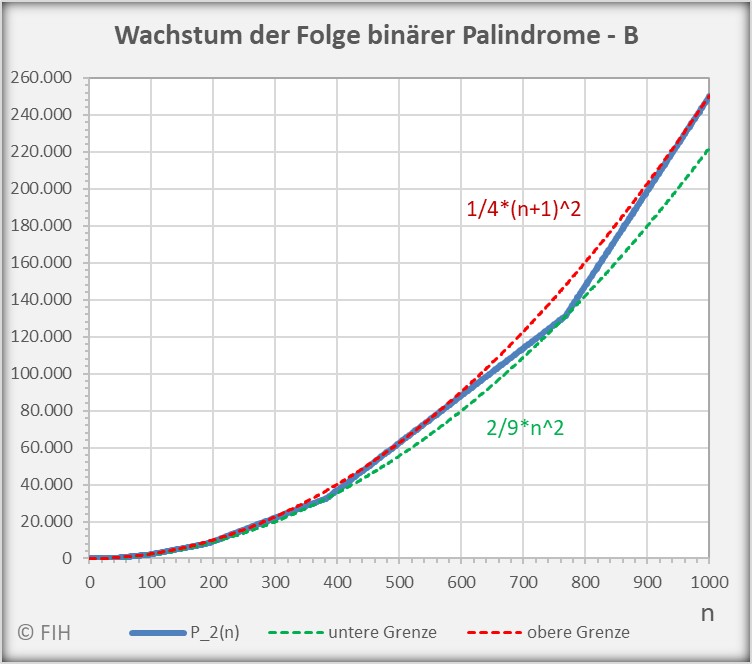
Den folgenden Diagrammen kann man für ![]() bzw.
bzw. ![]() beispielhaft entnehmen, wie die Folge der binären Palindrome mit
beispielhaft entnehmen, wie die Folge der binären Palindrome mit ![]() wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden.
wächst und wie die Folgenglieder durch die Ungleichung begrenzt werden.
Beim Grenzübergang ![]() gilt
gilt
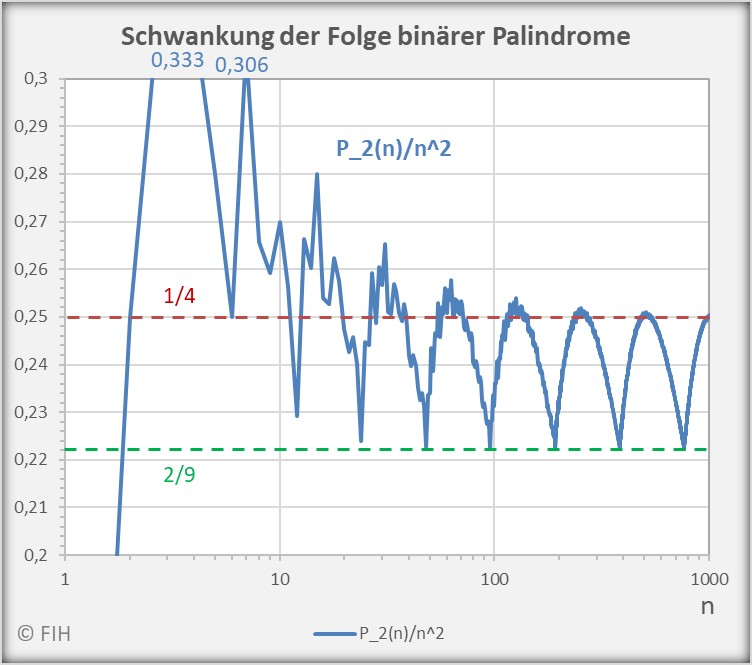
(65) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_2(n)}{n^2} = \frac{2}{9} \\[8pt] \limsup_{n \rightarrow \infty} \frac{P_2(n)}{n^2} = \frac{1}{4} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-9559ab6b5e38c13d177f5f076584e2f7_l3.png)
Der Kurvenverlauf der Folge ![]() ist im nachfolgenden Diagramm für
ist im nachfolgenden Diagramm für ![]() exemplarisch dargestellt. Der obere und der untere Häufungspunkt,
exemplarisch dargestellt. Der obere und der untere Häufungspunkt, ![]() und
und ![]() , sind entsprechend eingetragen.
, sind entsprechend eingetragen.
6.4 Differenzen von binären Palindromen
Die Differenzen aufeinander folgender Palindrome bilden eine interessante Folge:
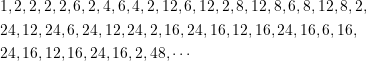
(s. The On-Line Encyclopedia of Integer Sequences, Link: https://oeis.org/A164126). Die ![]() und die
und die ![]() treten dabei unendlich oft als Folgenglieder auf. Bezeichnen wir die Glieder mit
treten dabei unendlich oft als Folgenglieder auf. Bezeichnen wir die Glieder mit ![]() so gilt ab
so gilt ab ![]()
(66) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \Delta {{P}_{2}}\left( {4\cdot {{2}^{m}}-1} \right)&=2 \\[4pt] \Delta {{P}_{2}}\left( {6\cdot {{2}^{m}}-1} \right)&=2 \\[4pt] \Delta {{P}_{2}}\left( {7\cdot {{2}^{m}}-1} \right)&=6 \\[4pt] \Delta {{P}_{2}}\left( {5\cdot {{2}^{m}}-1} \right)&=6,\; \text{für}\; m \ge 1\end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-e2b44212d7fd89b0afb52155a03220f4_l3.png)
Die allgemeine Formel für ![]() lässt sich aus der obigen Formel für
lässt sich aus der obigen Formel für ![]() ableiten. Mit den Definitionen
ableiten. Mit den Definitionen ![]() und
und ![]() sowie
sowie
(67) ![]()
ergibt sich
(68) 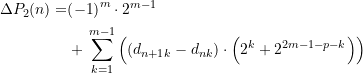
sofern ![]() oder
oder ![]() . In den beiden Sonderfällen
. In den beiden Sonderfällen ![]() und
und ![]() ist
ist ![]() .
.
Die Folge lässt sich auch rekursiv berechnen (wie stets, ![]() gesetzt)
gesetzt)
(69) ![Rendered by QuickLaTeX.com \begin{align*} {\Delta P_2 (n)= \left\{ \begin{array}{lrcl} 2\cdot \Delta P_2\ (n-2^{m-1}) \text{,} &2^{m}\le n&<&2^{m}+2^{m-2}-1 \\[4pt] 6, &n&=&2^{m}+2^{m-2}-1 \\[4pt] \Delta P_2 (n-2^{m-2}) \text{,} &2^{m}+2^{m-2}\le n&<&2^{m}+2^{m-1}-1 \\[4pt] 2, &n&=&2^m+2^{m-1}-1 \\[4pt] ( 2+(-1)^n)\cdot \Delta P_2 (n-2^{m-1})\text{,} &2^m+2^{m-1}\le n&<&2^{m+1} \end{array} \right. } \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-e8755be6f8791af5857b6ade404097d5_l3.png)
Die Rekursionsbeziehung gilt ab ![]() , die Bezugswerte für
, die Bezugswerte für ![]() sind
sind ![]() . Der folgenden Umschreibung kann man unmittelbar entnehmen, wie sich nachfolgende Glieder aus den vorhergehenden bestimmen lassen.
. Der folgenden Umschreibung kann man unmittelbar entnehmen, wie sich nachfolgende Glieder aus den vorhergehenden bestimmen lassen.
(70) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \Delta {{P}_{2}}\left( {{{2}^{m}}-1+{{2}^{{m-1}}}+k} \right)&=\left( {2-{{{\left( {-1} \right)}}^{k}}} \right) \Delta {{P}_{2}}\left( {{{2}^{m}}-1+k} \right) \quad \text{für }0\le k\le {{2}^{{m-1}}} \\[4pt] \Delta {{P}_{2}}\left( {{{2}^{m}}+k} \right)&=2\cdot \Delta {{P}_{2}}\left( {{{2}^{{m-1}}}+k} \right) \quad \text{für }0\le k<{{2}^{{m-2}}}-2 \\[4pt] \Delta {{P}_{2}}\left( {{{2}^{m}}+{{2}^{{m-2}}}+k} \right)&=\Delta {{P}_{2}}\left( {{{2}^{m}}+k} \right) \quad \text{für }0\le k<{{2}^{{m-2}}}-2 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-5f7b6df3de9853b099e46eed37123a7a_l3.png)
Wenn man ab einer Stelle ![]() jeweils die nächsten
jeweils die nächsten ![]() Folgenglieder nebeneinander schreibt, so sieht man, dass ein symmetrisches Muster entsteht. Für
Folgenglieder nebeneinander schreibt, so sieht man, dass ein symmetrisches Muster entsteht. Für ![]() ergibt sich zum Beispiel das Tupel
ergibt sich zum Beispiel das Tupel ![]() . Mit anderen Worten: Die Folge der Differenzen der binären Palindrome bildet ihrerseits wieder symmetrische Muster. Tatsächlich gilt allgemein
. Mit anderen Worten: Die Folge der Differenzen der binären Palindrome bildet ihrerseits wieder symmetrische Muster. Tatsächlich gilt allgemein
(71) ![]()
Wegen ![]() für
für ![]() oder
oder ![]() sowie
sowie ![]() für
für ![]() , werden diese symmetrischen Muster jeweils durch eine
, werden diese symmetrischen Muster jeweils durch eine ![]() links und rechts begrenzt und haben stets die
links und rechts begrenzt und haben stets die ![]() als zentrales Element.
als zentrales Element.
Und weil nach obiger Formel die Folgenglieder mit ![]() direkt aus den Gliedern mit
direkt aus den Gliedern mit ![]() bestimmt werden, ergibt sich gleichfalls für
bestimmt werden, ergibt sich gleichfalls für ![]()
(72) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \Delta {{P}_{2}}\left( {{{2}^{m}}-1+{{2}^{{m-1}}}+k} \right)&=\left( {2-{{{\left( {-1} \right)}}^{k}}} \right)\cdot \Delta {{P}_{2}}\left( {{{2}^{m}}-1+k} \right) \\[4pt] &=\left( {2-{{{\left( {-1} \right)}}^{k}}} \right)\cdot \Delta {{P}_{2}}\left( {{{2}^{m}}-1+{{2}^{{m-1}}}-k} \right) \\[4pt] &=\Delta {{P}_{2}}\left( {{{2}^{m}}-1+{{2}^{{m-1}}}+{{2}^{{m-1}}}-k} \right) \\[4pt] &=\Delta {{P}_{2}}\left( {{{2}^{{m+1}}}-1-k} \right) \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-8ab2abbceb0ddba0f5bf30a99589d2f5_l3.png)
Demnach bilden auch die Zahlen ab ![]() mit den folgenden
mit den folgenden ![]() Gliedern symmetrische Muster von
Gliedern symmetrische Muster von ![]() Elementen, begrenzt mit je einer
Elementen, begrenzt mit je einer ![]() sowie der
sowie der ![]() in der Mitte. Das entsprechende symmetrische Tupel für
in der Mitte. Das entsprechende symmetrische Tupel für ![]() lautet
lautet ![]() .
.
Wenn man die Folge nach den symmetrischen Mustern ordnet und untereinanderschreibt, erkennt man, dass das ![]() -te Folgenglied auch einfacher berechnet werden kann.
-te Folgenglied auch einfacher berechnet werden kann.
| Folgenglieder | |
| Folgenglieder | |
| 0 | – |
| 0 | |
| 1 | |
| 1 | |
| 2 | |
| 2 | |
| 3 | |
| 3 | |
| 4 | |
| 4 | |
| 5 | |
| 5 |
Es ergibt sich die folgende Darstellung:
(73) ![Rendered by QuickLaTeX.com \begin{align*} \Delta P_2 (n)= \left\{ \begin{array}{lll} 2\text{,} &n=2^{m+1}-1\text{, oder } &n=3\cdot 2^{m-1}-1 \\[4pt] 2^{m-1}\text{,} &n=2^{m}+2k\text{, } &0\le k<2^{m-2} \\[4pt] 3\cdot 2^{m-2}\text{,} &n=2^{m}-1+(2k+1)2^1\text{, } &0\le k<2^{m-2} \\[4pt] 3\cdot 2^{m-3}\text{,} &n=2^{m}-1+(2k+1)2^2\text{, } &0\le k<2^{m-3} \\[4pt] 3\cdot 2^{m-4}\text{,} &n=2^{m}-1+(2k+1)2^3\text{, } &0\le k<2^{m-4} \\ \vdots &\vdots &\vdots \\ 3\cdot 2^{1}\text{,} &n=2^{m}-1+(2k+1)2^{m-2}\text{, } &0\le k<2^{1} \\[4pt] 3\cdot 2^{m-1}\text{,} &n=3\cdot 2^{m-1}+2k \text{, } &0\le k<2^{m-2} \end{array} \right. \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-e40b38dbc3dc7cbed90a73c37e8ee6e8_l3.png)
Kompakter geschrieben folgt daraus
(74) ![Rendered by QuickLaTeX.com \begin{align*} \Delta P_2 (n)= \left\{ \begin{array}{llll} 2\text{,} &n=2^{m+1}-1\text{, oder } &n=3\cdot 2^{m-1}-1 \\[4pt] 2^{m-1}\text{,} &n=2^{m}+2k\text{, } &0\le k<2^{m-2} \\[4pt] 3\cdot 2^{m-1-j}\text{,} &n=2^{m}-1+(2k+1)2^j\text{, } &0\le k<2^{m-1-j}\text{, } \\ &&1\le j<m-1 \\[4pt] 3\cdot 2^{m-1}\text{,} &n=3\cdot 2^{m-1}+2k \text{, } &0\le k<2^{m-2} \\ \end{array} \right. \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-fad182b5d0cb0ed6d16f050700dd0441_l3.png)
Das kann man weiter vereinfachen zu
(75) ![Rendered by QuickLaTeX.com \begin{align*} \Delta P_2 (n)= \left\{ \begin{array}{cl} 2\text{,} &n+1 \in \left\{2^{m+1}\text{, } 3\cdot 2^{m-1}\right\} \\[4pt] 2^{m-1}\text{,} &n\equiv 0 {\pmod 2} \land n<3\cdot 2^{m-1} \\[4pt] 3\cdot 2^{m-1}\text{,} &n\equiv 0 {\pmod 2} \land n \ge 3\cdot 2^{m-1} \\[4pt] \dfrac{3\cdot 2^{m-1}}{\text{ggt}\left( {{n+1-2^{m}}{,2^{m}}} \right)} \text{, } &\text{sonst} \end{array} \right. \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-842162974f630c139b433dd7c6c34362_l3.png)
Dabei steht ![]() für die Funktion, die den größten gemeinsamen Teiler von
für die Funktion, die den größten gemeinsamen Teiler von ![]() und
und ![]() berechnet.
berechnet.
Eine noch etwas kompaktere Form ist die Folgende
(76) ![Rendered by QuickLaTeX.com \begin{align*} \Delta P_2 (n)= \left\{ \begin{array}{cl} 2\text{,} &n+1 \in \left\{2^{m+1}\text{, } 3\cdot 2^{m-1}\right\} \\[4pt] \dfrac{\left({2 - {\left( -1 \right)}^{n-(n-1){\left\lfloor {\frac{2n}{3\cdot 2^m}}\right\rfloor} }} \right) \cdot 2^{m-1}}{\text{ggt}\left( {{n+1-2^{m}}{,2^{m}}} \right)} \text{, } &\text{sonst} \end{array} \right. \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-3445d93a9f74a2099549c33d08d334b4_l3.png)
6.5 Alternative Formel für die direkte Berechnung
Kehren wir zurück zur Folge der Palindrome. Für die obige Formel zur Berechnung es ![]() -ten binären Palindroms
-ten binären Palindroms ![]() bekommen wir wegen
bekommen wir wegen
(77) ![]()
nun eine Alternative auf Basis der Differenzenfolge. Man erhält mit ![]()
(78) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle {P_2} (n) = &\,2^{2m-2}+1+2\left\lfloor {\frac{{n-{{2}^{m}}}}{{{{2}^{{m-1}}}}}} \right\rfloor \\[4pt] & \,+{{2}^{{m-1}}}\left\lfloor {\frac{1}{2}\min \left( {n+1-{{2}^{m}}{{{,2}}^{{m-1}}}+1} \right)} \right\rfloor \\[4pt] & \,+3\cdot {{2}^{{m-1}}}\left\lfloor {\frac{1}{2}\max \left( {n+1-3\cdot {{2}^{{m-1}}},0} \right)} \right\rfloor \\[4pt] & \,+3\cdot \sum\limits_{{j=2}}^{{m-1}}{{\left( {\left\lfloor {\dfrac{{n+{{2}^{{j-1}}}-{{2}^{m}}}}{{{{2}^{j}}}}} \right\rfloor \cdot {{2}^{{m-j}}}} \right)}} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-88904bb5d3e42025dbc84e275259b4f2_l3.png)
6.6 Ein anschauliches Verfahren zur Bestimmung binärer Palindrome
In Anlehnung an das Vorgehen bezüglicher dezimaler Palindrome ergibt sich auch hier eine anschauliche Möglichkeit zur Bestimmung des einem Index ![]() zugeordneten binären Palindroms. Sei
zugeordneten binären Palindroms. Sei ![]() das Bitmuster von
das Bitmuster von ![]() mit
mit ![]() Stellen und
Stellen und ![]() die resultierende Bitfolge des entsprechenden Palindroms
die resultierende Bitfolge des entsprechenden Palindroms ![]() mit einer unbekannten Anzahl von
mit einer unbekannten Anzahl von ![]() Stellen. Man erhält das
Stellen. Man erhält das ![]() -te binäre Palindrom
-te binäre Palindrom ![]() aus dem Bitmuster von
aus dem Bitmuster von ![]() nach folgender einfacher Berechnungsvorschrift:
nach folgender einfacher Berechnungsvorschrift:
(79) ![Rendered by QuickLaTeX.com \begin{equation*} P_{2}(n) \Leftrightarrow \begin{cases} \large \left[\,1 \; d_3\; d_4 \cdots d_k \cdots d_4\; d_3\; 1 \,\right], & \text{wenn}\; d_2 = 0 \\[8pt]\large \left[\,1 \; d_3 \; d_4 \cdots d_k\; d_k \cdots d_4\; d_3 \; 1 \, \right], & \text{sonst} \end{cases} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-2618f92a8214d59c9c17d761e59007de_l3.png)
Im ersteren Falle der Unterscheidung ist ![]() ein binäres Palindrom mit einer ungeraden Anzahl von Stellen und es ergibt sich
ein binäres Palindrom mit einer ungeraden Anzahl von Stellen und es ergibt sich ![]() , im zweiten Falle hat das Palindrom eine gerade Anzahl von Stellen und es gilt
, im zweiten Falle hat das Palindrom eine gerade Anzahl von Stellen und es gilt ![]() .
.
Beispiel 1: ![]() . Es trifft der erste Fall zu mit
. Es trifft der erste Fall zu mit ![]() ,
, ![]() ,
, ![]() und
und ![]() . Wir erhalten das Bitmuster von
. Wir erhalten das Bitmuster von ![]() zu
zu ![]() , also
, also ![]() , und es gilt
, und es gilt ![]() .
.
Beispiel 2: ![]() . Es trifft der zweite Fall zu mit
. Es trifft der zweite Fall zu mit ![]() ,
, ![]() ,
, ![]() und
und ![]() . Wir erhalten das Bitmuster von
. Wir erhalten das Bitmuster von ![]() zu
zu ![]() , also
, also ![]() , und es gilt
, und es gilt ![]() .
.
6.7 Die Umkehrung der binären Palindromformel
Ist ![]() ein vorgegebenes binäres Palindrom, so stellt sich die Frage, das Wievielte in der geordneten Folge der Palindrome es ist. Die Antwort darauf gibt dieser Abschnitt. Für
ein vorgegebenes binäres Palindrom, so stellt sich die Frage, das Wievielte in der geordneten Folge der Palindrome es ist. Die Antwort darauf gibt dieser Abschnitt. Für ![]() gilt mit
gilt mit ![]() :
:
(80) 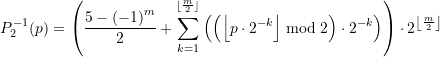
Das kann man wegen ![]() für
für ![]() umformen zu
umformen zu
(81) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{2}^{{-1}}(p)=&\,\left( {5-{{{\left( {-1} \right)}}^{m}}} \right)\cdot {{2}^{{\left\lfloor {\frac{m}{2}} \right\rfloor -1}}}-3\cdot \sum\limits_{{k=2}}^{{^{{\left\lfloor {\frac{m}{2}} \right\rfloor }}}}{{\left\lfloor {\dfrac{p}{{{{2}^{k}}}}} \right\rfloor \cdot {{2}^{{\left\lfloor {\frac{m}{2}} \right\rfloor -k}}}}} \\[4pt] &\,+\left( {\left\lfloor {\dfrac{p}{2}} \right\rfloor \cdot {{2}^{{\left\lfloor {\frac{m}{2}} \right\rfloor -1}}}-2\cdot \left\lfloor {\dfrac{p}{2}\cdot {{2}^{{^{{-\left\lfloor {\frac{m}{2}} \right\rfloor }}}}}} \right\rfloor } \right)\cdot \left\lfloor {\dfrac{{m-1}}{m}+\dfrac{1}{2}} \right\rfloor \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-f594c3b8b2cdc4999322554f71241d2a_l3.png)
Zwei andere Schreibweisen ergeben sich mittels der Ersetzung ![]()
(82) 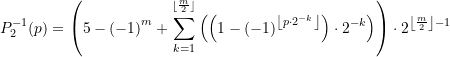
(83) 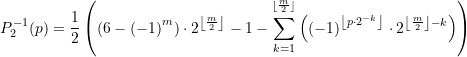
Die obige Umkehrungsformel (80) funktioniert, weil der entsprechende Indexparameter ![]() im Bitmuster des resultierenden binären Palindroms enthalten ist. Das hatten wir auch schon bei der Darstellung der anschaulichen Berechnungsvorschrift zur Bestimmung binärer Palindrome gesehen (s. Abschnitt 6.6). Ausgehend davon erkennt man bei genauer Auswertung, dass sich die Umkehrungsformel mit dem komplexen Summenausdruck deutlich vereinfachen lässt. Tatsächlich erhalten wir
im Bitmuster des resultierenden binären Palindroms enthalten ist. Das hatten wir auch schon bei der Darstellung der anschaulichen Berechnungsvorschrift zur Bestimmung binärer Palindrome gesehen (s. Abschnitt 6.6). Ausgehend davon erkennt man bei genauer Auswertung, dass sich die Umkehrungsformel mit dem komplexen Summenausdruck deutlich vereinfachen lässt. Tatsächlich erhalten wir
(84) ![]()
Daraus folgt z.B., dass ![]() das 1954-ste binäre Palindrom ist.
das 1954-ste binäre Palindrom ist.
6.8 Das größte binäre Palindrom zu einer vorgegebenen Zahl
Wenn eine beliebige natürliche Zahl ![]() vorgegeben ist, wie bestimmt sich dann das größte binäre Palindrom kleiner oder gleich
vorgegeben ist, wie bestimmt sich dann das größte binäre Palindrom kleiner oder gleich ![]() ? Die Antwort gibt die folgende Formel in Verbindung mit der Tabelle:
? Die Antwort gibt die folgende Formel in Verbindung mit der Tabelle:
(85) ![]()
Wie man sieht, gilt für die hier definierte Funktion ![]()
(86) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \text{F}\left( {p,m} \right) &= \left\lfloor {\frac{p}{{{{2}^{q}}}}} \right\rfloor \cdot {{2}^{q}}+\operatorname{Reversal}\left( p \right)\ \bmod {{2}^{q}} \\[4pt]\displaystyle \text{F}\left( {p-{{2}^{q}},s} \right) &=\left\lfloor {\frac{{p-{{2}^{q}}}}{{{{2}^{q}}}}} \right\rfloor \cdot {{2}^{q}}+\operatorname{Reversal}\left( {p-{{2}^{q}}} \right)\ \bmod {{2}^{q}} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-3a558c277d9432701201846f3388c7ba_l3.png)
Dabei steht ![]() für die Umkehrung des Bitmusters von
für die Umkehrung des Bitmusters von ![]() .
.
6.9 Die Anzahl binärer Palindrome
Weiter kann man nun fragen, wie viele Palindrome ![]() es gibt und wie groß die Summe dieser Palindrome ist. Die Anzahl der Palindrome zwischen
es gibt und wie groß die Summe dieser Palindrome ist. Die Anzahl der Palindrome zwischen ![]() und
und ![]() kann man leicht bestimmen. Es gilt (für
kann man leicht bestimmen. Es gilt (für ![]() )
)
(87) ![]()
Damit berechnet man die Anzahl der Palindrome ![]() für
für ![]() zu
zu
(88) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} {{A}_{2}}({{2}^{n}})&=\sum\limits_{{0\le {{P}_{2}}(k)<{{2}^{n}}}}{1} \\[8pt]&=\left\{ \begin{array}{ll} {2\cdot 2^{\frac{n}{2}}-1} \text{, } &n\equiv 0 {\pmod 2} \\[4pt] {3\cdot 2^{\frac{n-1}{2}}-1} \text{, } &n\equiv 1 {\pmod 2} \end{array} \right. \\[8pt] &=\dfrac{{5-{{{\left( {-1} \right)}}^{n}}}}{2}\cdot {{2}^{{\left\lfloor {\frac{n}{2}} \right\rfloor }}}-1 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-f0a629eef8c5af32ab3ce176f840550c_l3.png)
6.10 Die Summe binärer Palindrome
Die Summe der Palindrome zwischen ![]() und
und ![]() ergibt sich ferner für
ergibt sich ferner für ![]() zu
zu
(89) ![]()
Und schließlich erhalten wir damit die Summe der Palindrome ![]() für
für ![]() zu
zu
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle {{S}_{2}}({{2}^{n}}) &= \sum\limits_{{0\le {{P}_{2}}(k)<{{2}^{n}}}}^{{}}{{{{P}_{2}}(k)}} \\[8pt] &=1+\left\{ \begin{array}{ll} 15\cdot \dfrac{8^{\frac{n-2}{2}}-1}{7}+3\cdot {8^{\frac{n-2}{2}}} \text{, } &n\equiv 0 {\pmod 2} \\[4pt] 15\cdot \dfrac{8^{\frac{n-1}{2}}-1}{7} \text{, } &n\equiv 1 {\pmod 2} \end{array} \right. \\[8pt]&=\dfrac{8}{7} \cdot \left\{ \begin{array}{ll} \dfrac{9}{16}\cdot {2^{3\frac{n}{2}}}-1 \text{, } \quad \quad \quad &n\equiv 0 {\pmod 2} \\[4pt] \dfrac{{15}}{8}\cdot {{2}^{{3\frac{{n-1}}{2}}}}-1 \text{, } \quad \quad \quad &n\equiv 1 {\pmod 2} \end{array} \right \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-e2b79598d27c31096610d780d426ea61_l3.png)
Mithin
(90) ![]()
Weitaus komplizierter ist die Formel für die Summe der binären Palindrome, die kleiner oder gleich einem vorgegebenen Palindrom ![]() sind. Die folgende Formel gilt für binäre Palindrome , wobei
sind. Die folgende Formel gilt für binäre Palindrome , wobei ![]()
(91) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \sum\limits_{0\le {P_2}(k)\le p}^{}{{P_2}(k)}=&\,\sum\limits_{{0 \le {P_2}(k)<{2^n}}}^{}{{P_2}(k)}+\left( {\left\lfloor {p\cdot {2^{{-\left\lfloor {\frac{m}{2}} \right\rfloor }}}} \right\rfloor \bmod 2} \right)\cdot p\, \\[4pt] &\,+{2^m}+1+\sum\limits_{k=1}^{{\left\lfloor {\frac{m}{2}} \right\rfloor -1}}{{\left( {\left\lfloor {\dfrac{p}{2^k}} \right\rfloor \bmod 2} \right)\cdot {R_ {{m(p)}{k}}(p)}}} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-842f014374f6b3132f55d381296362a9_l3.png)
wobei ![]() definiert ist als
definiert ist als
(92) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} {R_ {{m(p)}{k}}(p)}=&\, {2^k}+{2^{m-k}}+\sum\limits_{j=0}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k}}{{{s_{m-2k-2j-1}}{2^{k+j+1}}}} \\[4pt] &\, +\left( {\left\lfloor {p\cdot {{2}^{{-\left\lfloor {\frac{m}{2}} \right\rfloor }}}} \right\rfloor \bmod 2} \right) \cdot \left( {\sum\limits_{j=0}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k}}{{{a_{m-2k-2j-1}}}}} \right) \cdot \sum\limits_{j=0}^{k-1} \left( {{2^j}+{2^{m-j}}} \right) \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-b52d4eb5aa0741ea75db02b304a427eb_l3.png)
sowie ![]() und
und ![]() folgendermaßen
folgendermaßen
(93) ![Rendered by QuickLaTeX.com \begin{align*} {{s}_{m}}=&\sum\limits_{{ 2^{m-1} \le {{P}_{2}}(k)<{{2}^{m}}}}^{{}}{{{{P}_{2}}(k)}}=\frac{3}{8}\cdot {{2}^{{m+\left\lfloor {\frac{{m+1}}{2}} \right\rfloor }}} \\[4pt] {{a}_{m}}=&\sum\limits_{{ 2^{m-1} \le {{P}_{2}}(k)<{{2}^{m}}}}^{{}}{1}={{2}^{{\left\lfloor {\frac{{m-1}}{2}} \right\rfloor }}} \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-96c4cb900c6aa1fcf31557157527755e_l3.png)
gesetzt sind. Die entsprechenden Summenausdrücke über ![]() und
und ![]() in der Definition von
in der Definition von ![]() kann man auswerten und findet
kann man auswerten und findet
(94) ![Rendered by QuickLaTeX.com \begin{align*} &\sum\limits_{{j=0}}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k}}{{{{s}_{{m-2k-2j-1}}}}}{{2}^{{k+j+1}}}=\,{{2}^{{m-\left\lfloor {\tfrac{m}{2}} \right\rfloor +1}}}\left( {{{4}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k-1}}}-1} \right)+\left( {2-{{{\left( {-1} \right)}}^{m}}} \right) {{2}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor}}} \\[4pt] &\sum\limits_{{j=0}}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k}}{{{{a}_{{m-2k-2j-1}}}}}=\,{{2}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k}}} \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-289fd0c69932a97b84d8cb62ffee5ee9_l3.png)
Damit erhält man
(95) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} {R_{{m(p)}{k}}(p)}=&\, {{2}^{k}}+{{2}^{{m-k}}}+{{2}^{{m-\left\lfloor {\tfrac{m}{2}} \right\rfloor +1}}}\left( {{{4}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k-1}}}-1} \right) + \left( {2-{{{\left( {-1} \right)}}^{m}}} \right) {{2}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor}}} \\[4pt] &\,+{{2}^{{\left\lfloor {\tfrac{m}{2}} \right\rfloor -k}}}\left( {p-\left\lfloor {\left( {p\bmod {{2}^{{m-k+1}}}} \right)\cdot {{2}^{{-k}}}} \right\rfloor \cdot {{2}^{k}}} \right) \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-1b3fc1610bf5e06ca23f586c44951e83_l3.png)
und es ergibt sich schließlich die Summenformel
(96) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \sum\limits_{{0\le {{P}_{2}}\left( k \right)\le p}}^{{}}{{{{P}_{2}}(k)}}=&\,\dfrac{8}{7}\cdot \left( {\dfrac{3}{4}\cdot \dfrac{{4-{{{\left( {-1} \right)}}^{m}}}}{{3+{{{\left( {-1} \right)}}^{m}}}}\cdot {{2}^{{3\left\lfloor {\frac{m}{2}} \right\rfloor }}}-1} \right) \\[4pt]&\,+\left( {\left\lfloor {p\cdot {{2}^{{-\left\lfloor {\frac{m}{2}} \right\rfloor }}}} \right\rfloor \bmod 2} \right)\cdot p+{{2}^{m}}+1 \\[4pt]&\,+\sum\limits_{{k=1}}^{{\left\lfloor {\frac{m}{2}} \right\rfloor -1}}{{\left( {\left\lfloor {\dfrac{p}{{{{2}^{k}}}}} \right\rfloor \bmod 2} \right)\cdot {R_{{m(p)}{k}}(p)} }} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-84c131bb17e508987585b24570ed6236_l3.png)
Will man die Summe der Palindrome bis zu einem bestimmten Index bestimmen, also
(97) ![]()
so muss man zunächst ![]() berechnen und kann dann die vorstehende Formel anwenden.
berechnen und kann dann die vorstehende Formel anwenden.
7 Palindrome mit beliebigen Basen
Palindrome in beliebigen Basen ![]() können ähnlich wie die diskutierten Fälle von dezimalen, Basis
können ähnlich wie die diskutierten Fälle von dezimalen, Basis ![]() , und binären, Basis
, und binären, Basis ![]() , Palindromen behandelt werden. Wir präsentieren die betreffenden Formeln ohne auf die nähere Ableitung einzugehen.
, Palindromen behandelt werden. Wir präsentieren die betreffenden Formeln ohne auf die nähere Ableitung einzugehen.
Es gelten die Zusammenhänge
(98) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array} {lll} P_{b}(2 \cdot b^q - 1) &= b^{2q} - 1, &\text{für}\; q \ge 0 \\[8pt] P_{b}(2 \cdot b^q) &= b^{2q} + 1, &\text{für}\; q > 0 \\[8pt]P_{b}(b^q + b^{q-1}) &= b^{2q-1} + 1, &\text{für}\; q > 0 \\[8pt]P_{b}(b^q + b^{q-1} - 1) &= b^{2q-1} - 1, &\text{für}\; q > 0 \\[8pt]P_{b}((d+1) \cdot b^q) &= d \cdot b^{2q} +d, &\text{für}\; 0 < d < b, \, q \ge 0 \\[8pt] P_{b}((d+b) \cdot b^{q-1}) &= d \cdot b^{2q-1} + d, &\text{für}\; 0 < d < b, \, q > 0 \end{array} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-f0b65ecb8ab9eb8e14edff08edcfdccc_l3.png)
Es gibt einen direkten Zusammenhang zwischen bestimmten Wertebereichen von ![]() und der Stellenanzahl des zugeordneten Basis-
und der Stellenanzahl des zugeordneten Basis-![]() -Palindroms. Diese Stellenanzahl ist von Bedeutung, weil sie den Charakter der Symmetrieeigenschaft des Palindroms unmittelbar beeinflusst. Bei einer ungeraden Anzahl von Ziffern liegt die Symmetrieachse genau auf der mittleren Ziffer, bei einer geraden Anzahl von Stellen dagegen zwischen den beiden mittleren Ziffern.
-Palindroms. Diese Stellenanzahl ist von Bedeutung, weil sie den Charakter der Symmetrieeigenschaft des Palindroms unmittelbar beeinflusst. Bei einer ungeraden Anzahl von Ziffern liegt die Symmetrieachse genau auf der mittleren Ziffer, bei einer geraden Anzahl von Stellen dagegen zwischen den beiden mittleren Ziffern.
Grundsätzlich lässt sich die Anzahl der Ziffern des ![]() -ten Basis-
-ten Basis-![]() -Palindroms aus der Anzahl der Stellen von
-Palindroms aus der Anzahl der Stellen von ![]() – geschrieben als Basis-
– geschrieben als Basis-![]() -Zahl – und dem betreffenden Wertebereich bestimmen.
-Zahl – und dem betreffenden Wertebereich bestimmen.
Die nachfolgend für ![]() definierten Hilfsfunktionen
definierten Hilfsfunktionen ![]() und
und ![]() erlauben direkt die Bestimmung der gesuchten Stellenanzahl
erlauben direkt die Bestimmung der gesuchten Stellenanzahl ![]() . Mit
. Mit
(99) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \lambda_{b}(n) &:= \left\lfloor \log_{b}\left(\max\left(1,\frac{b}{b+1}\cdot n \right) \right) \right\rfloor \\[8pt] \overline{\lambda_{b}}(n) &:= \left\lfloor \log_{b}\left(\max\left(1,\frac{1}{2} \cdot n\right) \right) \right\rfloor \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-cc9ee68acb39a21a56195c6aefb57310_l3.png)
ergibt sich
(100) ![Rendered by QuickLaTeX.com \begin{equation*} L\left(P_{b}(n)\right) = \begin{cases} 2 \cdot \lambda_{b}(n) +1, &\text{wenn} \; \lambda_{b}(n) = \overline{\lambda_{b}}(n) \\[8pt] 2 \cdot \lambda_{b}(n), &\text{sonst} \end{cases} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-e024649d0c6a272760819baec5624ca2_l3.png)
Da ![]() entweder gleich
entweder gleich ![]() oder um
oder um ![]() kleiner ist, wird die Stellenanzahl von
kleiner ist, wird die Stellenanzahl von ![]() im Falle der Ungleichheit
im Falle der Ungleichheit ![]() durch die Summe
durch die Summe ![]() bestimmt. Man kann daher für die Stellenanzahl von
bestimmt. Man kann daher für die Stellenanzahl von ![]() auch schreiben
auch schreiben
(101) ![]()
Nach dem Vorstehenden ist somit die Stellenanzahl ungerade im ersteren Falle, wenn also ![]() , andernfalls, wenn also
, andernfalls, wenn also ![]() , ist sie gerade. Demnach gilt auch
, ist sie gerade. Demnach gilt auch
(102) ![]()
sowie
(103) ![]()
7.1 Rekursive Berechnung
Die folgende Beziehung erlaubt für ![]() die rekursive Berechnung des
die rekursive Berechnung des ![]() -ten Basis-
-ten Basis-![]() -Palindroms.
-Palindroms.
(104) ![]()
Dabei sind die Parameter ![]() und
und ![]() folgendermaßen zu bestimmen:
folgendermaßen zu bestimmen:
(105) ![Rendered by QuickLaTeX.com \begin{align*} q &= \lambda_{b}(n) + \overline{\lambda_{b}}(n) \\[8pt]d &= \displaystyle \left(\left\lfloor \frac{n}{b^{ \left\lfloor\frac{q}{2}\right\rfloor}} \right\rfloor -1 + q \bmod 2 \right) \bmod b \end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-1075a4eee1ebba2cbde0527439e4d3bc_l3.png)
Wegen ![]() kann man dabei auch direkt auf die
kann man dabei auch direkt auf die ![]() -Funktionen zurückgreifen. Die weiteren Parameter
-Funktionen zurückgreifen. Die weiteren Parameter ![]() und
und ![]() bestimmt man mittels des nachfolgend definierten Hilfsparameters
bestimmt man mittels des nachfolgend definierten Hilfsparameters ![]() .
.
(106) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} N &= \displaystyle \left(d+1+ (b-1)\cdot \left(q \bmod 2 \right) \right) \cdot b^{ \left\lfloor\frac{q}{2}\right\rfloor} \\[8pt] m &= \begin{cases} 1, &\text{wenn} \; n = N \\[4pt] n - N + b^{\displaystyle \left\lfloor\log_{b}\left(n-N\right) \right\rfloor + q \bmod 2}, &\text{sonst} \end{cases} \\[8pt]p &= \lambda_{b}(n) - \lambda_{b}(m) \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-39a76e9e94f25e75b44294c83fa0fedd_l3.png)
Die Stellenanzahl ![]() des Palindroms ist
des Palindroms ist ![]() . Demnach hat das gesuchte Palindrom eine ungerade Anzahl von Stellen, wenn
. Demnach hat das gesuchte Palindrom eine ungerade Anzahl von Stellen, wenn ![]() gerade ist, und eine gerade Anzahl von Stellen, wenn
gerade ist, und eine gerade Anzahl von Stellen, wenn ![]() ungerade ist.
ungerade ist.
Nehmen wir als Beispiel Palindrome zur Basis ![]() sowie
sowie ![]() für
für ![]() . Die ersten
. Die ersten ![]() dieser Palindrome sind:
dieser Palindrome sind:
(107) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array} {lll} P_{5}(n), &1 \le n \le 20: \;\\ &0,1,2,3,4,11,22,33,44,101,111, 121, \\&131, 141, 202, 212, 222, 232, 242, 303, \cdots &\text{(Basis 5)} \\&0,1,2,3,4,6,12,18,24,26,31,36,\\&41,46,52,57,62,67,72,78, \cdots &\text{(dezimal)} \\[8pt]P_{7}(n), &1 \le n \le 20: \;\\ &0,1,2,3,4,5,6,11,22,33,44,55,\\&66,101,111,121,131,141,151,161, \cdots &\text{(Basis 7)} \\&0,1,2,3,4,5,6,8,16,24,32,40,\\&48,50,57,64,71,78,85,92, \cdots &\text{(dezimal)} \end{array} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-86f21d6311ef204a0c6688c3f46bf5c2_l3.png)
Nun bestimmen wir ![]() rekursiv und erhalten
rekursiv und erhalten
(108) 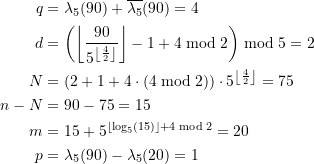
Mit ![]() bekommen wir
bekommen wir
(109) 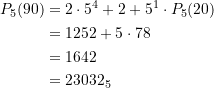
Völlig analog verläuft die rekursive Berechnung von ![]()
(110) 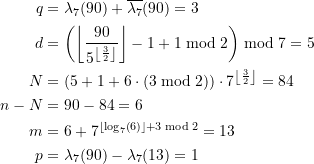
Unter Berücksichtigung von ![]() erhalten wir
erhalten wir
(111) 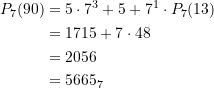
7.2 Direkte Berechnung
Das ![]() -te Palindrom in Basis-
-te Palindrom in Basis-![]() kann für
kann für ![]() auf dem nachfolgend beschriebenen Wege direkt berechnet werden.
auf dem nachfolgend beschriebenen Wege direkt berechnet werden.
Wir setzen ![]() und unterscheiden zwei Fälle.
und unterscheiden zwei Fälle.
Fall 1: ![]()
(112) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{b}(n) &=\sum \limits_{k=1}^{m-1} \left(\left\lfloor \frac{n}{b^{m-k}}\right\rfloor \bmod b\right)\left(b^k + b^{2m-k}\right) \; + \\[4pt]& \quad \, \left( \left\lfloor \frac{n}{b^m} \right\rfloor -1 \right) \left(1 + b^{2m}\right) + \left(n \bmod b \right) \cdot b^m \\[10pt]&= \sum \limits_{k=1}^{m-1} \left(\left\lfloor \frac{n}{b^{m-k}}\right\rfloor \bmod b\right) \cdot b^k \;+ \\[4pt] & \quad \, \left(n - b^m\right) \cdot b^m + \left\lfloor \frac{n}{b^m} \right\rfloor -1 \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-8e0896c324a3c0f5b6eec351d9076a00_l3.png)
Fall 2: ![]()
(113) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P_{b}(n) &=\sum \limits_{k=0}^{m-1} \left(\left\lfloor \frac{n}{b^{m-k-1}}\right\rfloor \bmod b\right)\left(b^{k} + b^{2m-k-1}\right) \\[8pt]&= \sum \limits_{k=1}^{m-1} \left(\left\lfloor \frac{n}{b^{m-k}}\right\rfloor \bmod b\right)\cdot b^{k-1} \;+ \\[4pt] & \quad \, \left(n - b^m\right) \cdot b^m + \left( n \bmod b\right) \cdot b^{m-1} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-d511326cc06abcf28e13b4db93f77b1c_l3.png)
Betrachten wir auch betreffend der direkten Berechnung zwei Beispiele und nehmen dafür Palindrome zur Basis ![]() sowie
sowie ![]() für
für ![]() . Die ersten
. Die ersten ![]() dieser Palindrome sind:
dieser Palindrome sind:
(114) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array} {lll} P_{6}(n), \; &1 \le n \le 20: \\ &0,1,2,3,4,5,11,22,33,44,55,101,\\ &111, 121, 131, 141, 151, 202, 212, 222, \cdots &\text{(Basis 6)} \\&0,1,2,3,4,5,7,14,21,28,35,37,\\ &43,49,55,61,67,74,80,86, \cdots &\text{(dezimal)} \\[8pt]P_{9}(n), \; &1 \le n \le 20: \;\\ &0,1,2,3,4,5,6,7,8,11,22,33,\\&44,55,66,77,88,101,111,121, \cdots &\text{(Basis 9)} \\&0,1,2,3,4,5,6,7,8,10,20,30,\\ &40,50,60,70,80,82,91,100, \cdots &\text{(dezimal)} \end{array} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-9f622e1d047dc37b1b408240f7521951_l3.png)
Zunächst das Beispiel ![]() . Es gilt
. Es gilt ![]() , demnach liegt der Fall 2 mit
, demnach liegt der Fall 2 mit ![]() vor. Die beiden Terme des Summenausdrucks sind
vor. Die beiden Terme des Summenausdrucks sind ![]() und
und ![]() . Die äußeren Summanden ergeben
. Die äußeren Summanden ergeben ![]() und
und ![]() . Zusammen folgt
. Zusammen folgt ![]() .
.
Für das Beispiel ![]() erhalten wir,
erhalten wir, ![]() , demnach liegt der Fall 1 mit
, demnach liegt der Fall 1 mit ![]() vor. Der einzige Term des Summenausdrucks ist
vor. Der einzige Term des Summenausdrucks ist ![]() . Die äußeren Summanden ergeben
. Die äußeren Summanden ergeben ![]() und
und ![]() . Zusammen bekommen wir die Summe
. Zusammen bekommen wir die Summe ![]() .
.
7.3 Anschauliche Bestimmung
Die anschauliche Bestimmung des ![]() -ten Basis-
-ten Basis-![]() -Palindroms verläuft ähnlich, wie im Fall der dezimalen Palindrome. Zunächst muss
-Palindroms verläuft ähnlich, wie im Fall der dezimalen Palindrome. Zunächst muss ![]() im Basis-
im Basis-![]() -Ziffernsystem dargestellt werden. Mit
-Ziffernsystem dargestellt werden. Mit ![]() erhält man:
erhält man:
(115) ![Rendered by QuickLaTeX.com \begin{equation*} P_{b}(n) \Leftrightarrow \begin{cases} \large \left[ \, d_1-1\; d_2\; d_3 \cdots d_k \cdots d_3\; d_2\; d_1 -1 \,\right]_b, & \text{falls}\; d_1 > 1 \\[4pt]\large \left[ \, b-1\; d_3 \cdots d_k \cdots d_3\; b-1 \, \right]_b, & \text{falls}\; d_1 = 1 \; \text{und} \; d_2 = 0 \\[4pt]\large \left[ \, d_2\; d_3 \cdots d_k\; d_k \cdots d_3\; d_2 \,\right]_b, & \text{falls}\; d_1 = 1 \; \text{und} \; d_2 > 0 \end{cases} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-8d44b492957eeb86fd5ad7a9a73e62a0_l3.png)
Beispiel: ![]() . Wir haben
. Wir haben ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() . Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Demzufolge bekommen wir die Ziffernfolge von
. Nach der Fallunterscheidung trifft der erstgenannte Fall zu. Demzufolge bekommen wir die Ziffernfolge von ![]() zu
zu ![]() , also
, also ![]() .
.
7.4 Umkehrungsformel
Die Frage nach dem betreffenden Indexwert ![]() , für den gilt
, für den gilt ![]() für ein vorgegebenes Basis-
für ein vorgegebenes Basis-![]() -Palindrom
-Palindrom ![]() , ist in Analogie zu den dezimalen Palindromen ebenfalls einfach zu beantworten. Mir der Definition
, ist in Analogie zu den dezimalen Palindromen ebenfalls einfach zu beantworten. Mir der Definition ![]() gilt:
gilt:
(116) ![]()
Nehmen wir ![]() als Beispielpalindrom für Basis
als Beispielpalindrom für Basis ![]() . Wir finden
. Wir finden ![]() .
.
Ein weiteres Beispiel mit Basis ![]() ist
ist ![]() . Hierfür ergibt sich
. Hierfür ergibt sich ![]() . Für Basis
. Für Basis ![]() folgt bei der formal gleichen Ziffernfolge
folgt bei der formal gleichen Ziffernfolge ![]() das Ergebnis
das Ergebnis ![]()
7.5 Anzahlfunktion
Für Potenzen zur Basis-![]() folgt direkt die Anzahl der Basis-
folgt direkt die Anzahl der Basis-![]() -Palindrome zwischen
-Palindrome zwischen ![]() und
und ![]() zu
zu
(117) ![]()
Für die Anzahl der Basis-![]() -Palindrome
-Palindrome ![]() ,
, ![]() , ergibt sich daher nach Aufaddieren vorgenannter Partialsummen
, ergibt sich daher nach Aufaddieren vorgenannter Partialsummen
(118) ![Rendered by QuickLaTeX.com \begin{align*} A_{b}\left(b^{n}\right) &= \displaystyle \begin{cases} 2\cdot b^{\frac{n}{2}} - 1, \; &n \bmod 2 = 0 \\[4pt]\displaystyle (b+1)\cdot b^{\frac{n-1}{2}} - 1, \; &n \bmod 2 = 1 \end{cases} \\[8pt]&= \displaystyle \left(2 + (b-1)\cdot n \bmod 2\right) \cdot b^{\left\lfloor\frac{n}{2}\right\rfloor} - 1 \\[8pt] &= \displaystyle \frac{b+3 - (b-1)\cdot (-1)^n}{2} \cdot b^{\left\lfloor\frac{n}{2}\right\rfloor} - 1\end{align*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-b92a5e74a2253b0ac0edec828854903f_l3.png)
7.6 Wachstum der Folge von Palindromen zur Basis b
Palindrome zur Basis ![]() gehorchen für
gehorchen für ![]() der Ungleichung
der Ungleichung
(119) ![]()
Beim Grenzübergang ![]() gilt
gilt
(120) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \liminf_{n \rightarrow \infty} \frac{P_b(n)}{n^2} &= \frac{b}{(b+1)^2} \\[4pt] \limsup_{n \rightarrow \infty} \frac{P_b(n)}{n^2} &= \frac{1}{4} \end{split} \end{equation*}](https://web.sumymus.de/wp-content/ql-cache/quicklatex.com-e2e9b151c3b682d98d66abbcb62a9b91_l3.png)
7.7 Rechenoperationen mit Palindromen
Generell bezeichnen wir die Ziffernfolge einer Basis-![]() -Zahl
-Zahl ![]() symbolisch mit
symbolisch mit ![]() bzw.
bzw. ![]() . Die numerische Zahl
. Die numerische Zahl ![]() entspricht demnach der Ziffernfolge
entspricht demnach der Ziffernfolge ![]() . Zu einer Ziffer
. Zu einer Ziffer ![]() ,
, ![]() , steht
, steht ![]() für die Ziffernfolge von
für die Ziffernfolge von ![]() gleichen Ziffern, also etwa
gleichen Ziffern, also etwa ![]() , entsprechend dem numerischen Wert
, entsprechend dem numerischen Wert ![]() . Wenn die Basis nicht direkt mit notiert ist, dann ergibt sich diese entweder aus dem Kontext, oder es ist die Basis
. Wenn die Basis nicht direkt mit notiert ist, dann ergibt sich diese entweder aus dem Kontext, oder es ist die Basis ![]() gemeint. Im Ziffernsystem
gemeint. Im Ziffernsystem ![]() notieren wir im vorigen Beispiel
notieren wir im vorigen Beispiel ![]() .
.
Die Anzahl der Ziffern von ![]() bzw. von
bzw. von ![]() bezeichnen wir symbolisch mit
bezeichnen wir symbolisch mit ![]() .
.
Die Ziffernfolge von ![]() ohne die erste Ziffer, also nur die Ziffern rechts nach der ersten Ziffer notieren wir als
ohne die erste Ziffer, also nur die Ziffern rechts nach der ersten Ziffer notieren wir als ![]() . Analog bedeutet
. Analog bedeutet ![]() die Ziffernfolge von
die Ziffernfolge von ![]() ohne die letzte Ziffer, also nur die Ziffern links vor der letzten Ziffer. Für
ohne die letzte Ziffer, also nur die Ziffern links vor der letzten Ziffer. Für ![]() gilt also
gilt also ![]() und
und ![]() . Dagegen steht
. Dagegen steht ![]() für die
für die ![]() -te Ziffer in der Ziffernfolge
-te Ziffer in der Ziffernfolge ![]() , wobei
, wobei ![]() . Wenn die Basis angegeben wird, so gilt
. Wenn die Basis angegeben wird, so gilt ![]() .
.
Liegen zwei Basis-![]() -Zahlen
-Zahlen ![]() und
und ![]() vor, so bedeutet
vor, so bedeutet ![]() die Verkettung (Concatenation) der beiden Ziffernfolgen. Der Zahlenwert
die Verkettung (Concatenation) der beiden Ziffernfolgen. Der Zahlenwert ![]() der Verkettung entspricht numerisch der Summe
der Verkettung entspricht numerisch der Summe ![]() .
.
Die stellenweise Addition von ![]() und
und ![]() bezeichnen wir mit
bezeichnen wir mit ![]() , also
, also ![]() . Um die Addition nicht rechtsbündig sondern geeignet nach links verschoben durchzuführen, verkettet man
. Um die Addition nicht rechtsbündig sondern geeignet nach links verschoben durchzuführen, verkettet man ![]() oder
oder ![]() entsprechend mit einer Hilfsgröße. Z.B. ist
entsprechend mit einer Hilfsgröße. Z.B. ist ![]() . Man erkennt bereits hier, wie solchermaßen Palindrome konstruiert werden können. Analog verfahren wir bei der Subtraktion:
. Man erkennt bereits hier, wie solchermaßen Palindrome konstruiert werden können. Analog verfahren wir bei der Subtraktion: ![]() .
.
7.7.1 Konstruktion von Palindromen
Sei ![]() eine Basis-
eine Basis-![]() -Zahl,
-Zahl, ![]() sei die Zahl mit der in Bezug auf
sei die Zahl mit der in Bezug auf ![]() umgekehrten Ziffernreihenfolge.
umgekehrten Ziffernreihenfolge.
7.7.1-(1) ![]() ist ein Basis-
ist ein Basis-![]() -Palindrom. Numerisch bestimmt sich der Wert mittels
-Palindrom. Numerisch bestimmt sich der Wert mittels ![]() , wobei
, wobei ![]() . Die Stellenanzahl von
. Die Stellenanzahl von ![]() ist ungerade und es gilt
ist ungerade und es gilt ![]() . Die Verkettung
. Die Verkettung ![]() liefert identisch das Palindrom
liefert identisch das Palindrom ![]() . Die numerische Berechnung hierfür lautet
. Die numerische Berechnung hierfür lautet ![]() .
.
7.7.1-(2) ![]() ist ein Basis-
ist ein Basis-![]() -Palindrom. Numerisch gilt:
-Palindrom. Numerisch gilt: ![]() , wobei
, wobei ![]() . Die Stellenanzahl von
. Die Stellenanzahl von ![]() ist gerade und es gilt
ist gerade und es gilt ![]() .
.
7.7.1-(3) Wenn ![]() ein Basis-
ein Basis-![]() -Palindrom ist, dann ist auch
-Palindrom ist, dann ist auch ![]() ein Palindrom. Numerisch gilt:
ein Palindrom. Numerisch gilt: ![]() , wobei
, wobei ![]() . Die Stellenanzahl von
. Die Stellenanzahl von ![]() ist
ist ![]() .
.
Natürlich ist für jede Ziffer ![]() bereits jede Verkettung
bereits jede Verkettung ![]() ,
, ![]() , ein Palindrom, weil auch
, ein Palindrom, weil auch ![]() ein Palindrom ist.
ein Palindrom ist.
Beispiel 1: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Es folgt
. Es folgt ![]() . Numerisch erhalten wir
. Numerisch erhalten wir ![]() . Ebenso:
. Ebenso: ![]() , jeweils mit der Stellenanzahl
, jeweils mit der Stellenanzahl ![]()
Beispiel 2: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Nun ergibt sich
. Nun ergibt sich ![]() sowie
sowie ![]() . Die Stellenanzahl ist
. Die Stellenanzahl ist ![]() .
.
Beispiel 3: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Zunächst ist
. Zunächst ist ![]() . Numerisch erhalten wir:
. Numerisch erhalten wir: ![]() , und somit
, und somit ![]() .
.
7.7.2 Summen von Palindromen
7.7.2-(1) Definition. Zwei Basis-![]() -Palindrome
-Palindrome ![]() und
und ![]() heißen summenkompatibel oder kurz S-kompatibel, wenn
heißen summenkompatibel oder kurz S-kompatibel, wenn
(i) ![]() und
und
(ii) ![]() und
und
(iii) Für alle ![]() gilt
gilt ![]() , wobei
, wobei ![]() .
.
7.7.2-(2) Summe. Seien ![]() und
und ![]() zwei S-kompatible Basis-
zwei S-kompatible Basis-![]() -Palindrome. Dann ist mit
-Palindrome. Dann ist mit ![]() auch die Summe
auch die Summe ![]() ein Basis-
ein Basis-![]() -Palindrom.
-Palindrom.
Beispiel 1: ![]() ,
, ![]() ,
, ![]() . (i) und (ii) sind erfüllt und wir haben
. (i) und (ii) sind erfüllt und wir haben ![]() . Für
. Für ![]() gilt
gilt ![]() , womit die Werte sämtlich
, womit die Werte sämtlich ![]() sind. Folglich erhalten wir
sind. Folglich erhalten wir ![]() als das Summenpalindrom.
als das Summenpalindrom.
Wenn in der Situation von 7.7.2-(2) die Stellenanzahl der beiden Palindrome ![]() und
und ![]() gleich ist, dann ist bereits die einfache Summe
gleich ist, dann ist bereits die einfache Summe ![]() ein Palindrom.
ein Palindrom.
7.7.2-(3) Seien ![]() und
und ![]() die beiden Nummern, so dass
die beiden Nummern, so dass ![]() und
und ![]() .
.
Mit ![]() gilt sodann
gilt sodann ![]() ,
,
wobei ![]()
Beispiel 2: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Wir haben
. Wir haben ![]() und
und ![]() sowie
sowie ![]() und es gilt
und es gilt ![]() .
.
7.7.2-(4) Summe Modulo b. Seien ![]() und
und ![]() zwei Basis-
zwei Basis-![]() -Palindrome. Dann ist unter der Voraussetzung 7.7.2-(1) (i) und (ii) auch die ziffernweise Modulo-
-Palindrome. Dann ist unter der Voraussetzung 7.7.2-(1) (i) und (ii) auch die ziffernweise Modulo-![]() -Summe
-Summe ![]() ein Basis-
ein Basis-![]() -Palindrom.
-Palindrom.
Beispiel 3: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() , da bei der ziffernweisen Addition
, da bei der ziffernweisen Addition ![]() ist.
ist.
7.7.3 Differenzen von Palindromen
7.7.3-(1) Zwei Basis-![]() -Palindrome
-Palindrome ![]() und
und ![]() heißen differenzkompatibel oder kurz D-kompatibel, wenn
heißen differenzkompatibel oder kurz D-kompatibel, wenn
(i) ![]() und
und
(ii) ![]() und
und
(iii) Für alle ![]() gilt
gilt ![]() , wobei
, wobei ![]() .
.
7.7.3-(2) Differenz. Seien ![]() und
und ![]() zwei D-kompatible Basis-
zwei D-kompatible Basis-![]() -Palindrome. Dann ist mit
-Palindrome. Dann ist mit ![]() auch die Differenz
auch die Differenz ![]() ein Basis-
ein Basis-![]() -Palindrom.
-Palindrom.
Beispiel 1: ![]() ,
, ![]() ,
, ![]() . (i) und (ii) sind erfüllt und wir haben
. (i) und (ii) sind erfüllt und wir haben ![]() . Für
. Für ![]() gilt
gilt ![]() , womit die Werte sämtlich
, womit die Werte sämtlich ![]() sind. Folglich erhalten wir
sind. Folglich erhalten wir ![]() als das Differenzpalindrom.
als das Differenzpalindrom.
Wenn in der Situation von 7.7.3-(2) die Stellenanzahl der beiden Palindrome ![]() und
und ![]() gleich ist, dann ist bereits die einfache Differenz
gleich ist, dann ist bereits die einfache Differenz ![]() ein Palindrom.
ein Palindrom.
7.7.3-(3) Seien ![]() und
und ![]() die beiden Nummern, so dass
die beiden Nummern, so dass ![]() und
und ![]() .
.
Mit ![]() gilt sodann
gilt sodann ![]() ,
,
wobei ![]() .
.
Beispiel 2: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Wir haben
. Wir haben ![]() und
und ![]() sowie
sowie ![]() und es gilt
und es gilt ![]() .
.
7.7.3-(4) Differenz Modulo b. Seien ![]() und
und ![]() zwei Basis-
zwei Basis-![]() -Palindrome. Dann ist unter der Voraussetzung 7.7.3-(1) (i) und (ii) auch die ziffernweise Modulo-
-Palindrome. Dann ist unter der Voraussetzung 7.7.3-(1) (i) und (ii) auch die ziffernweise Modulo-![]() -Differenz
-Differenz ![]() ein Basis-
ein Basis-![]() -Palindrom.
-Palindrom.
Beispiel 3: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() , da bei der ziffernweisen Subtraktion
, da bei der ziffernweisen Subtraktion ![]() gilt.
gilt.
7.8 Existenz
7.8.1 Definitionen und einfache Folgerungen
7.8.1-(1) Definition. Jede Zahl ![]() ist ein Palindrom in allen Basen
ist ein Palindrom in allen Basen ![]() . Solche Palindrome nennen wir trivial, da sie nur aus einer Ziffer bestehen.
. Solche Palindrome nennen wir trivial, da sie nur aus einer Ziffer bestehen.
7.8.1.-(2) Definition. Ein Basis-![]() -Palindrom
-Palindrom ![]() heißt nicht-trivial, wenn
heißt nicht-trivial, wenn ![]() . Ein solches Palindrom hat mindestens 2 Ziffern.
. Ein solches Palindrom hat mindestens 2 Ziffern.
7.8.1-(3) Definition. Ein Basis-![]() -Palindrom
-Palindrom ![]() heißt schwach, wenn gilt
heißt schwach, wenn gilt ![]() . Ein solches Palindrom hat genau 2 Ziffern.
. Ein solches Palindrom hat genau 2 Ziffern.
7.8.1-(4) Definition. Ein Basis-![]() -Palindrom
-Palindrom ![]() heißt stark oder echt, wenn gilt
heißt stark oder echt, wenn gilt ![]() . Ein solches Palindrom hat mindestens 3 Ziffern.
. Ein solches Palindrom hat mindestens 3 Ziffern.
Folgerungen:
![]() sind triviale Palindrome in allen Basen
sind triviale Palindrome in allen Basen ![]() .
.![]() ist ein triviales Palindrom in allen Basen
ist ein triviales Palindrom in allen Basen ![]() .
.
Jede Zahl ![]() ist ein schwaches Palindrom in Basis
ist ein schwaches Palindrom in Basis ![]() , denn es gilt
, denn es gilt ![]() .
.
![]() ist ein schwaches Palindrom in Basis
ist ein schwaches Palindrom in Basis ![]() , wegen
, wegen ![]() .
.![]() ist ein schwaches Palindrom in Basis
ist ein schwaches Palindrom in Basis ![]() , wegen
, wegen ![]() .
.
![]() ist ein starkes Palindrom in Basis
ist ein starkes Palindrom in Basis ![]() , wegen
, wegen ![]() .
. ![]() ist das kleinste starke Palindrom.
ist das kleinste starke Palindrom.
![]() ist ein schwaches Palindrom in Basis
ist ein schwaches Palindrom in Basis ![]() , wegen
, wegen ![]() .
.![]() ist ein starkes Palindrom in Basis
ist ein starkes Palindrom in Basis ![]() , wegen
, wegen ![]() .
.![]() ist ein schwaches Palindrom in Basis
ist ein schwaches Palindrom in Basis ![]() , wegen
, wegen ![]() , und gleichfalls ein schwaches Palindrom in Basis
, und gleichfalls ein schwaches Palindrom in Basis ![]() , wegen
, wegen ![]() ,
,
7.8.2 Existenzsätze – hinreichende Bedingungen
7.8.2-(1) Jede gerade Zahl ![]() ist ein nicht-triviales Palindrom in Basis
ist ein nicht-triviales Palindrom in Basis ![]() .
.
Beweis: Es gilt ![]() und
und ![]() .
. ![]()
7.8.2-(2) Jede durch ![]() teilbare Zahl
teilbare Zahl ![]() ist ein nicht-triviales Palindrom in Basis
ist ein nicht-triviales Palindrom in Basis ![]() .
.
Beweis: Es gilt ![]() und
und ![]() .
. ![]()
7.8.2-(3) Jede durch ![]() teilbare Zahl
teilbare Zahl ![]() ist ein nicht-triviales Palindrom in Basis
ist ein nicht-triviales Palindrom in Basis ![]() .
.
Beweis: Es gilt ![]() und
und ![]() .
. ![]()
7.8.2-(4) Zu jeder zusammengesetzten Zahl ![]() gibt es eine Basis
gibt es eine Basis ![]() , so dass
, so dass ![]() ein schwaches oder ein echtes Palindrom in Basis
ein schwaches oder ein echtes Palindrom in Basis ![]() ist.
ist.
Beweis: Nach Wahl von ![]() gibt es nicht-triviale Teiler
gibt es nicht-triviale Teiler ![]() und
und ![]() , so dass
, so dass ![]() . OBdA sei
. OBdA sei ![]() . Nach Voraussetzung gilt
. Nach Voraussetzung gilt ![]() , und
, und ![]() . Wenn
. Wenn ![]() , dann
, dann ![]() , wenn
, wenn ![]() , dann
, dann ![]() .
.
Wir treffen die folgende Fallunterscheidung:
(A) ![]() .
.
Mit ![]() ergibt sich
ergibt sich ![]() , wobei
, wobei ![]() und
und ![]() . Demnach ist
. Demnach ist ![]() ein schwaches Palindrom.
ein schwaches Palindrom.
(B) ![]() .
.
Dann ist ![]() und
und ![]() gerade. Wir setzen
gerade. Wir setzen ![]() . Es ergibt sich
. Es ergibt sich ![]() mit
mit ![]() und
und ![]() . Daher ist
. Daher ist ![]() ein schwaches Palindrom.
ein schwaches Palindrom.
(C) ![]() .
. ![]() ist eine Quadratzahl
ist eine Quadratzahl ![]() , also
, also ![]() mit
mit ![]() . Für
. Für ![]() haben wir mit
haben wir mit ![]() ,
, ![]() , also
, also ![]() .
. ![]() ist ein echtes Palindrom mit
ist ein echtes Palindrom mit ![]() . Für
. Für ![]() , also
, also ![]() , setzen wir
, setzen wir ![]() und bekommen
und bekommen ![]() , also
, also ![]() mit
mit ![]() . Demzufolge ist
. Demzufolge ist ![]() ist ein echtes Palindrom mit
ist ein echtes Palindrom mit ![]() .
. ![]()
Folgerung:
Alle Nicht-Primzahlen ![]() sind schwache oder echte Palindrome mit einer Basis
sind schwache oder echte Palindrome mit einer Basis ![]() .
.
7.8.2-(5) Jede Potenzzahl ![]() ,
, ![]() ,
, ![]() , ist ein schwaches Palindrom in Basis
, ist ein schwaches Palindrom in Basis ![]() .
.
Beweis: Wir unterscheiden die beiden Fälle ![]() und
und ![]() .
.
(A) ![]() .
.
Wir haben ![]() und setzen
und setzen ![]() . Damit erhalten wir
. Damit erhalten wir ![]() , wobei
, wobei ![]() . Somit gilt
. Somit gilt ![]() , und folglich
, und folglich ![]() .
.
(B) ![]() .
.
Hier setzen wir ![]() und
und ![]() . Damit bekommen wir
. Damit bekommen wir ![]() , wobei
, wobei ![]() . Somit gilt
. Somit gilt ![]() , und folglich
, und folglich ![]() .
. ![]()
7.8.2-(6) Jede Quadratzahl ![]() ,
, ![]() , ist ein echtes Palindrom in Basis
, ist ein echtes Palindrom in Basis ![]() mit
mit ![]() Ziffern.
Ziffern.
Beweis: ![]() , mithin
, mithin ![]() , also
, also ![]() mit
mit ![]() .
. ![]()
7.8.2-(7) Jede Kubikzahl ![]() ,
, ![]() , ist ein echtes Palindrom in Basis
, ist ein echtes Palindrom in Basis ![]() mit
mit ![]() Ziffern.
Ziffern.
Beweis: ![]() , daher
, daher ![]() , also
, also ![]() mit
mit ![]() .
. ![]()
Die vorgenannte Feststellung gilt ganz allgemein für alle Potenzzahlen.
7.8.2-(8) Jede Potenzzahl ![]() ,
, ![]() gerade,
gerade, ![]() , ist ein echtes Palindrom in Basis
, ist ein echtes Palindrom in Basis ![]() mit
mit ![]() Ziffern.
Ziffern.
Beweis: ![]() , also
, also ![]() .
.
Der größte Term ![]() in der Summe ist der Wert für
in der Summe ist der Wert für ![]() und beläuft sich auf
und beläuft sich auf ![]() . Dieser Wert ist nach Voraussetzung
. Dieser Wert ist nach Voraussetzung ![]() .
. ![]()
Demnach erhalten wir die Darstellung im Basis-![]() -Ziffernsystem zu
-Ziffernsystem zu ![]() . Aufgrund der Symmetrie der Binomialfaktoren, also
. Aufgrund der Symmetrie der Binomialfaktoren, also ![]() , für
, für ![]() , ist folglich
, ist folglich ![]() ein Palindrom in Basis
ein Palindrom in Basis ![]() .
. ![]()
7.8.2-(9) Jede Potenzzahl ![]() ,
, ![]() ungerade,
ungerade, ![]() , ist ein echtes Palindrom in Basis
, ist ein echtes Palindrom in Basis ![]() mit
mit ![]() Ziffern. Die beiden zentralen Ziffern des Palindroms sind gleich.
Ziffern. Die beiden zentralen Ziffern des Palindroms sind gleich.
Beweis: ![]() , also
, also ![]() .
.
Der größte Term ![]() in der Summe ist der Wert für
in der Summe ist der Wert für ![]() und beläuft sich auf
und beläuft sich auf ![]() . Dieser Wert ist nach Voraussetzung
. Dieser Wert ist nach Voraussetzung ![]() .
.
Demnach erhalten wir die Darstellung im Basis-![]() -Ziffernsystem zu
-Ziffernsystem zu ![]() . Aufgrund der Symmetrie der Binomialfaktoren, also
. Aufgrund der Symmetrie der Binomialfaktoren, also ![]() , für
, für ![]() , ist folglich
, ist folglich ![]() ein Palindrom in Basis
ein Palindrom in Basis ![]() . Dabei sind die beiden mittleren Ziffern für
. Dabei sind die beiden mittleren Ziffern für ![]() und
und ![]() gleich.
gleich. ![]()
Anmerkung: Die vorstehend definierten Potenzzahl-Palindrome nennen wir Pascal’sche Palindrome, da sich die Ziffern ihrer Basis-![]() -Darstellung in offensichtlicher Weise in Analogie zum Pascal’schen Dreieck ableiten lassen.
-Darstellung in offensichtlicher Weise in Analogie zum Pascal’schen Dreieck ableiten lassen.
Beispiel: k = 4. Nach Voraussetzung muss ![]() sein.
sein.
Sei ![]() , somit
, somit ![]() . Wir erhalten
. Wir erhalten ![]() , und weiter
, und weiter ![]() , mithin
, mithin ![]() .
.
Sei ![]() , somit
, somit ![]() . Nun ist
. Nun ist ![]() , sowie
, sowie ![]() , mithin
, mithin ![]() .
.
k = 5. Nach Voraussetzung muss ![]() sein.
sein.
Sei ![]() , somit
, somit ![]() . Wir erhalten
. Wir erhalten ![]() und folglich
und folglich ![]() , somit
, somit ![]() . Dabei haben wir anstelle von
. Dabei haben wir anstelle von ![]() die „Ziffer“
die „Ziffer“ ![]() gesetzt.
gesetzt.
Sei ![]() , somit
, somit ![]() . Wir erhalten
. Wir erhalten ![]() und folglich
und folglich ![]() , also
, also ![]() . Auch hier haben wir die Ersetzung
. Auch hier haben wir die Ersetzung ![]() zugrunde gelegt,, wie im Hexadezimalsystem üblich.
zugrunde gelegt,, wie im Hexadezimalsystem üblich.
7.8.2-(10) Jede Potenzzahl ![]() ,
, ![]() ,
, ![]() , ist ein echtes Palindrom in Basis
, ist ein echtes Palindrom in Basis ![]() mit
mit ![]() Ziffern.
Ziffern.
Beweis: ![]() , mithin
, mithin ![]() , also
, also ![]() mit
mit ![]() .
. ![]()
7.8.2-(11) Jede Potenzzahl ![]() ,
, ![]() ,
, ![]() , ist ein echtes Palindrom in Basis
, ist ein echtes Palindrom in Basis ![]() mit
mit ![]() Ziffern.
Ziffern.
Beweis: ![]() , mithin
, mithin ![]() , also
, also ![]() mit
mit ![]() .
. ![]()
7.8.2-(12) Wenn für eine Zahl ![]() gilt,
gilt, ![]() ist eine Potenzzahl
ist eine Potenzzahl ![]() , also etwa
, also etwa ![]() , für ein
, für ein ![]() , und
, und ![]() , dann ist
, dann ist ![]() ein nicht-triviales Palindrom, und für
ein nicht-triviales Palindrom, und für ![]() ein echtes Palindrom in Basis
ein echtes Palindrom in Basis ![]() mit
mit ![]() Stellen.
Stellen.
Beweis: Es gilt ![]() mit
mit ![]() , und folglich
, und folglich ![]() .
. ![]()
Beispiel: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Wir haben
. Wir haben ![]() . und somit
. und somit ![]() .
.
7.8.2-(13) Wenn für eine Zahl ![]() gilt,
gilt, ![]() ist eine Potenzzahl
ist eine Potenzzahl ![]() , also etwa
, also etwa ![]() , für ein
, für ein ![]() , dann ist
, dann ist ![]() ein nicht-triviales Palindrom, und für
ein nicht-triviales Palindrom, und für ![]() (im Falle des Pluszeichens) bzw. für
(im Falle des Pluszeichens) bzw. für ![]() (im Falle des Minuszeichens) ein echtes Palindrom in Basis
(im Falle des Minuszeichens) ein echtes Palindrom in Basis ![]() mit
mit ![]() bzw. mit
bzw. mit ![]() Stellen.
Stellen.
Beweis: Es gilt ![]() . Mithin haben wir
. Mithin haben wir ![]() mit
mit ![]() Stellen im Falle des Pluszeichens sowie
Stellen im Falle des Pluszeichens sowie ![]() mit
mit ![]() Stellen im Falle des Minuszeichens.
Stellen im Falle des Minuszeichens. ![]()
Beispiele: ![]() ,
, ![]() ,
, ![]() . Wir haben
. Wir haben ![]() .
.![]() ,
, ![]() ,
, ![]() . Es gilt
. Es gilt ![]() .
.![]() ,
, ![]() ,
, ![]() . Hier folgt
. Hier folgt ![]() .
.
7.8.3 Existenzsätze – notwendige Bedingungen
Ein notwendiges Existenzkriterium kann folgendermaßen formuliert werden:
7.8.3-(1) Wenn ![]() ein Basis-
ein Basis-![]() -Palindrom ist, dann gilt mit
-Palindrom ist, dann gilt mit ![]()
![]() .
.
7.8.3-(2) Wenn mit ![]()
![]() oder
oder ![]() ,
,
dann ist ![]() kein Basis-
kein Basis-![]() -Palindrom mit
-Palindrom mit ![]() Stellen.
Stellen.
Beispiel: ![]() ,
, ![]() ,
, ![]() .
.
Es gilt ![]() , aber
, aber ![]() , also ist 100 kein Dezimalpalindrom mit 3 Stellen.
, also ist 100 kein Dezimalpalindrom mit 3 Stellen.![]() ,
, ![]() ,
, ![]() .
.![]() , also ist
, also ist ![]() ein Dezimalpalindrom. Demnach gilt
ein Dezimalpalindrom. Demnach gilt ![]() .
.
7.8.4 Exaktes Kriterium
7.8.4-(1) ![]() ist ein Palindrom vom Grade
ist ein Palindrom vom Grade ![]() genau dann, wenn es eine Basis
genau dann, wenn es eine Basis ![]() ,
,
(i) ![]() gibt, so dass mit
gibt, so dass mit
(ii) ![]() und
und
(iii) ![]()
![]() gilt.
gilt.
Beweis: Sei ![]() ein Palindrom vom Grade
ein Palindrom vom Grade ![]() . Dann gibt es
. Dann gibt es ![]() , so dass
, so dass ![]() .
.
Nun ist ![]() sowie
sowie ![]() , ferner
, ferner ![]() . Wenn wir hier
. Wenn wir hier ![]() einsetzen, dann erhalten wir
einsetzen, dann erhalten wir ![]() und somit
und somit ![]() . Nach 7.3 gilt daher
. Nach 7.3 gilt daher ![]() .
.
Im nächsten Schritt betrachten wir den Fall von Palindromen vom Grade ![]() . Dann gibt es
. Dann gibt es ![]() , so dass
, so dass ![]() .
.
Es ergibt sich ![]() sowie
sowie ![]() , ferner
, ferner ![]() . Wenn wir hier
. Wenn wir hier ![]() einsetzen, dann erhalten wir
einsetzen, dann erhalten wir ![]() und somit
und somit ![]() . Nach 7.3 gilt daher
. Nach 7.3 gilt daher ![]() .
. ![]()
7.8.4-(2) ![]() ist ein Palindrom vom Grade
ist ein Palindrom vom Grade ![]() genau dann, wenn
genau dann, wenn
(i) ![]() und eine Basis
und eine Basis ![]() ,
,
(ii) ![]() existiert, so dass mit
existiert, so dass mit
(iii) ![]() und
und
(iv) ![]()
![]() gilt.
gilt.
Beweis: Der Beweis läuft analog wir im Falle von 7.8.4-(1). Im Unterschied dazu müssen wir allerdings sukzessive alle Grade mit ![]() betrachten.
betrachten. ![]()
7.9 Floor und Ceiling
Es geht hier um die Bestimmung des nächstgrößeren und des nächstkleineren Basis-![]() -Palindroms zu einer gegebenen Zahl
-Palindroms zu einer gegebenen Zahl ![]() . Wir definieren
. Wir definieren
(i) ![]() und
und
(ii) ![]() .
.
7.9-(1) Wenn ![]() , dann ist
, dann ist ![]() ein Basis-
ein Basis-![]() -Palindrom.
-Palindrom.
7.9-(2) Wenn ![]() , dann ist
, dann ist ![]() das größte Basis-
das größte Basis-![]() -Palindrom
-Palindrom ![]() und
und ![]() das kleinste Basis-
das kleinste Basis-![]() -Palindrom
-Palindrom ![]() .
.
7.9-(3) Wenn ![]() , dann ist
, dann ist ![]() das kleinste Basis-
das kleinste Basis-![]() -Palindrom
-Palindrom ![]() und
und ![]() das größte Basis-
das größte Basis-![]() -Palindrom
-Palindrom ![]() .
.
Beispiele: ![]() hat im Dezimalsystem
hat im Dezimalsystem ![]() Ziffern. Wir erhalten folgerichtig
Ziffern. Wir erhalten folgerichtig ![]() und
und ![]() , also
, also ![]() .
.
Damit ergibt sich ![]() , also ist
, also ist ![]() kein Basis-
kein Basis-![]() -Palindrom. Ferner ist
-Palindrom. Ferner ist ![]() das größte Basis-
das größte Basis-![]() -Palindrom
-Palindrom ![]() und
und ![]() das kleinste Basis-
das kleinste Basis-![]() -Palindrom
-Palindrom ![]() .
.
![]() hat im Dezimalsystem
hat im Dezimalsystem ![]() Ziffern. Wir bekommen folgerichtig
Ziffern. Wir bekommen folgerichtig ![]() und
und ![]() , also
, also ![]() .
.
Daraus folgt ![]() , also ist
, also ist ![]() kein Basis-
kein Basis-![]() -Palindrom. Ferner ist
-Palindrom. Ferner ist ![]() das größte Basis-
das größte Basis-![]() -Palindrom
-Palindrom ![]() und
und ![]() das kleinste Basis-
das kleinste Basis-![]() -Palindrom
-Palindrom ![]() .
.
![]() hat im Dezimalsystem
hat im Dezimalsystem ![]() Ziffern. Wir erhalten
Ziffern. Wir erhalten ![]() und
und ![]() , also
, also ![]() .
.
Somit ![]() , also ist
, also ist ![]() kein Basis-
kein Basis-![]() -Palindrom. Ferner ist
-Palindrom. Ferner ist ![]() das kleinste Basis-
das kleinste Basis-![]() -Palindrom
-Palindrom ![]() und
und ![]() das größte Basis-
das größte Basis-![]() -Palindrom
-Palindrom ![]() .
.
7.10 Multiple Palindrome
Wir fragen: Wenn ![]() ein nicht-triviales Basis-
ein nicht-triviales Basis-![]() -Palindrom ist, gibt es dann eine Basis
-Palindrom ist, gibt es dann eine Basis ![]() , so dass
, so dass ![]() ein nicht-triviales Basis-
ein nicht-triviales Basis-![]() -Palindrom ist?
-Palindrom ist?
Im Allgemeinen ist das sicher nicht der Fall, z.B. ist ![]() ein nicht-triviales Basis-
ein nicht-triviales Basis-![]() -Palindrom, aber für alle Basen
-Palindrom, aber für alle Basen ![]() ist
ist ![]() kein Palindrom. Es gibt aber auch positive Beispiele. Dazu der nächste Satz:
kein Palindrom. Es gibt aber auch positive Beispiele. Dazu der nächste Satz:
7.10-(1) Wenn ![]() drei Teiler hat, die nicht alle gleich sind, dann gibt es mindestens zwei unterschiedliche Basen
drei Teiler hat, die nicht alle gleich sind, dann gibt es mindestens zwei unterschiedliche Basen ![]() und
und ![]() , so dass
, so dass ![]() ein
ein ![]() -Palindrom und zugleich ein
-Palindrom und zugleich ein ![]() -Palindrom ist.
-Palindrom ist.
Beweis: Sei ![]() mit
mit ![]() . Wenn
. Wenn ![]() , dann setzt man
, dann setzt man ![]() sowie
sowie ![]() und erhält
und erhält ![]() , also
, also ![]() sowie
sowie ![]() , also
, also ![]() .
.
Wenn ![]() , dann setzt man
, dann setzt man ![]() sowie
sowie ![]() und erhält
und erhält ![]() , also
, also ![]() sowie
sowie ![]() , also
, also ![]() .
. ![]()
Beispiel: ![]() ,
, ![]() ,
, ![]() . Wir haben folglich
. Wir haben folglich ![]() sowie
sowie ![]() .
.
Wir können noch eine allgemeinere Feststellung treffen:
7.10-(2) Nach Satz 7.8.2-(4) gibt es zu jeder zusammengesetzten Zahl ![]() eine Basis
eine Basis ![]() , so dass
, so dass ![]() ein nicht-triviales Basis-
ein nicht-triviales Basis-![]() -Palindrom ist. Auf der anderen Seite ist indessen jede Zahl
-Palindrom ist. Auf der anderen Seite ist indessen jede Zahl ![]() ein schwaches Palindrom zur Basis
ein schwaches Palindrom zur Basis ![]() .
.
Beweis: Wir müssen nur zeigen, dass für ![]() stets
stets ![]() gilt. Tatsächlich erhalten wir mit
gilt. Tatsächlich erhalten wir mit ![]() unmittelbar
unmittelbar ![]() , und damit weiter
, und damit weiter ![]() . Demnach erweist sich
. Demnach erweist sich ![]() für alle zusammengesetzten
für alle zusammengesetzten ![]() als palindromisch zu zwei unterschiedlichen Basen.
als palindromisch zu zwei unterschiedlichen Basen. ![]()
7.11 Minimale Basen
Wir haben gesehen, dass mit geeigneter Wahl der Basis b jede Zahl ein Palindrom ist. Zahlen <= 2 sind stets triviale Palindrome, alle anderen sind mindestens schwache Palindrome, also Palindrome vom Grade >= 2.
In der nachfolgenden Tabelle sind für die ersten 32 Zahlen die minimalen Basen und die resultierenden Palindromgrade aufgelistet.
| Minimale Basis | Grad des Palindroms | |
|---|---|---|
| 0 | 2 | 1 |
| 1 | 2 | 1 |
| 2 | 3 | 1 |
| 3 | 2 | 2 |
| 4 | 3 | 2 |
| 5 | 2 | 3 |
| 6 | 5 | 2 |
| 7 | 2 | 3 |
| 8 | 3 | 2 |
| 9 | 2 | 4 |
| 10 | 3 | 3 |
| 11 | 10 | 2 |
| 12 | 5 | 2 |
| 13 | 3 | 3 |
| 14 | 6 | 2 |
| 15 | 2 | 4 |
| 16 | 3 | 3 |
| 17 | 2 | 5 |
| 18 | 5 | 2 |
| 19 | 18 | 2 |
| 20 | 3 | 3 |
| 21 | 2 | 5 |
| 22 | 10 | 2 |
| 23 | 3 | 3 |
| 24 | 5 | 2 |
| 25 | 4 | 3 |
| 26 | 3 | 3 |
| 27 | 2 | 5 |
| 28 | 3 | 4 |
| 29 | 4 | 3 |
| 30 | 9 | 2 |
| 31 | 2 | 5 |
| 32 | 7 | 2 |
Nun fragen wir nach der kleinsten Basis ![]() , so dass ein vorgegebenes
, so dass ein vorgegebenes ![]() ein Palindrom ist.
ein Palindrom ist.
Die nachfolgende Auflistung zeigt die Folge der zu den Zahlen ![]() gehörenden minimalen Basen
gehörenden minimalen Basen ![]() :
:
(121) 
Für viele der hier aufgelisten minimalen Basen ist das resultierende Palindrom nur schwach, hat also in der Basis-![]() -Darstellung nur zwei Ziffern bzw. ist nur vom Grade 2. Die Frage nach der minimalen Basis mit der Eigenschaft Grad
-Darstellung nur zwei Ziffern bzw. ist nur vom Grade 2. Die Frage nach der minimalen Basis mit der Eigenschaft Grad ![]() liegt daher nahe. Das ist zugleich die Frage nach der minimalen Basis, so dass das entsprechende Palindrom echt ist, also aus mindestens
liegt daher nahe. Das ist zugleich die Frage nach der minimalen Basis, so dass das entsprechende Palindrom echt ist, also aus mindestens ![]() Ziffern besteht.
Ziffern besteht.
Wir listen für die ersten ![]() Zahlen die Folge der zugehörigen Basen mit Grad
Zahlen die Folge der zugehörigen Basen mit Grad ![]() auf und notieren
auf und notieren ![]() , falls es eine solche Basis nicht gibt.
, falls es eine solche Basis nicht gibt.
(122) 
Schließlich ist noch die Folge der kleinsten Zahlen, die keine echten Palindrome sind von Interesse. Die ersten davon sind:
(123) 
Für diese Zahlen Z existieren somit keine Basen ![]() , so dass
, so dass ![]() als ein echtes Palindrom, also als ein Palindrom mit mindestens
als ein echtes Palindrom, also als ein Palindrom mit mindestens ![]() Ziffern darstellbar ist.
Ziffern darstellbar ist.


