Wir diskutieren im Folgenden spezielle Eigenschaften von Monomen der Art \(y = ax^n\) mit \(n \in \mathbb{N}, n\ge 2 \) bzw. \(y = ax^t\) mit \(t \in \mathbb{R}, t\ge 2 \), insbesondere betrachten wir die Kurvenkrümmung und den Krümmungsradius. In Abbildung 1 sind exemplarisch die drei Monome \(y = x^4\), \(y = x^{10}\) und \(y = x^{20}\) mit der Lage der entsprechenden minimalen Krümmungskreisen dargestellt.
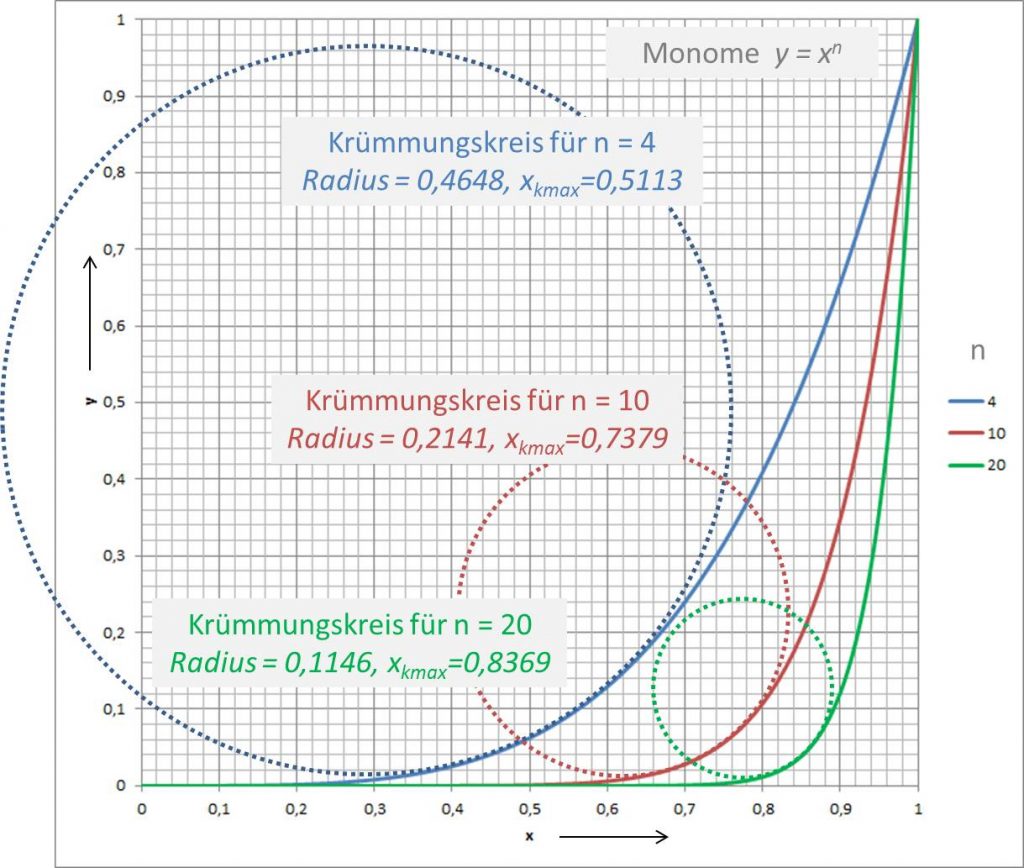
Abbildung 1
Die Kurve des Monoms \(y = ax^n \) hat ihre maximale Krümmung \(k\) an der Position
\begin{equation} \begin{array}{l} x = x^{(n)}\mid_{k=\text{max}} &= \pm \, \sqrt[{2n-2}]{\dfrac{n-2}{a^2n^2(2n-1)}} \\ &= \pm \, {\left({\dfrac{1}{an}\sqrt{\dfrac{n-2}{2n-1}}}\right)}^{\frac{1}{n-1}} \end{array} \end{equation}
Die Krümmung \(k\) selbst nimmt den Wert
\begin{align} \begin{array}{l} k &= \dfrac{an(n-1)x^{n-2}}{\left(1+a^2n^2x^{2n-2}\right)^{\frac{3}{2}}} \\ &= \sqrt{3\dfrac{n-2}{n-1}}\dfrac{2n-1}{9x} \end{array} \end{align}
an, wobei hier der obige positive Wert von \(x\) einzusetzen ist.
Im Grenzfall \( n = 2 \) ist \(x=0\) und die Krümmung nimmt den Wert \( k=2a \) an. Für das Monom \(y = x^2\) ergibt sich also die maximale Krümmung im Punkt \(x=0 \) mit \( k=2 \) und somit der minimale Krümmungsradius zu \( r=\frac{1}{2} \).
Ohne Bezug auf \(x\) kann man die Krümmung direkt mit der folgenden Formel bestimmen
\begin{align} \begin{array}{l} k &= \dfrac{2n-1}{9} \sqrt{3\dfrac{n-2}{n-1}} {\left({\dfrac{a^2n^2(2n-1)}{n-2}} \right)}^{\dfrac{1}{2n-2}} \\ &= \dfrac{{\left({{an}}\sqrt{{(2n-1)}^{{2n-1}} {(n-2)}^{{n-2}}} \right)}^{\dfrac{1}{n-1}}}{{3} \sqrt{3(n-1)}} \end{array} \end{align}
Mit wachsendem Exponenten \( n \) wandern die Punkte maximaler Krümmung auf den Kurven \(y = x^n\) von \((x,y) = (0,0)\) für \( n = 2 \) bis \((x,y)=(1,0)\) für \( n \to \infty \). Der Zusammenhang ist in Abbildung 2 dargestellt.
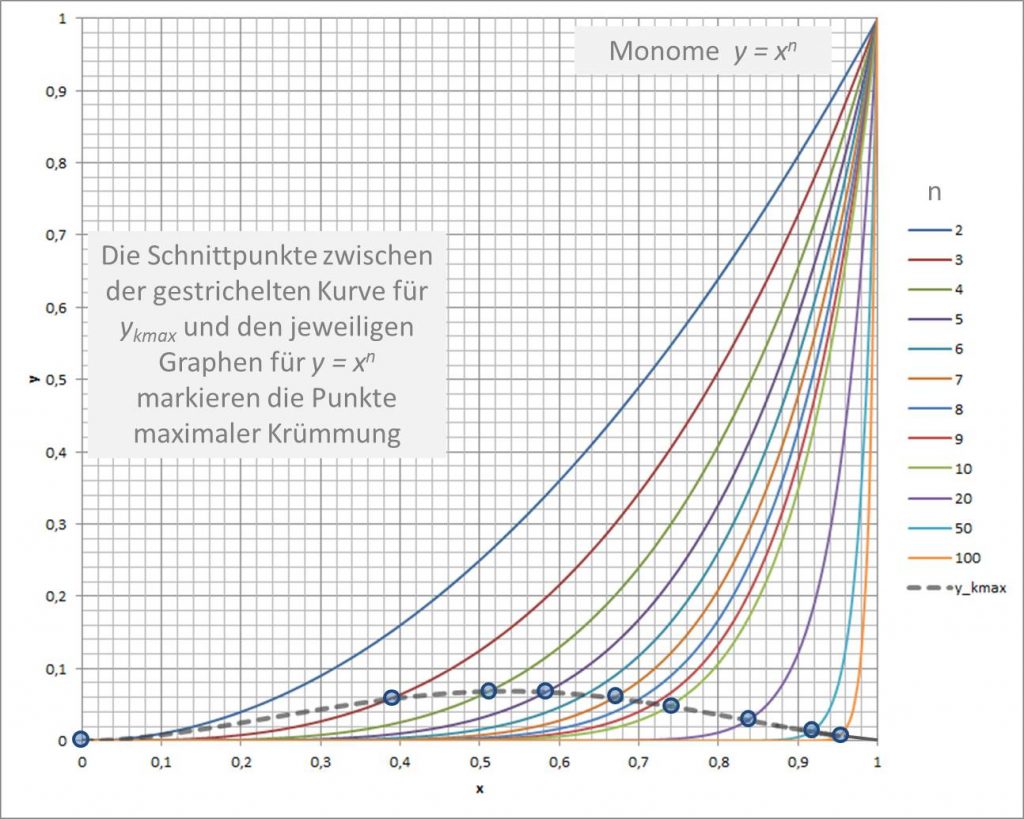
Abbildung 2
Die Trajektorie des Punktes der maximalen Krümmung \((x_{k_{\text{max}}}, y_{k_{\text{max}}}) \) der Kurve \(y = x^t\) bei Variation von \(t\) von \(t=2\) bis \(t=\infty\) für positive Werte von \(x\) ist in der nachfolgenden Grafik vergrößert dargestellt.
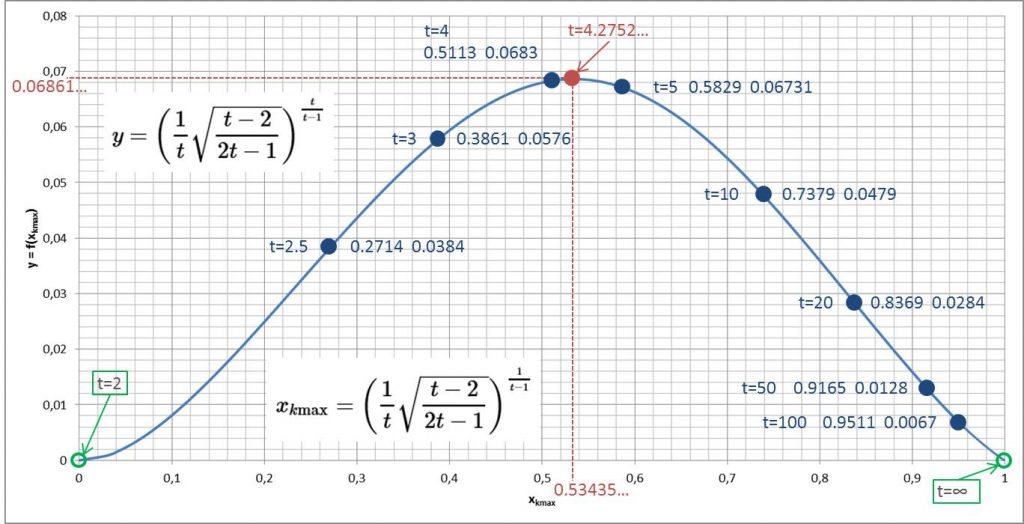
Abbildung 3
Für den Exponenten \(t=4.275228241082256\dots\) nimmt \( y_{k_{\text{max}}} \) den maximalen Wert von \( 0.0686107444107495\dots \) an, zugleich ist \( x_{k_{\text{max}}}= 0.53434968313776\dots \).
Interessant ist die Frage nach dem Verhalten dieses Graphen am linken und am rechten Rand des Definitionsbereichs. Betrachten wir zunächst einmal die Umgebung von \(t=2\) und setzen hierfür \(\tau :=t-2\):
\begin{align} x_{k_{\text{max}}} &= \frac{{\tau}^{\frac{1}{2}}}{2\sqrt{3}}\left( 1 + \frac{\log(1728)-5-3\log(\tau)}{6}\tau + \text{O}{\left({\tau}^{2}\log(\tau)\right)}\right) \\ y_{k_{\text{max}}} &= \frac{{\tau}}{12}\left( 1 + \frac{\log(1728)-10-\log(\tau)}{6}\tau + \text{O}{\left({\tau}^{2}\log(\tau)\right)}\right) \end{align}
Demnach gilt also für kleine \(\tau =t-2 \) die Näherungsformel
\begin{align} y_{k_{\text{max}}} \approx x_{k_{\text{max}}}^2 \end{align}
Tatsächlich erhalten wir für die Ableitung
\begin{align} \begin{array}{l} \dfrac{\text{d}{y_{k_{\text{max}}}}}{\text{d}{x_{k_{\text{max}}}}} &= \dfrac{\dot{y}_{k_{\text{max}}}}{\dot{x}_{k_{\text{max}}}} \\ &= \dfrac{{\tau}^{\frac{1}{2}}}{\sqrt{3}} + \text{O}{\left({\tau}\log(\tau)\right)} \\ &= 2{x_{k_{\text{max}}}} + \text{O}{\left({x_{k_{\text{max}}}^2}\right)} \end{array} \end{align}
für \(\tau =t-2 \to 0+\).
Aus den beiden obigen Approximationen folgt zwanglos
\begin{align} \lim_{t \rightarrow 2+}{\frac{x_{k_{\text{max}}} }{\sqrt{t-2}}} &= \frac{1}{2\sqrt{3}} \\ \lim_{t \rightarrow 2+}{\frac{y_{k_{\text{max}}} }{t-2}} &= \frac{1}{12}\end{align}
Am anderen Ende, also für \(t \to \infty \), geht \( y_{k_{\text{max}}} \) ebenfalls gegen \(0\,\)während \( x_{k_{\text{max}}} \to 1\) strebt. Der Graph erweckt dabei den Anschein, als ob die Trajektorie die \(x\)-Achse unter einem positiven Winkel scheiden würde. Das ist indes nicht zutreffend. Stattdessen haben wir in diesem Fall die Näherung
\begin{align} \frac{y_{k_{\text{max}}}}{1 – x_{k_{\text{max}}}} \approx -\frac{1}{\sqrt{2}\log(y_{k_{\text{max}}})}\end{align}
Demnach gilt also \(\frac{\text{d}{y_{k_{\text{max}}}}}{\text{d}{x_{k_{\text{max}}}}} \to 0 \) für \(t \to \infty \).
Generell beschreiben die beiden Näherungsformeln
\begin{align} x_{k_{\text{max}}} &= 1 – \frac{\log(2) + 2\log(t)}{2 t} + \frac{\left(\log(2) + 2\log(t) – 2\right)^2 – 10}{8 t^2} + \text{O}{\left(t^{-3}\log(t)\right)} \\ y_{k_{\text{max}}} &= \frac{1}{\sqrt{2}\,t} – \frac{3+\log(4) + 4\log(t)}{4\sqrt{2}\,t^2} + \text{O}{\left(t^{-3}\log(t)\right)} \end{align}
das Verhalten des Graphen von \(\left(x_{k_{\text{max}}}(t),\, y_{k_{\text{max}}}(t)\right) \) für große Exponenten \(t \to \infty \). Insbesondere folgt hieraus
\begin{align} \lim_{t\rightarrow \infty}{t\,y_{k_{\text{max}}}(t)} = \frac{1}{\sqrt{2}} \end{align}
sowie
\begin{align} \lim_{x_{k_{\text{max}}}\rightarrow 1-}\frac{y_{k_{\text{max}}}\log(y_{k_{\text{max}}})}{1 – x_{k_{\text{max}}}} = -\frac{1}{\sqrt{2}} \end{align}
Kommen wir nun zum Krümmungsradius \(r\). Aus (5) resultiert unmittelbar die folgende Formel
\begin{align} r = \frac{1}{k} = \frac{{3} \sqrt{3(n-1)}}{ {\left({{an}}\sqrt{{(2n-1)}^{{2n-1}} {(n-2)}^{{n-2}}} \right)}^{\frac{1}{n-1}}} \end{align}
In Abbildung 4 ist der Verlauf \(r=r(t)\) für \(a=1\) dargestellt.
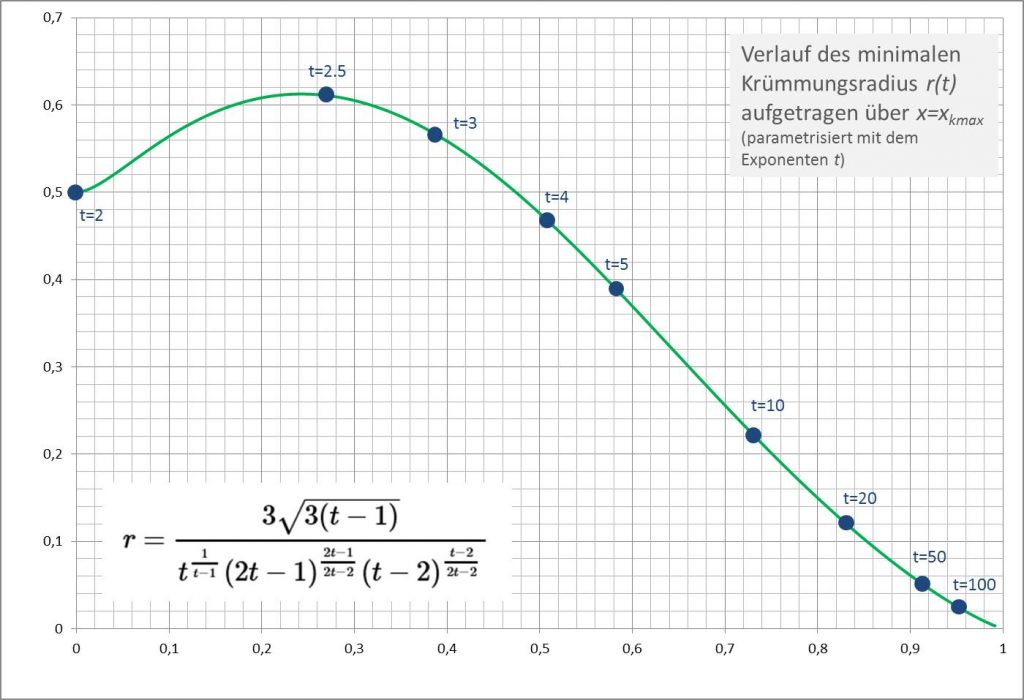
Abbildung 4
Es fällt auf, dass der minimale Krümmungsradius eines Monoms \(y = x^t\) für Exponenten \(t \gt 2 \) zunächst einmal über den initialen Wert von \(r=\frac{1}{2} \) hinauswächst und bei \(t \approx 2.4\) ein Maximum erreicht. Der Ausgangswert wird erst wieder bei \(t\approx 3.6 \) (genauer: \(t =3.6303342714085 \dots\)) unterschritten. Das verwundert! Intuitiv hätte man mit wachsendem Exponenten eine ebenfalls wachsende maximale Krümmung auf der Kurve \(y = x^t\) und damit einen sich gleichmäßig reduzierenden minimalen Krümmungsradius erwartet.
Ein genauerer Wert für den Exponenten, bei dem das Maximum des minimalen Krümmungsradius erreicht wird, ist \(t =2.41028507349901 \dots\). Der zugehörige Krümmungsradius ist \(r =0.61261263904161 \dots\). Dazu korrespondieren \( x_{k_{\text{max}}}= 0.24295265668411 \dots\) und \( y_{k_{\text{max}}}=0.03303178254774 \dots\) als die entsprechenden \(x\)- und \(y\)-Werte des Punktes der maximalen Krümmung auf der Kurve des Monoms \(y=x^t\).
Auch hier kann man wieder nach dem Verhalten für kleine und große Exponenten \(t\) fragen.
Bei kleinen Exponenten \( t = 2+\tau \) erhalten wir die folgende Näherung
\begin{align} r = \frac{1}{2} + \frac{\log(12) – 2 -\log(\tau)}{4}\tau +r_2(\tau){\tau}^2 + \text{O}{\left(\tau^{3}\log({\tau})\right)} \end{align}
wobei
\begin{align} r_2(\tau) = \frac{3{(\log(\frac{\tau}{3}))}^2+12\log(\frac{\tau}{3})(4-\log(8))-6(1+\log(4))\log(2)+31}{48} \end{align}
In Abbildung 4 ist der Graph von \( r(t) = r(x_{k_{\text{max}}}(t)) \) dargestellt. In der Nähe des Punktes \(x = x_{k_{\text{max}}} = 0\) erhält man für die Steigung der Kurve
\begin{align} \frac{\text{d}{r(t)}}{\text{d}{x_{k_{\text{max}}}}} &= \frac{\dot{r}(t)}{\dot{x}_{k_{\text{max}}}} \notag \\ &= \sqrt{3}{\left(\log(12)-1-\log(\tau)\right)}{\tau}^{\frac{1}{2}} + \text{O}{\left({\tau}\log(\tau)\right)} \\ \notag &= -6\left(3+2\log({x_{k_{\text{max}}}})\right){x_{k_{\text{max}}}} + \text{O}{\left({x_{k_{\text{max}}}^2}\right)} \end{align}
Demnach haben wir also \(\frac{\text{d}{r(x_{k_{\text{max}}}(t))}}{\text{d}{x_{k_{\text{max}}}}(t)} \to 0 \) für \(t \to 2+\) bzw. für \( x_{k_{\text{max}}} \to 0+\).
Aus der vorstehenden Näherungsformel zu \(\frac{\text{d}{r(t)}}{\text{d}{x_{k_{\text{max}}}}} \) ergibt sich mittels Integration die folgende Abschätzung für den Krümmungsradius \(r\) in Abhängigkeit von \({x_{k_{\text{max}}}}\)
\begin{align} r \approx \frac{1}{2} -6\left(1+\log({x_{k_{\text{max}}}})\right) x_{k_{\text{max}}}^2 \end{align}
Zum gleichen Ergebnis gelangt man durch den direkten Vergleich der oben formulierten Näherungen für \({x_{k_{\text{max}}}}\) und \(r\). Für \({x_{k_{\text{max}}}} \lt 0.38\) (das ist zutreffend für Exponenten \(t \lt 3\)) bleibt der Schätzfehler unterhalb von \( \left| \Delta r \right| = 0.1 \), für \({x_{k_{\text{max}}}} \le 0.34\) (das ist zutreffend für Exponenten \(t \le 2.77\)) ist \( \left| \Delta r \right| < 0.04 \).
Aus dem Obigen resultieren die beiden Grenzwerte
\begin{align} \lim_{t\rightarrow 2+}\frac{r(t)-\frac{1}{2}}{(t-2)\log(t-2)} = -\frac{1}{4} \end{align}
und
\begin{align} \lim_{x_{k_{\text{max}}}\rightarrow 0+}\frac{r(x_{k_{\text{max}}})-\frac{1}{2}}{x_{k_{\text{max}}}^2\log({x_{k_{\text{max}}}})} = -6\end{align}
Nun zur Analyse für \( t \to \infty \). Hier erhalten wir die Approximation
\begin{align} r = \frac{3\sqrt{3}}{2t} \left( 1 + \frac{2-\log(2t)}{2t} +\text{O}{\left(t^{-2}\log(t)\right)}\right) \end{align}
Damit ist also
\begin{align} \lim_{n\rightarrow \infty}{n\,r} = \frac{3\sqrt{3}}{2} \end{align}
In Abbildung 5b sind beide Achsen logarithmisch dargestellt, hier erkennt man den Charakter der vorstehend formulierten Näherung unmittelbar.
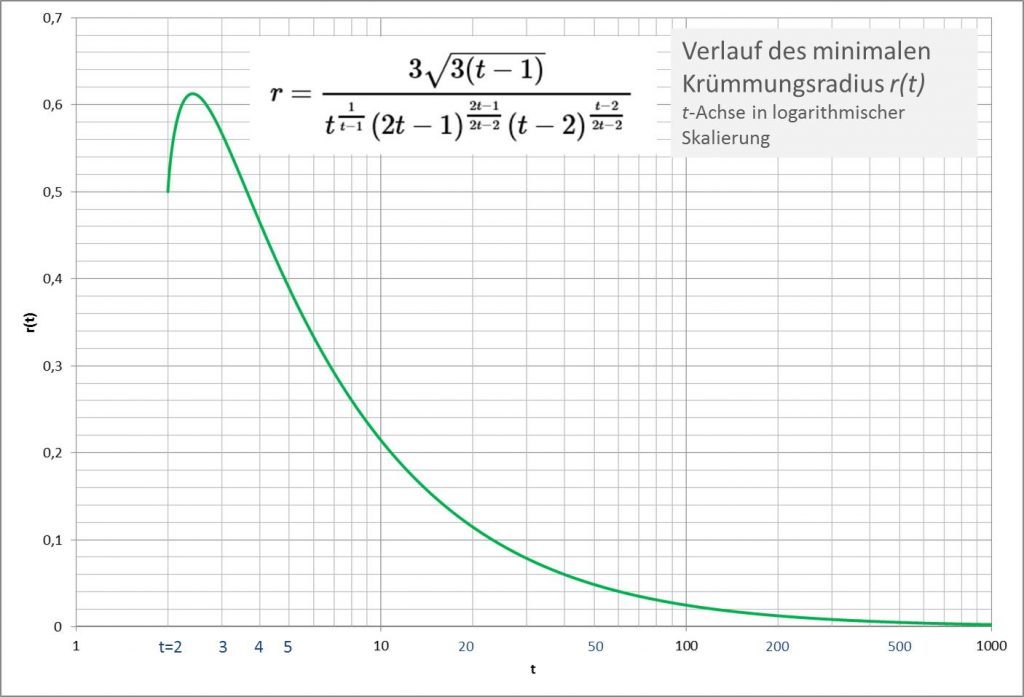
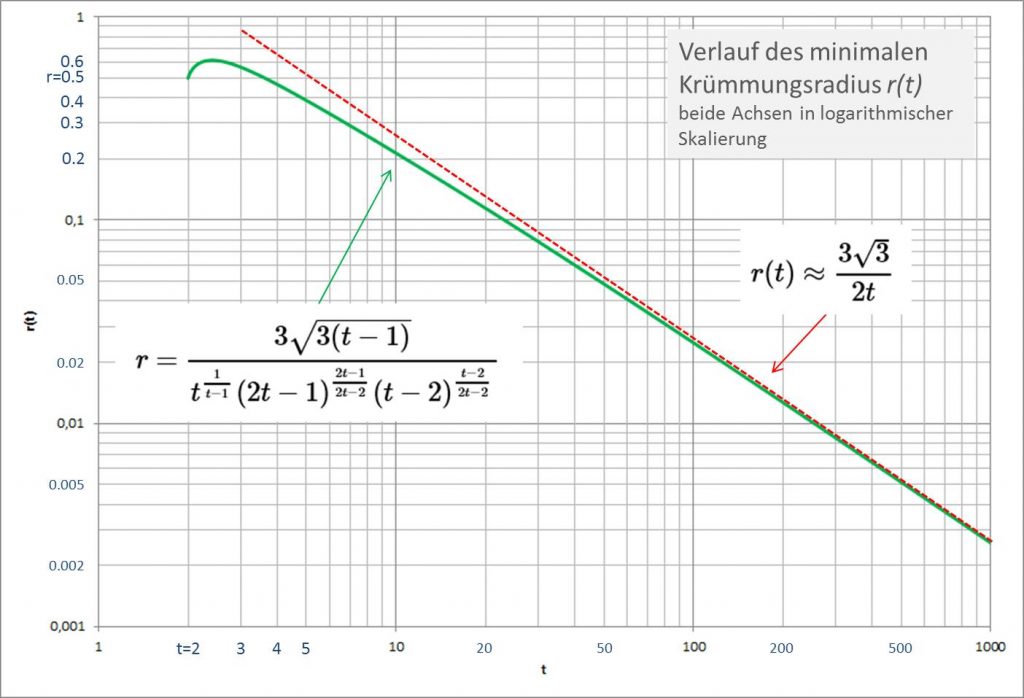
Abbildung 5a/b
Im folgenden betrachten wir die Trajektorie der Krümmungskreismittelpunkte \( (x_0, y_0) \). Die Konstruktion der entsprechenden Punkte ist in Abbildung 6 am Beispiel des Exponenten \(n = t = 10 \) dargestellt.
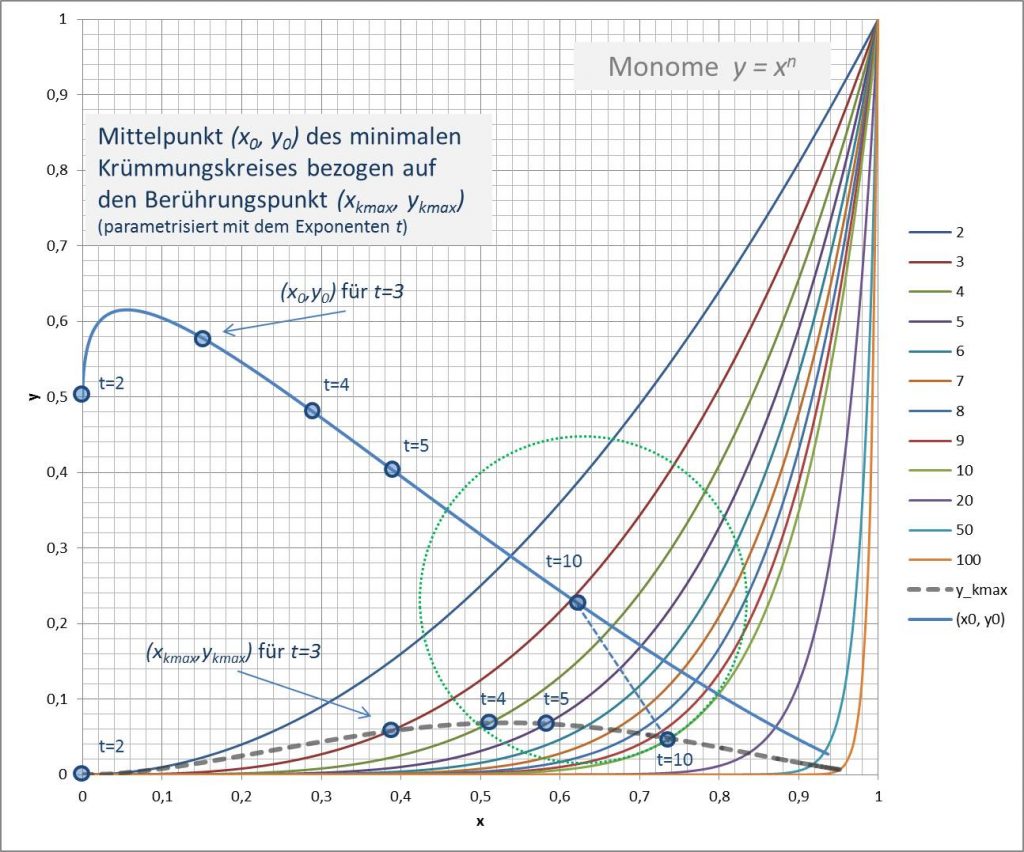
Abbildung 6
Für zwei weitere Beispiele von Krümmungskreisen bezogen auf die Exponenten \(n = 5\) und \( n=20 \) s. Abbildung 7.
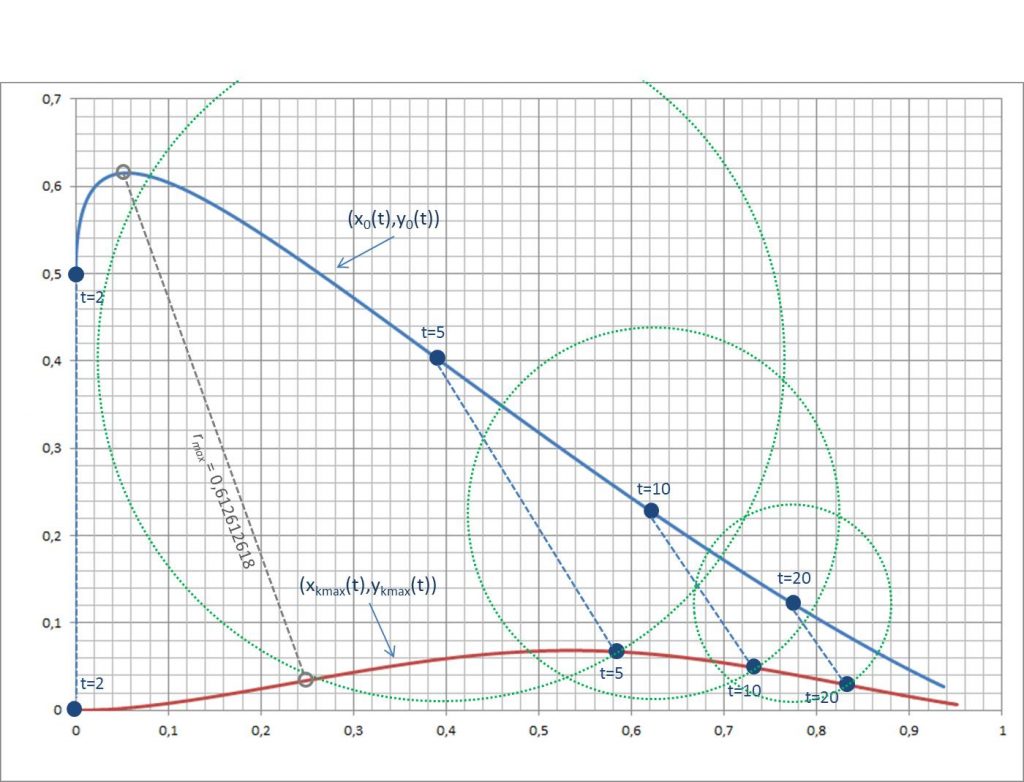
Abbildung 7
Die Positionen \( (x_0, y_0) \) werden aus den \( (x_{k_{\text{max}}}, y_{k_{\text{max}}}) \) und dem entsprechenden Krümmungsradius \( r \) folgendermaßen berechnet:
\begin{align} x_0 &= x_{k_{\text{max}}}-\sqrt{\frac{t-2}{3(t-1)}}\cdot r \\ y_0 &= y_{k_{\text{max}}}+\sqrt{\frac{2t-1}{3(t-1)}}\cdot r \end{align}
Die Näherungsausdrücke für \(\tau =t-2 \to 0+\) sind
\begin{align} x_{0} = &\frac{{\tau}^{\frac{3}{2}}}{3 \sqrt{3}} + \text{O}{\left(\tau^{\frac{5}{2}}\right)} \\ y_{0} = &\frac{1}{2} + \frac{\log(1728)-7 -3\log(\tau)}{12}\tau + b_2(\tau){\tau}^2 + \text{O}{\left(\tau^{3}\log({\tau})\right)} \end{align}
wobei
\begin{align} b_2(\tau) = \frac{9\,{(\log(\frac{\tau}{3}))}^2+36\log(\frac{\tau}{3})(4-\log(8))+4\log(\tau)-18(1+\log(4))\log(2)+96}{144} \end{align}
Aus den vorstehenden Ausdrücken folgen unmittelbar die beiden Limites
\begin{align} \lim_{t \rightarrow 2+}{\frac{x_0}{{(t-2)}^{\frac{3}{2}}}} &= \frac{1}{3\sqrt{3}} \\ \lim_{t \rightarrow 2+}{\frac{y_0 – \frac{1}{2}}{(t-2)\log(t-2)}} &= -\frac{1}{4}\end{align}
Für kleine Werte von \( x_0 \) erhalten wir zudem die folgende Approximation
\begin{align} y_0 \approx \frac{1}{2} + \frac{\log(64)-7-2\log(x_0)}{4}\,x_0^{\frac{2}{3}} \end{align}
und somit den Limes
\begin{align} \lim_{x_0 \rightarrow 0+}\frac{y_0 – \frac{1}{2}}{x_0^{\frac{2}{3}}\log(x_0)} = -\frac{1}{2} \end{align}
Weiter erhält man für \( t \to \infty \)
\begin{align} x_{0} = &1 – \frac{3+\log(2)+2\log(t)}{2t} + \frac{c_2(t)}{t^2} + \text{O}{\left(t^{-3}\log(t)\right)} \\ y_{0} = &\frac{2\sqrt{2}}{t} + \frac{(6 -4\log(2)-5\log(t))\sqrt{2}}{4t^2} + \text{O}{\left(t^{-3}\log(t)\right)} \end{align}
wobei
\begin{align} c_2(t) = \frac{{(\log(2t^2) – 2)}^2 – 6\log(2t)}{8}-2 \end{align}
Die Grenzwerte für \( t\rightarrow \infty \) bzw. \( x_0 \rightarrow 1- \) ergeben sich zu
\begin{align} \lim_{t\rightarrow \infty}{t\,y_0(t)} = 2\sqrt{2} \end{align}
sowie
\begin{align} \lim_{x_0 \rightarrow 1-}\frac{y_0\log(y_0)}{1 – x_0} = -2\sqrt{2} \end{align}
Interessant ist noch die Betrachtung des Verlaufs des Winkels \(\alpha\) der Steigung der Kurve \(y=x^t\) am Punkt der maximalen Krümmung. Für \(n=t=2\) ist dieser Winkel \(\alpha = 0^{\circ} \). Mit wachsendem Exponenten wird der Winkel steiler und wächst schnell zu Werten über \(30^{\circ} \) hin. Vom Augenschein her (z.B. von Abbildung 6) ist es zunächst aber dennoch unklar, wie sich der Winkel bei größeren Werten von \(t\) verhält. Wir brauchen die Ableitung von \(y=x^t\) für \(x = x_{k_{\text{max}}}\) und greifen dazu auf Formel (1) zurück.
\begin{align} \begin{array}{l} \dfrac{\mathrm{d}{y}}{\mathrm{d}{x}}{\mid_{x = x_{k_{\text{max}}}}} &= t\cdot x^{t-1} \\ &={\sqrt{\dfrac{t-2}{2t-1}}} \end{array} \end{align}
Abbildung 8 zeigt die Steigung der Kurve \(y=x^t\) am Punkt der maximalen Krümmung in Abhängigkeit von \(t\).
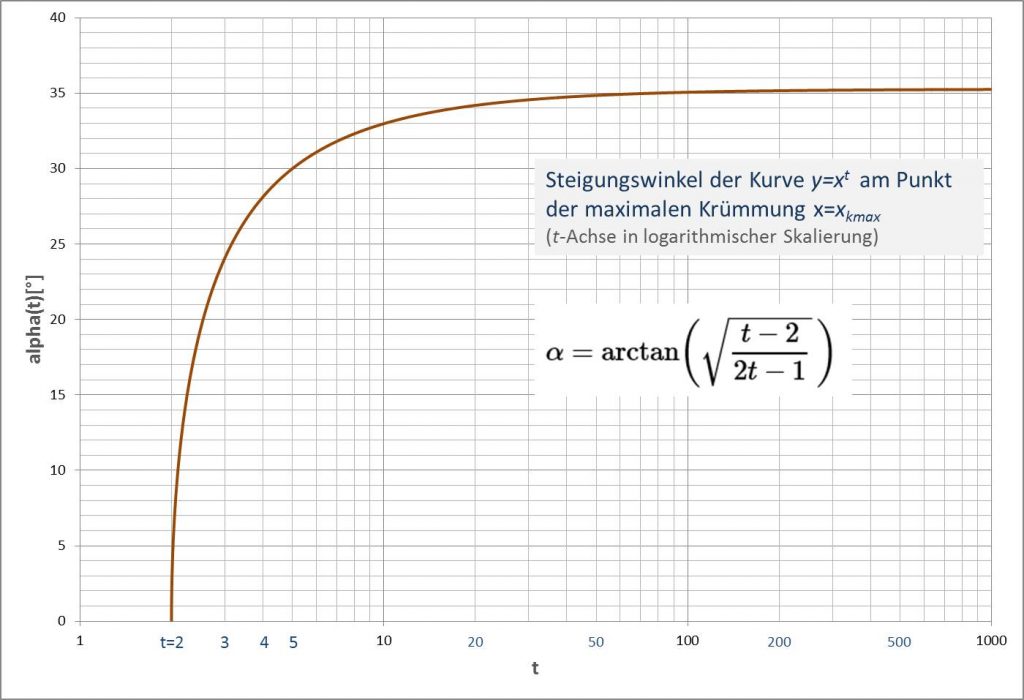
Abbildung 8
Abbildung 9 zeigt den Verlauf des Steigungswinkels in Abhängigkeit von der Position \(x_{k_{\text{max}}} \) und parametrisiert mit \(t\).
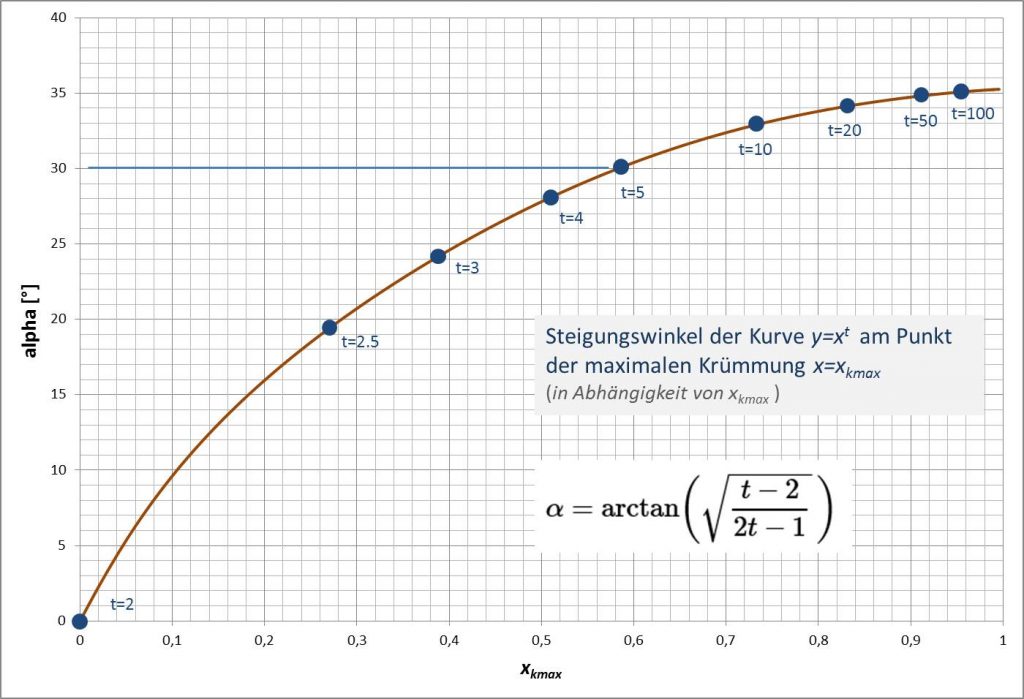
Abbildung 9
Für kleine Werte von \(\tau =t-2 \) ergibt sich für \(y^{\prime} = \frac{\mathrm{d}{y}}{\mathrm{d}{x}}{\mid_{x = x_{k_{\text{max}}}}}\) die folgende Näherungsformel
\begin{align} y^{\prime}{\mid_{x = x_{k_{\text{max}}}}} &= \frac{{\tau}^{\frac{1}{2}}}{\sqrt{3}}\left( 1\, – \frac{\tau}{3} + \frac{\tau^2}{6} + \text{O}{\left({\tau}^{3}\right)}\right) \end{align}
Die Steigung \( y^{\prime}{\mid_{x = x_{k_{\text{max}}}}}(t) \) ist für \(t=2\) gleich \(0\), steigt mit \(t\) aber rasch an. Betrachtet man die Abhängigkeit von der Position \(x_{k_{\text{max}}}\) der maximalen Krümmung (s. Abbildung 9), so findet man für \(x_{k_{\text{max}}} \rightarrow 0 \) den Näherungsausdruck
\begin{align} y^{\prime\prime}{(x)}{\mid_{x = x_{k_{\text{max}}}}} = \frac{\mathrm{d}{y\prime}}{\mathrm{d}{x}}{\mid_{x = x_{k_{\text{max}}}}} = 2 + \text{O}{\left({x_{k_{\text{max}}}}\right)} \end{align}
und damit auch \( \lim_{x_{k_{\text{max}}} \rightarrow 0}{y^{\prime\prime}{(x)}{\mid_{x = x_{k_{\text{max}}}} }} = 2 \). Der Steigungswinkel \(\alpha\) wächst daher für kleine \(x_{k_{\text{max}}}\) anfänglich mit eine Rate von \(\frac{\Delta\alpha}{\Delta{x_{k_{\text{max}}}}} \approx 2 \cdot \frac{180}{\pi} \approx 114^{\circ}\). In Abbildung 9 kann man das gut erkennen.
Für \(t \rightarrow \infty \) lautet die Approximation
\begin{align} y^{\prime}{\mid_{x = x_{k_{\text{max}}}}} &= \frac{1}{\sqrt{2}}\left( 1\, – \frac{3}{4\, t} + \frac{21}{t^2} + \text{O}{\left({t}^{-3}\right)}\right) \end{align}
Demnach strebt die Steigung der Kurve \(y=x^t\) am Punkt der maximalen Krümmung für \(t \rightarrow \infty \) gegen den Wert \(\frac{1}{\sqrt{2}}\), also
\begin{align} \lim_{t\rightarrow \infty}{y^{\prime}{\mid_{x = x_{k_{\text{max}}}}}(t)} = \frac{1}{\sqrt{2}} \end{align}
Für den Steigungswinkel heißt das
\begin{align} \begin{array} {l} \displaystyle \lim_{t\rightarrow \infty}{\alpha(t)} &= \arctan\left(\dfrac{1}{\sqrt{2}}\right) \\ &= 35.264389682754654315377000330019^{\circ} \end{array} \end{align}
Der Verbindungsstrahl zwischen dem Mittelpunkt \( (x_0, y_0)\) des Krümmungskreises und dem zugeordneten Punkt der maximalen Krümmung \( (x_{k_{\text{max}}} , y_{k_{\text{max}}} \) steht senkrecht über der Kurve des Monoms \(y=x^t\)
Der Winkel \(\phi\) der Normalen auf der Kurve \(y=x^t\) am Punkt der maximalen Krümmung ergibt sich aus dem Steigungswinkel \( \alpha\) zu\(\phi = \alpha + 90^{\circ} \). Für \(n=t=2\) ist dieser Winkel \(\phi = 90^{\circ} \). Mit wachsendem Exponenten wird der Winkel flacher und neigt sich schnell zu Werten über \(110^{\circ} \) hin. Bei dem Exponenten \(t=5\) ist der Normalenwinkel genau \(120^{\circ} \). In Abbildung 10 sind die Positionen der Punkte maximaler Krümmung \( (x_{k_{\text{max}}} , y_{k_{\text{max}}}) \) (rote Kurve) zusammen mit den Mittelpunkten \( (x_0, y_0)\) der entsprechenden Krümmungskreise (blaue Kurve) parametrisiert mit dem Exponenten \(t\) aufgetragen. Für einige ausgewählte Parameter \(t\) sind die Verbindungsstrecken \( \overline{(x_{k_{\text{max}}} , y_{k_{\text{max}}}) (x_0, y_0)}\) gezeichnet (gestrichelte blaue Linien). Zusätzlich sind für \(t=2,3,5,10\) und \(t=\infty\) die Winkel der Normalen auf der Kurve \(y=x^t\) explizit dargestellt.
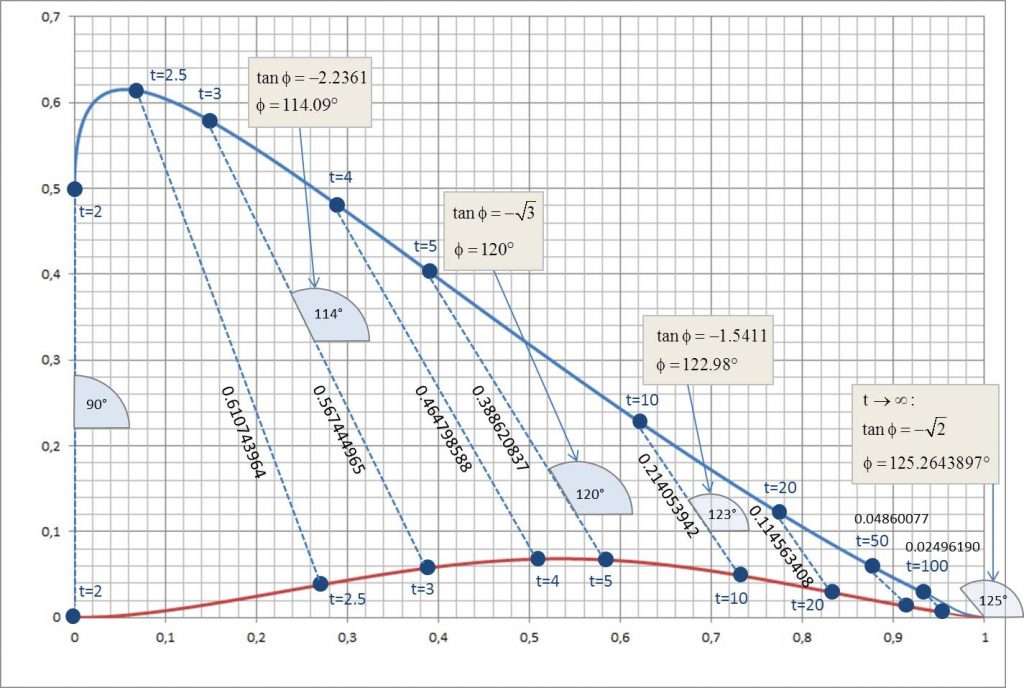
Abbildung 10
Formal folgt aus Formel (38)
\begin{align} \begin{array}{l} \tan \phi &= -\dfrac{1}{y^{\prime}{\mid_{x = x_{k_{\text{max}}}}}} \\ &=-{\sqrt{\dfrac{2t-1}{t-2}}} \end{array} \end{align}
Damit erhält man für die Näherungsausdrücke wie oben
\begin{align} \tan \phi &= -{\sqrt{3}}\,{\tau}^{-\frac{1}{2}}\left( 1 + \frac{\tau}{3} – \frac{\tau^2}{18} + \text{O}{\left({\tau}^{3}\right)}\right) \quad \text{für } \tau=t-2 \rightarrow 0+ \end{align}
\begin{align} \tan \phi &= -\sqrt{2}\left( 1 + \frac{3}{4\, t} – \frac{327}{16\,t^2} + \text{O}{\left({t}^{-3}\right)}\right) \quad \text{für } t \rightarrow \infty \end{align}
und somit auch den Grenzwert
\begin{align} \begin{array} {l} \displaystyle \lim_{t\rightarrow \infty}{\phi(t)} &= \arctan\left({-\sqrt{2}}\right) \\ &= 125.264389682754654315377000330019^{\circ} \end{array} \end{align}
In dem „unscheinbaren“ Winkel \(\phi\) stecken gewissermaßen alle Informationen über die fraglichen Größen \(t\), \( x_{k_{\text{max}}}\), \(y_{k_{\text{max}}}\), \( x_0\), \(y_0\) und \( r \): Aus \(\phi\) lassen sich alle anderen Werte berechnen, denn Formel (44) ist einfach nach \(t\) auflösbar. Es gilt
\begin{align} \begin{array}{l} t &= \dfrac{1 – 2 \tan^2 \phi }{2 – \tan^2 \phi } \\ &= 2 + \dfrac{3}{\tan^2 \phi \, – 2} \end{array} \end{align}
wobei \(\phi\) im Bereich zwischen \(\frac{\pi}{2}\) und \(\frac{\pi}{2} + \arctan {\frac{1}{\sqrt{2}}} = 2,186276\dots\) liegt (das entspricht dem obigen Wert für \( \lim_{t\rightarrow \infty}{\phi(t)}) \). – Hat man also den Winkel \(\phi\) und die Lage eines gegebenen Punkts \((x, y)\) als Platzhalter für den Mittelpunkt des Krümmungskreises oder den Punkt maximaler Krümmung eines zunächst noch unbekannten Monoms, so können daraus die weiteren Größen und Positionen direkt berechnet werden.
Wenn wir nun für \( t \to \infty \) die Approximationen für \( x_{k_{\text{max}}}\), \(y_{k_{\text{max}}}\), \( x_0\), \(y_0\) und \( r \) im Zusammenhang betrachten, erkennen wir die folgenden Beziehungen
\begin{align} y_{k_{\text{max}}} \approx \frac{1}{\sqrt{2}\,t} \end{align}
\begin{align} x_0 \approx x_{k_{\text{max}}} – \frac{3}{2\,t} \approx x_{k_{\text{max}}} – \frac{3\sqrt{2}}{2}\cdot y_{k_{\text{max}}} \end{align}
\begin{align} y_0 \approx \frac{2\sqrt{2}}{t} \approx 4\cdot y_{k_{\text{max}}} \end{align}
\begin{align} r \approx \frac{3\sqrt{3}}{2\,t} \approx \frac{3\sqrt{6}}{2}\cdot y_{k_{\text{max}}} \end{align}
Wegen Formel (10) können wir das ergänzen um
\begin{align} \begin{array} {l} 1 – x_0 &\approx 1 – x_{k_{\text{max}}} + \dfrac{3}{2\,t} \\ &\approx -\sqrt{2}\,{y_{k_{\text{max}}}\log(y_{k_{\text{max}}})} + \dfrac{3\sqrt{2}}{2}\cdot y_{k_{\text{max}}} \\ &\approx \dfrac{3 – 2\log(y_{k_{\text{max}}})}{\sqrt{2}} \cdot y_{k_{\text{max}}} \end{array} \end{align}
Der Abstand \(\Delta y_u \) der Peripherie des Krümmungskreises von der \(x\)-Achse ergibt sich somit zu
\begin{align} \begin{array} {l} \Delta y_u = y_0 – r &\approx \dfrac{4\sqrt{2}\, – 3\sqrt{3}}{2} \cdot \dfrac{1}{t} \\ &\approx \left( 4\, – \dfrac{3\sqrt{6}}{2}\right)\cdot y_{k_{\text{max}}} \end{array} \end{align}
Analog folgt für Abstand \(\Delta x_r \) der Peripherie des Krümmungskreises von der vertikalen Geraden bei \(y=1\)
\begin{align} \begin{array} {l} \Delta x_r = 1 – x_0 – r &\approx \dfrac{\log(2\,t^2)+3-3\sqrt{3}}{2} \cdot \dfrac{1}{t} \\ & \approx \dfrac{3\, – 3\sqrt{3}\, – 2\log(y_{k_{\text{max}}})}{\sqrt{2}} \cdot y_{k_{\text{max}}} \end{array} \end{align}
Insgesamt erhalten wir in der Situation \( t \to \infty \) in erster Näherung die in Abbildung 11 (Skizze A) dargestellte Konstellation. Ausgehend von der typischen Kurve für \( y=x^t\) und der Position von \( x_{k_{\text{max}}}\) auf der schematischen \(x\)-Achse sind die davon abgeleiteten Werte für \( x_0\), \(y_0\) und \(y_{k_{\text{max}}}\) sowie die daraus resultierenden Positionen der betreffenden Punkte eingetragen. Der Wert von \(r\) ergibt sich als Ergebnis dieser Konstruktion. Wie groß wir \(t\) auch immer wählen, bleiben die Beziehungen zwischen den genannten Größen bis auf marginale, in der erreichbaren Genauigkeit einer Zeichnung gar nicht darstellbaren Änderungen völlig gleich. Der Parameter \(t\) spielt damit also die Rolle des Maßstabsfaktors.
Vorausgesetzt, wir betrachten weiter große \( t \), so können wir die Zusammenhänge sogar ohne jeden Bezug auf den Exponenten schon mit der Referenzgröße \(y_{k_{\text{max}}}\) für \( t \to \infty \) asymptotisch korrekt darstellen (s. Abbildung 11, Skizze B).
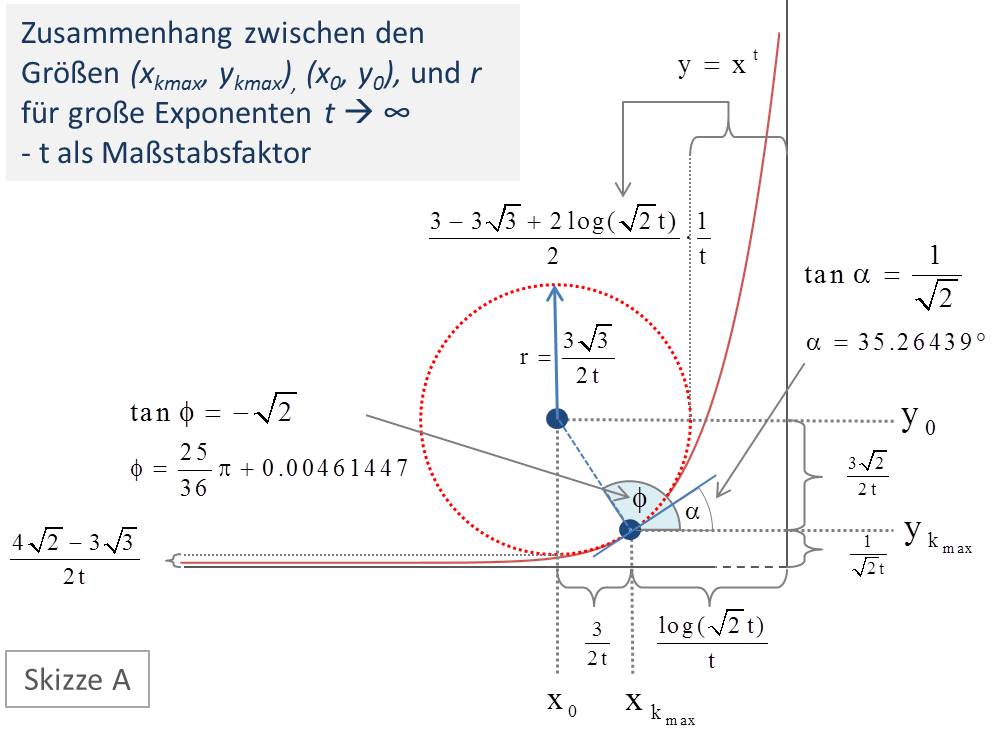
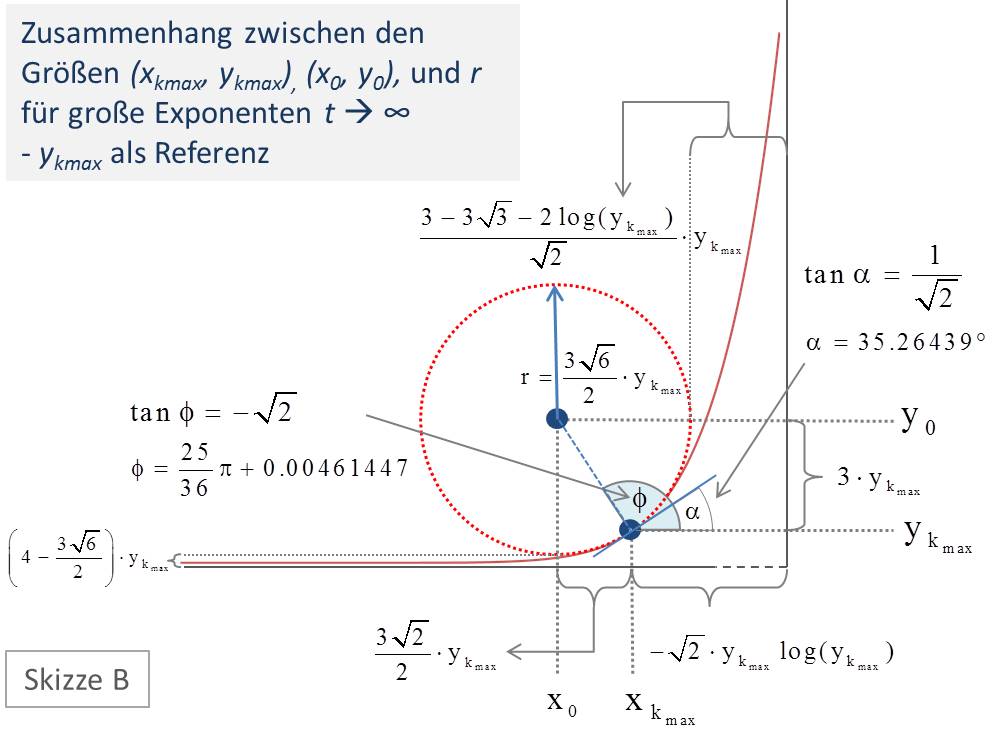
Abbildung 11a/b


